题目描述:
有n个人希望在晚上通过一座桥。在任何时刻,最多只能有两个人在桥上,并且必须要带着手电筒才能通过桥。现在的麻烦是只有一个手电筒,所以必须安排某种顺序,使得手电筒可以被带回去让更多的人过桥(手电筒必须由人带回,不可以从对岸扔过去)。 每个人都有不同的过桥时间,两个人一起过桥所用的时间等于其中较慢的一个。你的任务是要找出能在最短时间内使所有人都过桥的方案。
输入格式:
第一行是一个整数n。 接下来有n行,每一行给出一个人的过桥时间(整数,单位:秒)。
每个人的过桥时间不超过100秒。
输出格式:
输出一行一个数,表示所有人过桥的最短时间。
样例输入:
4
1
2
5
10
样例输出:
17
提示:
40%数据,n<=100。
100%数据,n<=1000。
样例说明:可以先让1和2过桥,然后1回来,让5和10过桥,然后2再回来带1一起过桥,时间为2+1+10+2+2=17。
时间限制: 1000ms
空间限制: 256MB
# include <iostream>
# include <algorithm>
# include <vector>
using namespace std;
vector<int> v(100001);
int fun(int n)
{
if(n == 1)
return v[1];
else if(n == 2)
return max(v[1], v[2]);
else if(n == 3)
return (v[1] + v[2] + v[3]);
else
return fun(n - 2) + min(2*v[1] + v[n] + v[n - 1], 2*v[2] + v[n] + v[1]); //实际上这行代码的意思是分为特定情况下,2*v[1] + v[n] + v[n - 1]是让v[1]来回运手电筒,2*v[2] + v[n] + v[1]这个是让两边小的来回运手电筒,实际上分析下来,第二种既是2*v[2] + v[n] + v[1]这种时间是最短的。
}
int main()
{
int n, m, s;
cin>>n;
for(int i = 1; i <= n; i++)
{
cin>>m;
v[i] = m;
}
sort(v.begin(), v.begin() + n + 1);
s = fun(n);
cout<<s;
return 0;
}
实际上过桥问题就是让两边时间最小的来回过桥运转。
解题思路,首先让最快和次快的过,然后让最快的回来,然后把手电筒给最慢的,最慢的和次慢的过,然后再那头再让次慢的把手电筒给拿过来,以此类推,有周期循环。
以下是解题步骤及例子分析
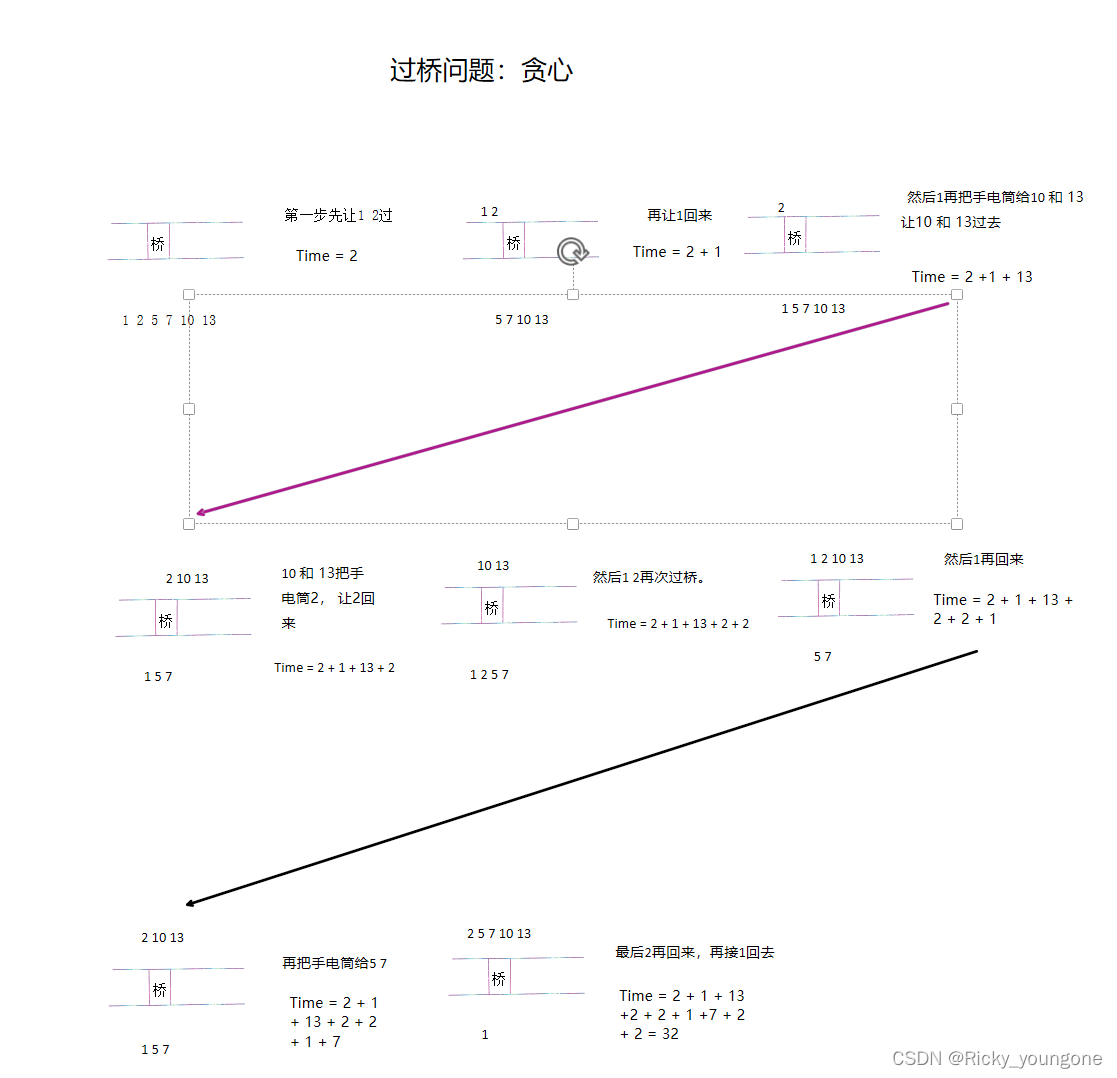




 文章讲述了利用动态规划解决n人过桥问题,找到在有限条件下最短过桥时间的方法。
文章讲述了利用动态规划解决n人过桥问题,找到在有限条件下最短过桥时间的方法。
















 681
681

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








