递归与分治算法练习2

今天聊的还是上次那道题目，老师给了几个标准答案，确实理解起来比我上一个博客所用的方法好多了。
题目：

法一：循环换位算法
分为向前循环和向后循环换位，上一讲的python算法用了列表的切片，你可以看成，一整块数组循环换位了。那么正儿八经的算法就有思路了，我们可以一次一次地循环换位，循环的次数取决于哪边子数组长度更短。只不过交换次数还是比较多的，有点像冒泡算法一类的交换算法。

//向前循环换位
 public static void forward(int a[],int k){
        for (int i = 0; i <=k ; i++) {
            int tmp=a[0];
            for(int j=1;j<a.length;j++){
                a[j-1]=a[j];
            }
            a[a.length-1]=tmp;

        }
    }
    //向后循环换位
    public static void backward(int a[],int k){
        for (int i = a.length-1; i >k; i--) {
            int tmp=a[a.length-1];
            for(int j=a.length-1;j>0;j--){
                a[j]=a[j-1];
            }
            a[0]=tmp;

        }
    }
   
    public static  void change(int a[],int k){
        if(k+1<a.length-1-k)
        {
            forward(a,k);
             //判断左右子数组的长度大小
        }
        else {
            backward(a,k);
        }

    }

法二：3次反转算法

确实很巧妙，这个有点类似于矩阵的逆矩阵的运算。
只需要编写反转的算法即可。
这里延用了我学习数据结构时数组就地逆址的算法。
下面给出所有代码：

public static void reverse(int a[],int i ,int j){
        for(int k=i;k<=(i+j)/2;k++)
        {
            int temp=a[k];
            a[k]=a[i+j-k];
            a[i+j-k]=temp;
        }
    }
    public static void exchange(int a[],int k){
        reverse(a,0,k);
        reverse(a,k+1,a.length-1);
        reverse(a,0,a.length-1);
//        reverse(a,0,a.length-1);
//        reverse(a,0,a.length-2-k);
//        reverse(a,a.length-k-1,a.length-1);

    }

大家可能好奇exchange中注释掉的代码是什么含义，这是我由这个算法受到启发，想出的调换反转的顺序一样可以解决。先反转原数组，这里要注意了，分割位点已经到了对称的位置，再分别反转位点左右两侧的子数组，完成换位！
如图：

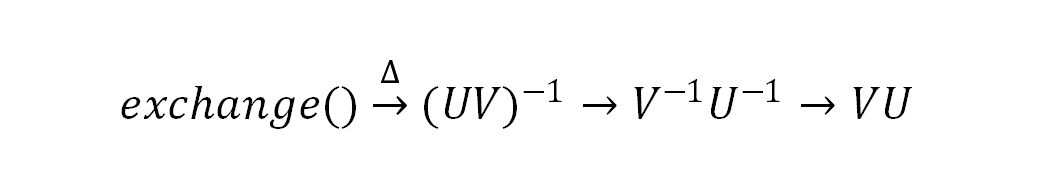
法二：排列循环算法

这个算法应该是跟离散数学中的循环置换子群有关，不过当时没有讲。这个算法确实很难懂。还涉及到了欧几里得法gcd(x,y)求最大公因数。

public static int gcd(int x,int y){
        if(x<y){
            int temp=x;
            x=y;
            y=temp;
        }
        while (x%y!=0){
            int r=x%y;
            x=y;
            y=r;

        }
        return y;
    }

不过答案给的方法有点问题，以{1,2,3,4,5,6,7,8}为例，当k=5时，此处分割位置应该是6的位置（下标为5），可是答案运行出来分割位置是5的位置，针对这个问题我做了修改可以解决这一小问题。

 public static void exchange(int a[],int k,int n)
 {
        int cyc=gcd(k+1,n-k-1);
        for (int i = 0;i <cyc; i++) 
        {
            int t=a[i];
            int p=i,j=(k+i+1)%n;
            while (i!=j)
            {
                a[p]=a[j];
                p=j;
                j=(k+1+p)%n;
            }
            a[p]=t;

        }
    }

好了，本次算法就分析到这里，这道题目算是做透了，不过如果要求用递归分治算法的请看我上一篇博客递归分治算法
有什么问题，欢迎评论留言！，谢谢大家！！