15445 lecture#4 Database Storage 2

1 Data Representation

A data representation scheme is how a DBMS stores the bytes for a value. There are five high level datatypes that can be stored in tuples: integers, variable-precision numbers, fixedpoint precision numbers, variable length values, and dates/times.

DBMS对于某个类型的值，存成什么样的字节（就是编码的意思吧）

Integers

Most DBMSs store integers using their “native” C/C++ types as specified by the IEEE-754 standard. These values are fixed length. Examples: INTEGER, BIGINT, SMALLINT, TINYINT.

↑上面notes错了啊，754是浮点数。应该只有黑体是对的

Variable-Length Data

有一个header，保存string的长度，以便快速调到下一个值。也包含一个checksum

Most DBMSs do not allow a tuple to exceed the size of a single page. The ones that do store the data on a special “overflow” page and have the tuple contain a reference to that page. These overflow pages can contain pointers to additional overflow pages until all the data can be stored.

这里提到了一个overflow page，注意和书里看到的overflow block不一样，那个是指找不到freespace之后放置新record的地方，这里指的是存放大文件的page

overflow page在存放数据之前，可以存放指向其他overflow page的指针（？？）

Some systems will let you store these large values in an external file, and then the tuple will contain a pointer to that file. For example, if the database is storing photo information, the DBMS can store the photos in the external files rather than having them take up large amounts of space in the DBMS. One downside of this is that the DBMS cannot manipulate the contents of this file. Thus, there are no durability or transaction protections.

这里和书里写的 一样，将large obj作为外部文件保存

Examples: VARCHAR, VARBINARY, TEXT, BLOB

Dates and Times

一般是保存为某个时间（unix epoch）之后的单位时间数

Examples: TIME, DATE, TIMESTAMP.

System Catalogs

DBMS为了理解tuple的内容，维护了一个internal catalog，记录DB的元数据，包含的信息:该DB里有什么表，哪些column，以及类型和ordering of value（？？）

大多数DBMS将他们的catalog保存在内部，使用的格式和他们用于存储表的格式相同（？？），使用特殊的代码来bootstrap他们的catalog table

这里说的类似mysql里的information_schema？

2 Workloads

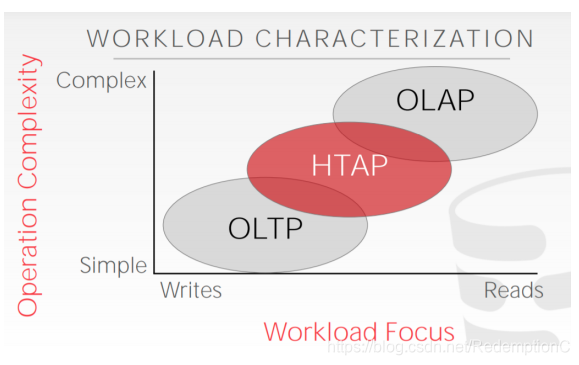
DBMS可能碰到的workload有许多种，主要分为：Online Transaction Processing和Online Analytical Processing

OLTP

特点是：fast，short running operation，简单的query，一次只查单个relation，很多重复的操作

一般是写多于读

An example of an OLTP workload is the Amazon storefront. Users can add things to their cart, they can make purchases, but the actions only affect their account.

OLAP

特点：long running，complex query，读很多的内容。通常是对OLTP产生的数据进行分析产生新数据

An example of an OLAP workload would be Amazon computing the five most bought items over a one month period for these geographical locations.

HTAP: Hybrid Transaction + Analytical Processing

3 Storage Models

在page中存储tuple的方式有很多种，到目前位置一直都是假设的n-ary storage model

N-Ary Storage Model (NSM)

这种方式下，DBMS将一个tuple的所有attr连续的放在一个page里，也被称为row store（行存储），这种适合于OLTP（存的多的，并且操作主要集中在一个entity。entity这里是指relation？）这种之所以理想是因为一次就能拿到一个tuple的全部attr

优点

快速插入，更新，删除；对于需要一整个tuple(比如select *)的很方便

缺点

如果需要扫描表的大部分，或者只需要attr的一个子集，则不太友好

因为buffer pool会取到不需要的数据（需要的不需要的混在一个block/page）

Decomposition Storage Model (DSM)

这种就是column store,将一个表中某个attr的所有值存在一起，这种适合于OLAP，因为查询操作更多，或者只需要attrs的一个子集

优点

查询时减少了无效工作，只读自己需要的attr

更方便压缩，因为同类型（同attr）的都存在一起了（怎么压缩？）

缺点

插入，更新，删除慢，点查询（应该就是指查某个tuple的全部属性？）因为一个tuple没有整个存在一起，可能这个attr在这，那个attr在那

当使用column store时，为了将一个tuple再拼起来，有两种常用方法：

The most commonly used approach is fixed-length offsets. Assuming the attributes are all fixed-length, the DBMS can compute the offset of the attribute for each tuple. Then when the system wants the attribute for a specific tuple, it knows how to jump to that spot in the file from the offest. To accommodate the variable-length fields, the system can either pad fields so that they are all the same length or use a dictionary that takes a fixed-size integer and maps the integer to the value

这里是指attr的长度固定，那么DBMS就能算出属于某个tuple的某个attr的offset（这需要知道在第几个吧？）

对于变长的attr，一种办法是对齐，以便让他们长度相等，或者使用dictionary，？？？没懂

A less common approach is to use embedded tuple ids. Here, for every attribute in the columns, the DBMS stores a tuple id (ex: a primary key) with it. The system then would also store a mapping to tell it how to jump to every attribute that has that id. Note that this method has a large storage overhead because it needs to store a tuple id for every attribute entry

一个不那么常用的方法：为每个attr维护一个所属tuple的id，另外DBMS再维护一个mapping，使得其能直接到有该id的attr

但这种做法开销很大，因为需要为每个attr值保存一个tuple id