算法就是任何良定义的计算过程,该过程取某个值或值的集合作为输入并产生某个值或值的集合作为输出。——《算法导论》
时间复杂度
什么是时间复杂度,先看一下百度描述
一般情况下,算法中基本操作重复执行的次数是问题规模 n n n 的某个函数,用 T ( n ) T(n) T(n) 表示,若有某个辅助函数 g ( n ) g(n) g(n),存在一个正常数 c c c 使得 c g ( n ) ⩾ T ( n ) cg(n) \geqslant T(n) cg(n)⩾T(n) 恒成立。记作 T ( n ) = O ( g ( n ) ) T(n)=O(g(n)) T(n)=O(g(n)),称 O ( g ( n ) ) O(g(n)) O(g(n)) 为算法的渐进时间复杂度,简称时间复杂度。
这段话什么意思?话不多说,以一个例子说明上面那段话的含义,先看一段伪代码(伪代码来源于《算法导论》)
INSERTION-SORT(A) 代价 执行次数
for j = 2 to A.length c1 n
key = A[j] c2 n-1
//Insert A[j] into the sorted A[1..j-1] 0 n-1
i = j - 1 c4 n-1
while i>0 and A[i]>key c5 N
A[i+1] = A[i] c6 N2
i = i - 1 c7 N2
A[i+1] = key c8 n-1
(上面代码中N的含义为
N
=
∑
j
=
2
n
t
j
N=\sum_{j=2}^nt_j
N=∑j=2ntj,N2的含义为
N
2
=
∑
j
=
2
n
(
t
j
−
1
)
N2=\sum_{j=2}^n{(t_j-1)}
N2=∑j=2n(tj−1),
t
j
t_j
tj指第
j
j
j 次循环时while执行的次数)
上面是插入排序的伪代码,并且在每一行标记了代码的执行代价和执行次数,假设输入具有n个值,下面计算它的运行时间
T
(
n
)
=
c
1
n
+
c
2
(
n
−
1
)
+
c
4
(
n
−
1
)
+
c
5
∑
j
=
2
n
t
j
+
c
6
∑
j
=
2
n
(
t
j
−
1
)
+
c
7
∑
j
=
2
n
(
t
j
−
1
)
+
c
8
(
n
−
1
)
T(n) = c_1n+c_2(n-1)+c_4(n-1)+c_5\sum_{j=2}^nt_j + c_6\sum_{j=2}^n{(t_j-1)} + c_7\sum_{j=2}^n{(t_j-1)} + c_8(n-1)
T(n)=c1n+c2(n−1)+c4(n−1)+c5j=2∑ntj+c6j=2∑n(tj−1)+c7j=2∑n(tj−1)+c8(n−1)
t
j
t_j
tj的具体值由输入的情况决定,如果输入数组已递减排序,将导致插入排序进入最坏情况,此时
t
j
=
j
t_j=j
tj=j,则N和N2分别等于
N
=
∑
i
=
2
n
t
j
=
∑
i
=
2
n
j
=
n
(
n
+
1
)
2
−
1
N
2
=
∑
i
=
2
n
(
t
j
−
1
)
=
∑
i
=
2
n
(
j
−
1
)
=
n
(
n
−
1
)
2
N=\sum_{i=2}^nt_j=\sum_{i=2}^nj=\frac{n(n+1)}2-1\\ N2=\sum_{i=2}^n{(t_j-1)}=\sum_{i=2}^n{(j-1)}=\frac{n(n-1)}2
N=i=2∑ntj=i=2∑nj=2n(n+1)−1N2=i=2∑n(tj−1)=i=2∑n(j−1)=2n(n−1)
此时
T
(
n
)
等
于
T(n)等于
T(n)等于
T
(
n
)
=
(
c
5
2
+
c
6
2
+
c
7
2
)
n
2
+
(
c
1
+
c
2
+
c
4
+
c
5
2
−
c
6
2
−
c
7
2
+
c
8
)
n
+
(
−
c
2
−
c
4
−
c
5
−
c
8
)
T(n)=(\frac{c_5}2+\frac{c_6}2+\frac{c_7}2)n^2+(c_1+c_2+c_4+\frac{c_5}2-\frac{c_6}2-\frac{c_7}2 + c_8)n+(-c_2-c_4-c_5-c_8)
T(n)=(2c5+2c6+2c7)n2+(c1+c2+c4+2c5−2c6−2c7+c8)n+(−c2−c4−c5−c8)
这是一个关于
n
n
n 的二次函数,可以简写为:
a
n
2
+
b
n
+
c
an^2+bn+c
an2+bn+c。当
n
n
n 很大时,常数项和低阶项相对来说不太重要,所以忽略低阶项和常数项。同时,我们也忽略最高阶项的常系数,因为对于较大的输入,在确定计算效率时常量因子不如增长率重要。现在式子里只剩下
n
2
n^2
n2,不妨令
g
(
n
)
=
n
2
g(n)=n^2
g(n)=n2。不难发现
T
(
n
)
T(n)
T(n)与
g
(
n
)
g(n)
g(n)有如下关系:
- 存在一个正的常量 c c c,使得 T ( n ) ⩽ c g ( n ) T(n) \leqslant cg(n) T(n)⩽cg(n) 对于一个足够大的 n n n 恒成立,此时记 T ( n ) = O ( g ( n ) ) T(n)=O(g(n)) T(n)=O(g(n)) 也就是 T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
- 存在一个正的常量 c c c,使得 T ( n ) ⩾ c g ( n ) T(n) \geqslant cg(n) T(n)⩾cg(n) 对于一个足够大的 n n n 恒成立,此时记 T ( n ) = Ω ( g ( n ) ) T(n)= \Omega(g(n)) T(n)=Ω(g(n)) 也就是 T ( n ) = Ω ( n 2 ) T(n)= \Omega(n^2) T(n)=Ω(n2)
- 综合1和2,有存在两个正的常量 c 1 c_1 c1和 c 2 c_2 c2,使得 c 1 g ( n ) ⩽ T ( n ) ⩽ c 2 g ( n ) c_1g(n)\leqslant T(n) \leqslant c_2g(n) c1g(n)⩽T(n)⩽c2g(n) 对于一个足够大的 n n n 恒成立,此时记 T ( n ) = Θ ( g ( n ) ) T(n)= \Theta(g(n)) T(n)=Θ(g(n)) 也就是 T ( n ) = Θ ( n 2 ) T(n)= \Theta(n^2) T(n)=Θ(n2)。
(以上关系可以通过数学推导证明,在此不再给出,有兴趣的同学可以参考《算法导论》第三章。)
上面的 O O O、 Ω \Omega Ω 和 Θ \Theta Θ 可以在一定程度上替代T(n)衡量算法的运行时间代价,我们将这些符号称之为渐近记号。
渐近记号
渐近记号用来刻画算法的运行时间,也就是我们通常说的时间复杂度。在《算法导论》中,一共介绍了5种渐进记号,如下表所示
| 记号 | 含义 | 相对增长率 |
|---|---|---|
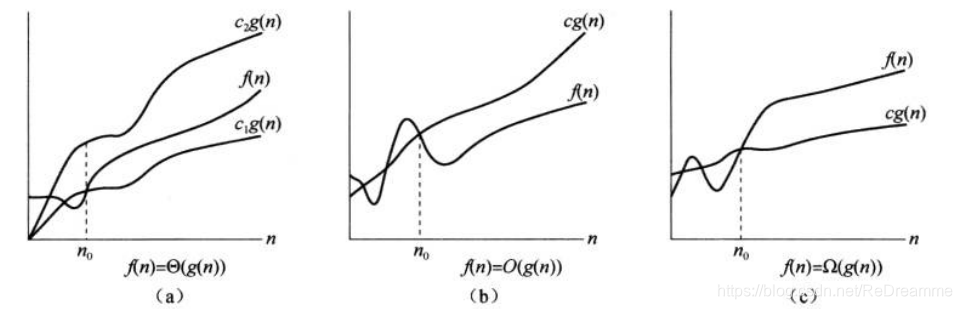
| f ( n ) = Θ ( g ( n ) ) f(n) = \Theta(g(n)) f(n)=Θ(g(n)) | 对于 f(n) 存在正常量 c 1 c_1 c1、 c 2 c_2 c2和 n 0 n_0 n0使得对所有 n ⩾ n 0 n\geqslant n_0 n⩾n0,有 0 ⩽ c 1 g ( n ) ⩽ f ( n ) ⩽ c 2 g ( n ) 0\leqslant c_1g(n)\leqslant f(n) \leqslant c_2g(n) 0⩽c1g(n)⩽f(n)⩽c2g(n) | f(n) 的增长率$ =$ g(n)的增长率 |
| f ( n ) = O ( g ( n ) ) f(n) = O(g(n)) f(n)=O(g(n)) | 对于 f(n) 存在正常量 c c c和 n 0 n_0 n0使得对所有 n ⩾ n 0 n\geqslant n_0 n⩾n0,有 0 ⩽ f ( n ) ⩽ c g ( n ) 0\leqslant f(n) \leqslant cg(n) 0⩽f(n)⩽cg(n) | f(n) 的增长率 ⩽ \leqslant ⩽ g(n)的增长率 |
| f ( n ) = Ω ( g ( n ) ) f(n) = \Omega(g(n)) f(n)=Ω(g(n)) | 对于 f(n) 存在正常量 c c c和 n 0 n_0 n0使得对所有 n ⩾ n 0 n\geqslant n_0 n⩾n0,有 0 ⩽ c g ( n ) ⩽ f ( n ) 0\leqslant cg(n)\leqslant f(n) 0⩽cg(n)⩽f(n) | f(n) 的增长率 ⩾ \geqslant ⩾ g(n)的增长率 |
| f ( n ) = o ( g ( n ) ) f(n) = o(g(n)) f(n)=o(g(n)) | 对于 f(n) 存在正常量 c > 0 c>0 c>0和 n 0 > 0 n_0>0 n0>0 使得对所有 n ⩾ n 0 n\geqslant n_0 n⩾n0,有 0 ⩽ f ( n ) < c g ( n ) 0\leqslant f(n)<cg(n) 0⩽f(n)<cg(n) | f(n) 的增长率 > > > g(n)的增长率 |
| f ( n ) = ω ( g ( n ) ) f(n) = \omega(g(n)) f(n)=ω(g(n)) | 对于 f(n) 存在正常量 c > 0 c>0 c>0和 n 0 > 0 n_0>0 n0>0使得对所有 n ⩾ n 0 n\geqslant n_0 n⩾n0,有 0 ⩽ c g ( n ) < f ( n ) 0\leqslant cg(n)< f(n) 0⩽cg(n)<f(n) | f(n) 的增长率 < < < g(n)的增长率 |
上表中的前三中记号在上一小节已经提到过,他们之间有如下关系:
定理 1
Θ
(
g
(
n
)
)
=
O
(
g
(
n
)
)
∩
Ω
(
g
(
n
)
)
\Theta(g(n)) = O(g(n))\cap\Omega(g(n))
Θ(g(n))=O(g(n))∩Ω(g(n))
到此渐近记号的基本概念已经介绍完毕,出于完整性考虑,下面简要提一下其他细节性的概念,详情仍然可以参考《算法导论》第三章。
更多解释(可略过)
Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))记号: f ( n ) = Θ ( g ( n ) ) f(n) = \Theta(g(n)) f(n)=Θ(g(n)) 表示函数 f ( n ) f(n) f(n)在一个常数因子内等于 g ( n ) g(n) g(n),此时称 g ( n ) g(n) g(n)是 f ( n ) f(n) f(n)的一个渐进紧确界(asymptotically tight bound)。 Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))的定义要求每个成员 f ( n ) ∈ ( g ( n ) ) f(n)\in(g(n)) f(n)∈(g(n))均渐进非负,即当n足够大时,f(n)非负,所以 g ( n ) g(n) g(n)本身必须非负,否则 Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))为空。
O ( g ( n ) ) O(g(n)) O(g(n))记号: Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))记号给出了一个函数的上界和下界。当只有一个渐进上界时,使用 O O O记号,它给出了函数的一个在常量因子内的上界。
O m e g a ( g ( n ) ) Omega(g(n)) Omega(g(n))记号:类似地当只有一个渐进下界时,使用 Ω \Omega Ω 记号,它给出了函数的一个在常量因子内的下界。
f ( n ) = Θ ( g ( n ) ) f(n) = \Theta(g(n)) f(n)=Θ(g(n))蕴含着 f ( n ) = O ( g ( n ) ) f(n) = O(g(n)) f(n)=O(g(n))和 f ( n ) = Ω ( g ( n ) ) f(n) = \Omega(g(n)) f(n)=Ω(g(n)) ,它是一个更强的概念,按照集合论的写法,有: Θ ( g ( n ) ) ⊂ O ( g ( n ) ) \Theta(g(n))\subset O(g(n)) Θ(g(n))⊂O(g(n))、 Θ ( g ( n ) ) ⊂ Ω ( g ( n ) ) \Theta(g(n))\subset \Omega(g(n)) Θ(g(n))⊂Ω(g(n))。它们的图像如下所示
o ( g ( n ) ) o(g(n)) o(g(n))记号:O记号提供的上界可能是也可能不是紧确的,例如 2 n = O ( n 2 ) 2n = O(n^2) 2n=O(n2),这个等式是正确的但不是紧确的,紧确的形式应当是 2 n = O ( n ) 2n = O(n) 2n=O(n)。可以使用 o o o记号表示一个非渐进紧确的上界。
ω ( g ( n ) ) \omega(g(n)) ω(g(n))记号:与 o o o记号类似, ω ( g ( n ) ) \omega(g(n)) ω(g(n))记号用来提供非渐进紧确的下界
这5类符号有很多性质,例如传递性、自反性和对称性等,这里不再介绍。
Tips:渐近记号可以用来刻画算法的运行时间,但也能描述算法的其他方面。即使使用渐进记号刻画算法的运行时间,也要注意指的是哪种情况的运行时间(最好、最坏、平均)。
更多举例
再多的理论也不如几个例子简单明了,下面举两个例子
f ( n ) = n + 1 f(n)=n+1 f(n)=n+1
令 c = 2 , g ( n ) = n c=2,g(n)=n c=2,g(n)=n,当 n ⩾ 1 n\geqslant 1 n⩾1时,有 f ( n ) ⩽ c g ( n ) f(n)\leqslant cg(n) f(n)⩽cg(n)
所以有 f ( n ) = O ( g ( n ) ) = O ( n ) f(n)=O(g(n))=O(n) f(n)=O(g(n))=O(n)
注意:我们也可以选 c = 1 , g ( n ) = n 2 c=1,g(n) = n^2 c=1,g(n)=n2 ,仍然有当 n ⩾ 2 n\geqslant 2 n⩾2时 f ( n ) ⩽ c g ( n ) f(n)\leqslant cg(n) f(n)⩽cg(n)。但此时O记号提供的上界不是紧确的(可以说 f ( n ) = o ( n 2 ) f(n)=o(n^2) f(n)=o(n2)),所以选择 g ( n ) = 2 n g(n)=2n g(n)=2n更加精确
f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n
令 c = 2 , g ( n ) = n 2 c=2,g(n)=n^2 c=2,g(n)=n2,当 n ⩾ 1 n\geqslant 1 n⩾1时,有 f ( n ) ⩽ c g ( n ) f(n)\leqslant cg(n) f(n)⩽cg(n)
所以有 f ( n ) = O ( g ( n 2 ) ) = O ( n 2 ) f(n)=O(g(n^2))=O(n^2) f(n)=O(g(n2))=O(n2)
令 c = 1 , g ( n ) = n 2 c=1,g(n)=n^2 c=1,g(n)=n2,当 n ⩾ 1 n\geqslant 1 n⩾1时,有 c g ( n ) ⩽ f ( n ) cg(n)\leqslant f(n) cg(n)⩽f(n)
所以有 f ( n ) = Ω ( g ( n 2 ) ) = Ω ( n 2 ) f(n)=\Omega(g(n^2))=\Omega(n^2) f(n)=Ω(g(n2))=Ω(n2)
综上,由定理 1可得到 f ( n ) = Θ ( g ( n 2 ) ) f(n)=\Theta(g(n^2)) f(n)=Θ(g(n2))





 本文深入解析算法的时间复杂度概念,通过具体实例详细阐述了O、Ω和Θ等渐近记号的含义及应用,帮助读者理解算法效率评估的关键方法。
本文深入解析算法的时间复杂度概念,通过具体实例详细阐述了O、Ω和Θ等渐近记号的含义及应用,帮助读者理解算法效率评估的关键方法。
















 1853
1853

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








