【字符串】KMP算法

对于正常的字符串模式匹配，主串长度为m，子串为n，时间复杂度会到达O（m*n），而如果用KMP算法，复杂度将会减少线型时间O（m+n）。

KMP这个是查找这个串在母串的位置
洛谷P3375

#include<bits/stdc++.h>
using namespace std;

char s[1000005],p[1000005];
int net[1000005];
void getnext(char *p){
    int lenp=strlen(p);
    net[0]=-1;
    int k=-1;
    int j=0;
    while(j<lenp){
        if(k==-1||p[j]==p[k]){
            j++;k++;
            net[j]=k;
        }
        else
            k=net[k];
    }
}

vector<int> vec;
void kmp(char *s,char *p){
    int lens=strlen(s);
    int lenp=strlen(p);
    int i=0,j=0;
    while(i<lens){
        if(j==-1||s[i]==p[j]){
            i++;j++;
        }
        else j=net[j];
        if(j==lenp){
			vec.push_back(i-lenp+1);
           	j=net[j];
		}
    }
}

int main(){
	scanf("%s",s);	
	scanf("%s",p);	
    getnext(p);
	kmp(s,p);
	for(auto it:vec) cout<<it<<endl;
	for(int i=1;i<=strlen(p);i++){
		cout<<net[i]<<" ";
	}
	puts("");
    return 0;
}

如果觉得KMP难以理解没关系，我们可以用C++STL的find函数替代！

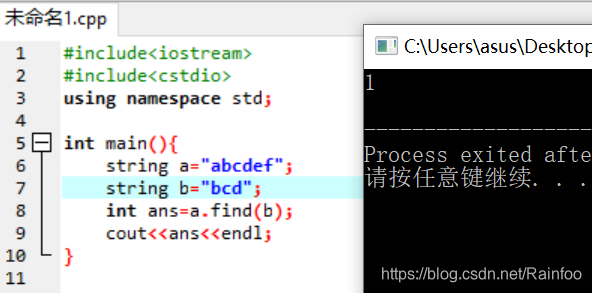
不过这个时间复杂度是O(m*n），大于KMP算法