求解同余方程数论扩展欧几里得

原创已于 2022-08-01 10:38:54 修改 · 164 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2022-07-31 22:42:46 首次发布

码题集专栏收录该内容

12 篇文章

订阅专栏

本文介绍了扩展欧几里得算法及其在解决不定方程a⋅x+b⋅y=1中的应用，同时阐述了裴蜀定理，说明了如何找到该方程的一组解及所有解的通式。通过示例代码展示了如何利用扩展欧几里得算法求解整数解，并给出了一种边界情况和一般情况的解法。

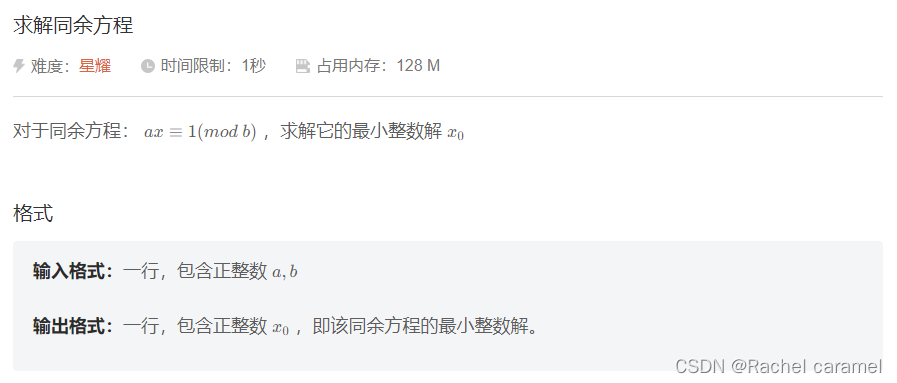
题面：
在这里插入图片描述

思路：
$a\cdot x=b\cdot y +1\\ a\cdot x-b\cdot y =1\\ \text{因为y的取值是任意的，因此可以将这个式子看成：}\\ a\cdot x+b\cdot y =1\\ \text{因为题目保证有解，所以a和b是互质的，即}\gcd(a,b)=1\\ \text{而扩展欧几里得就是用来求形如：} a\cdot x+b\cdot=c\text {的不定方程的整数解的}\\ \text{这里需要再补充一个裴蜀定理：}\\ \text{若}a,b\text{为整数，那么一定存在}a\cdot x+b\cdot y=\gcd(a,b)\\ \text{即}a\cdot x+b\cdot y \text{的值一定是}\gcd(a,b)\text{的倍数}\\ \text{先考虑边界情况}a\cdot 1+b\cdot 0=\gcd(a,b),\text{此时，}x=1,y=0\\ \text{然后考虑一般情况，假设某一次得到的解是}x_0、y_0\\ b\cdot x_0+(a\bmod b)\cdot y_0=\gcd(a,b)\\ b\cdot x_0+(a-\lfloor \frac a b \rfloor\cdot b)\cdot y_0=\gcd(a,b)\\ a\cdot y_0+b\cdot (x_0-\lfloor \frac a b \rfloor\cdot y_0)=\gcd(a,b)\\ \text{由此可得：} x=y_0 ,y=x_0-\lfloor \frac a b \rfloor\cdot y_0\\ \text{已知任意一组解}x_0,y_0\text{通解为：} \\ x=x0+ \frac{b} {\gcd (a,b)}\cdot n\\ x=x0+ \frac{b} {\gcd (a,b)}\cdot n\\$
代码：

#include <bits/stdc++.h>
#include <iostream>
using namespace std;
const int maxn=111111;
int a,b,x,y;

void exgcd(int a,int b,int *x,int *y)//扩展欧几里得算法
{
    //cout<<"a="<<a<<" "<<"b="<<b<<" "<<"x="<<*x<<" "<<"y="<<*y<<endl;
    if(b==0)
    {
        *x=1,*y=0;
        return;
    }
    exgcd(b,a%b,x,y); //r=GCD(a,b)=GCD(b, a%b)
    //cout<<"!!!a="<<a<<" "<<"b="<<b<<" "<<"x="<<*x<<" "<<"y="<<*y<<endl;
    int t=*x;
    *x=*y;
    *y=t-a/b*(*y) ;
    
}

int main()
{
    cin>>a>>b;
    exgcd(a,b,&x,&y);
    //cout<<"x="<<x<<" "<<"b="<<b<<endl;
    while(x<0) x+=b;
    cout<<x<<endl;
	return 0;
}