饥饿游戏搜索算法-HGS(函数优化/工程设计)

原创于 2025-01-28 10:47:27 发布 · 1.3k 阅读

CC 4.0 BY-SA版权

文章标签：

在算法研究的广袤领域中，饥饿游戏搜索算法（Hunger Games Search，HGS）作为一种基于群体智能的创新优化算法，独树一帜。它巧妙地从著名的饥饿游戏所蕴含的竞争与协作机制中汲取灵感，将现实世界中激烈的生存竞争场景抽象化，融入到算法的设计理念里，致力于在复杂的问题空间中，逐步探寻出最优质的解决方案。

核心思想

HGS 的核心，在于对个体在资源极度有限环境下行为的精妙模拟。它把整个求解过程视为一场激烈的生存角逐，个体间通过持续的竞争与协作，向着最优解不断迈进。在这一算法体系里，每一个个体都象征着一个潜在的解，而适应度函数则如同精准的 “价值天平”，能够公正地衡量出每个潜在解的优劣程度。个体依据适应度函数给出的评估结果，灵活地调整自身在解空间中的位置，就像在现实中，生物会根据环境的反馈来改变自身的生存策略一样。

主要步骤

初始化：在算法启动之初，会随机生成一组初始种群。这些种群中的每一个个体，都犹如在黑暗中摸索前行的探索者，代表着一个潜在的问题解决方案，它们被随机播撒在解空间的各个角落，为后续的搜索过程奠定基础。
适应度评估：针对生成的每一个个体，算法会迅速调用适应度函数，精准计算出其适应度值。这个数值直观地反映出个体所代表的潜在解在当前问题情境下的优劣状况，数值越高，意味着该解越接近理想状态，反之则离目标还有一定距离。
竞争与协作：在这一关键环节，个体之间展开了激烈的互动。竞争机制如同一场残酷的资源争夺战，每个个体都凭借自身的适应度值来争取更多的资源，适应度值越高，获取资源的能力就越强；协作则像是团队合作，个体之间通过信息共享，彼此交流在搜索过程中的发现和经验，以此来提高整个群体在解空间中的搜索效率，避免陷入局部最优的困境。
更新位置：基于竞争与协作的结果，个体开始调整自身在解空间中的位置。它们参考其他优秀个体的经验和自身的竞争优势，向着更有可能存在最优解的区域进发，不断优化自己所代表的潜在解。
迭代：算法会持续重复适应度评估、竞争与协作、位置更新这一系列步骤，如同永不停歇的探索引擎，直到满足预设的终止条件。这一过程中，每一次迭代都使算法更加接近最优解，逐步收敛到问题的最佳答案。

算法特点

自适应性：HGS 中的个体具备强大的自适应能力，它们能够像敏锐的环境观察者一样，实时感知周围环境的变化，并依据这些动态信息灵活调整自身的搜索策略。无论是面对复杂多变的问题空间，还是在搜索过程中遇到的各种干扰因素，个体都能迅速做出反应，确保搜索过程的高效性和准确性。
全局与局部搜索平衡：通过独特的竞争与协作机制，HGS 在全局探索和局部开发之间找到了完美的平衡点。在搜索初期，个体通过广泛的竞争和信息共享，积极探索解空间的各个角落，尽可能地发现潜在的优质区域；随着搜索的深入，个体之间的协作逐渐加强，它们聚焦于已经发现的优质区域，进行细致的局部开发，深入挖掘其中的最优解，从而实现了在不同搜索阶段的高效运作。
鲁棒性：在处理复杂、多峰优化问题时，HGS 展现出了卓越的鲁棒性。它能够有效应对问题空间中存在的多个局部最优解，避免算法陷入局部陷阱，始终保持对全局最优解的搜索能力。无论是面对何种复杂的函数形式，还是在高维度、多约束的问题环境下，HGS 都能凭借其独特的算法设计，稳定地输出高质量的解决方案。

应用领域

凭借其高效的搜索能力和出色的适应性，HGS 在众多领域都展现出了巨大的应用潜力。在函数优化领域，它能够快速准确地找到复杂函数的最优解，为数学建模和科学计算提供有力支持；在工程设计中，HGS 可以帮助工程师在众多设计参数中寻找到最佳组合，优化产品性能，降低成本；在机器学习参数调优方面，HGS 能够自动搜索出最优的参数配置，提高模型的准确性和泛化能力，助力机器学习算法在各个领域的高效应用。

具体代码及实验结果

%%
clc
clear
close all
%%

%%
Fun_name = 'F7'; % 测试函数名称: 'F1' 到 'F23'

SearchAgents = 30;               % 搜索代理数量（种群成员）
Max_iterations = 1000;           % 最大迭代次数
[lowerbound, upperbound, dimension, fitness] = fun_info(Fun_name); % 获取目标函数信息
[Best_score, Best_HGSs, HGS_curve] = HGS(SearchAgents, Max_iterations, lowerbound, upperbound, dimension, fitness); % 使用HGS求解问题
%%

% 显示结果
display(['The best solution obtained by HGS for ', Fun_name, ' is: ', num2str(Best_HGSs)]);
display(['The best optimal value of the objective function found by HGS for ', Fun_name, ' is: ', num2str(Best_score)]);

% 绘图
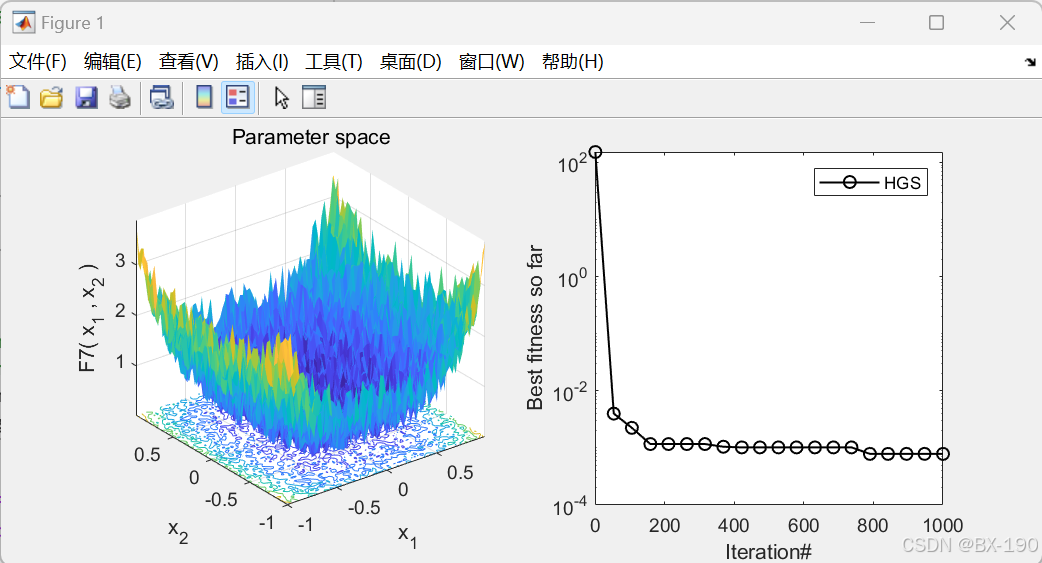
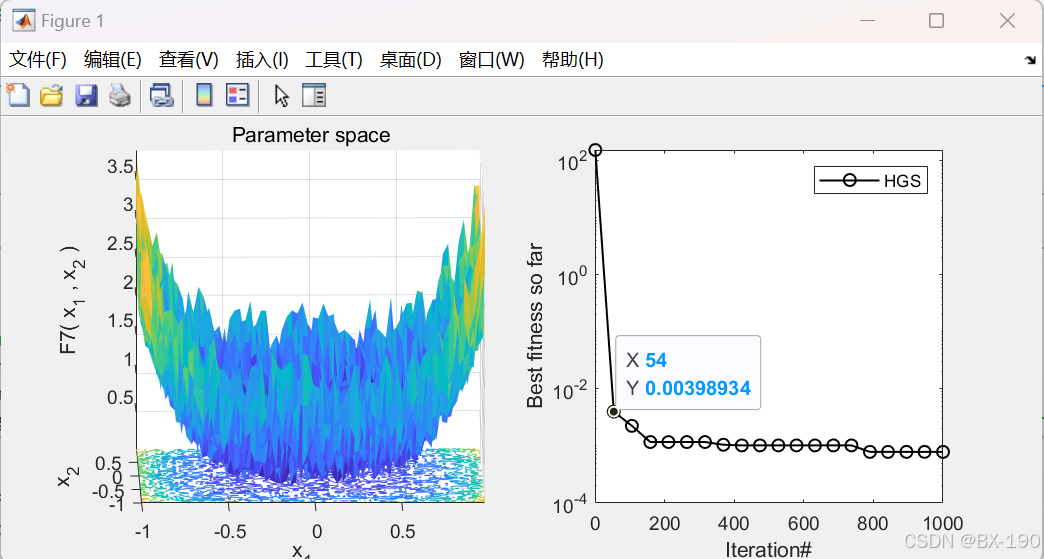
figure('Position', [454, 445, 694, 297]);
subplot(1, 2, 1);
func_plot(Fun_name); % 绘制函数图像
title('Parameter space');
xlabel('x_1');
ylabel('x_2');
zlabel([Fun_name, '(x_1, x_2)']);

subplot(1, 2, 2); % 绘制收敛曲线
CNT = 20; % 选择20个点绘制
k = round(linspace(1, Max_iterations, CNT)); % 在迭代范围内均匀选择点

if ~strcmp(Fun_name, 'F16') && ~strcmp(Fun_name, 'F9') && ~strcmp(Fun_name, 'F11') % 排除某些函数
    semilogy(k, HGS_curve(k), 'k-o', 'LineWidth', 1); % 使用半对数图
else
    plot(k, HGS_curve(k), 'k-o', 'LineWidth', 1); % 使用普通图
end

xlabel('Iteration#');
ylabel('Best fitness so far');
legend('HGS');