dp算法篇Day9

"抱紧你的我，比国王富有" 

---

 

41、最长公共子序列

(1) 题目解析

        同之前子序列问题不同的是，这次题目要求是分别从两个不同的字符串中，查找相同的子序串。 

(2) 算法原理

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size();
        int n = text2.size();
        text1 = " " + text1,text2 = " " + text2;

        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=1;i<=m;++i)
        {
            for(int j=1;j<=n;++j)
            {
                if(text1[i] == text2[j]) dp[i][j] = dp[i-1][j-1]+1;
                else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        } 
        return dp[m][n];
    }
};

 

---

42、不相交的线

(1) 题目解析

        当多画几个测试用例时，你就会发现，这似乎就是从上下两个数组中，选取相同的数，因为题目的要求是"不相交"的线，也就保证了选取的数在原数组中的顺序是相对确定的，本质上就是选取子序列数组！

(2) 算法原理

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();

        vector<vector<int>> dp(m+1,vector<int>(n+1));

        for(int i=1;i<=m;++i)
        {
            for(int j=1;j<=n;++j)
            {
                if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1]+1;
                else dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
            }
        }
        
        return dp[m][n];
    }
};

---

43、不同的子序列

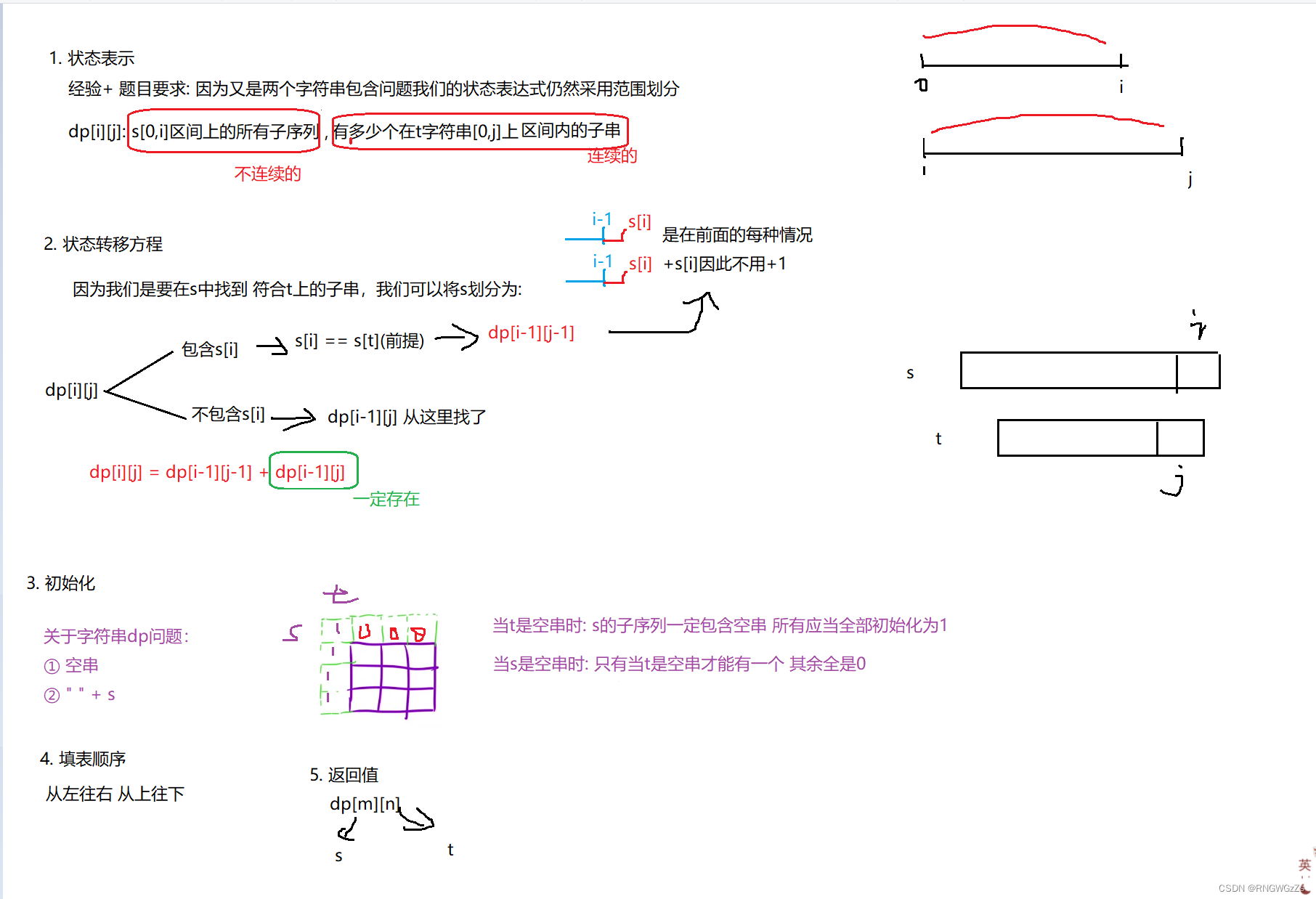
(1) 题目解析

 

(2) 算法原理

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.size();
        int n = t.size();

        vector<vector<double>> dp(m+1,vector<double>(n+1));
        // 当t为空串 初始化s为1
        for(int i=0;i<=m;++i) dp[i][0] = 1;

        for(int i=1;i<=m;++i)
        {
            for(int j=1;j<=n;++j)
            {
                if(s[i-1] == t[j-1]) dp[i][j] += dp[i-1][j-1];
                // 这里可能存在溢出
                dp[i][j] += dp[i-1][j];
            }   
        }

        return dp[m][n];
    }
};

        

---

44、通配符匹配

(1) 题目解析

 

(2) 算法原理

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();

        s = " " + s,p = " " + p;
        vector<vector<bool>> dp(m+1,vector<bool>(n+1));
        // 初始化第一行:
        dp[0][0] = true;
        for(int j=1;j<=n;++j)
            if(p[j] == '*') dp[0][j] = true;
            else break;

        for(int i=1;i<=m;++i)
        {
            for(int j=1;j<=n;++j)
            {
                if(p[j] == '*') dp[i][j] = dp[i-1][j] || dp[i][j-1];
                else dp[i][j] = (p[j] == '?' || s[i] == p[j]) && (dp[i-1][j-1]);
            }
        }
        return dp[m][n];
    }
};

 

---

45、正则表达式匹配

(1) 题目解析

         注意，这个题目的"*"通配符，在它之前一定需要存在一个有效的字符！才能使用。

(2) 算法原理

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();

        s = " " + s,p = " " + p;
        vector<vector<bool>> dp(m+1,vector<bool>(n+1));
        dp[0][0] = true;
        for(int j=2;j<=n;j+=2)
        {
            // 偶数位置 
            if(p[j] == '*') dp[0][j] = true;
            else break;
        }
    
        for(int i=1;i<=m;++i)
        { 
            for(int j=1;j<=n;++j)
            {
                if(p[j] == '*') 
                    dp[i][j] = dp[i][j-2] || ( (p[j-1] == '.' || p[j-1] == s[i]) && dp[i-1][j] );
                else 
                    dp[i][j] = (p[j] == '.' || p[j] == s[i]) && dp[i-1][j-1];
            }
        }

        return dp[m][n];
    } 
};

---

本篇到此结束，感谢你的阅读。

祝你好运，向阳而生~