二叉树与树的概念

从前有棵树，上面挂了很多学生，叫做“高数”。又走着走着，看见一颗树，上面挂着学生，

叫做“二叉树” ……

-------前言

---

(1)树的概念以及结构:

①数的结构:

树，和之前说的链表、顺序表一样，都是一种数据结构。

但：树是一种 非线性的数据结构， 它是由 n （ n>=0 ）个有限结点组成一个 具有层次关系的集合 。

把它 叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。

②树的结构:

任何树都是有一个"根节点"和其他"子节点"构成。

根节点:是一个特殊的节点( 根节点没有前驱结点)。

 叶节点:没有"后继"的节点。

每棵子树的根结点有且只有一个前驱，可以 有0个或多个后继

子树不相交

 图示:G有多个前驱节点，因此不是树。

(2)树的相关术语:

①节点的度：一个节点含有的子树的个数称为该节点的度

如:A的度为6 、E的度为2

②树的度:一棵树中，最大的节点的度称为树的度

如:树的度为6

③叶节点或终端节点：度为0的节点称为叶节点(没有子节点的树)

如:B、C、H、I。

④非终端节点或分支节点：：度不为0的节点

如:D、E、F、G。

⑤节点的层次:从根开始定义起，根为第1层，根的子节点为第2层。

⑥树的高度或深度:树中节点的最大层次

如:树的高度为4。

 以上就是树相关的内容铺垫啦~。

(一)二叉树的结构和概念

概念:

一棵二叉树是结点的一个有限集合，该集合或者为空，

或者是由一个根节点加上两棵别称为 左子树 和 右子树 的二叉树组成。

特点:

1. 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。

2. 二叉树的子树有左右之分，其子树的次序不能颠倒。

 结构：

特殊二叉树:

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

满二叉树:

 完全二叉树:

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。

对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号。

从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

(二)二叉树的存储结构和性质:

存储结构:

二叉树一般可以使用两种结构存储，一种 顺序结构 ，一种 链式结构 。

二叉树性质:

1. 若规定 根节点的层数为1 ，则 一棵非空二叉树的第i层上最多有2^(i-1) 个结点

2. 若规定 根节点的层数为1 ，则 深度为h 的 二叉树的最大结点数是2^h- 1 .

3. 对任何一棵二叉树 , 如果度为 0 其叶结点个数为 n0, 度为 2 的分支结点个数为 n2, 则有 n0 ＝ n2

＋ 1

4. 4. 若规定 根节点的层数为1 ，具有 n个结点的满二叉树的深度，h=LogN .

(三)二叉树的实现:

二叉树三序:

前序:根 左子树 右子树

中序:左子树 根 右子树

后序:左子树 右子树 根

①二叉树的变量创建: 

②创建节点

并链接:
 

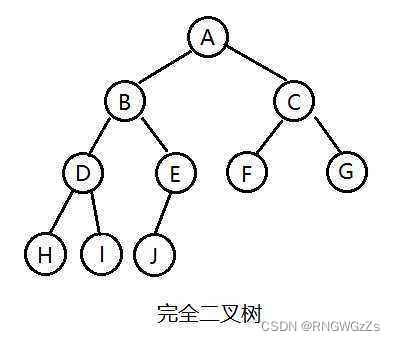
③ 前序：根、左子树、右子树

---

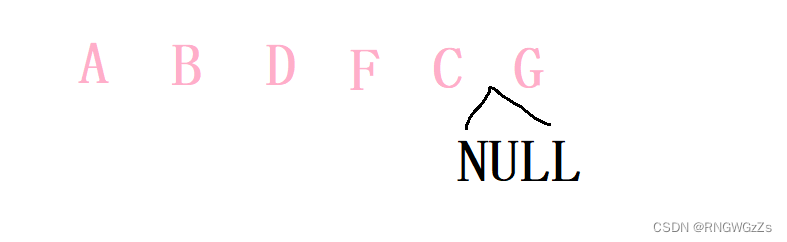
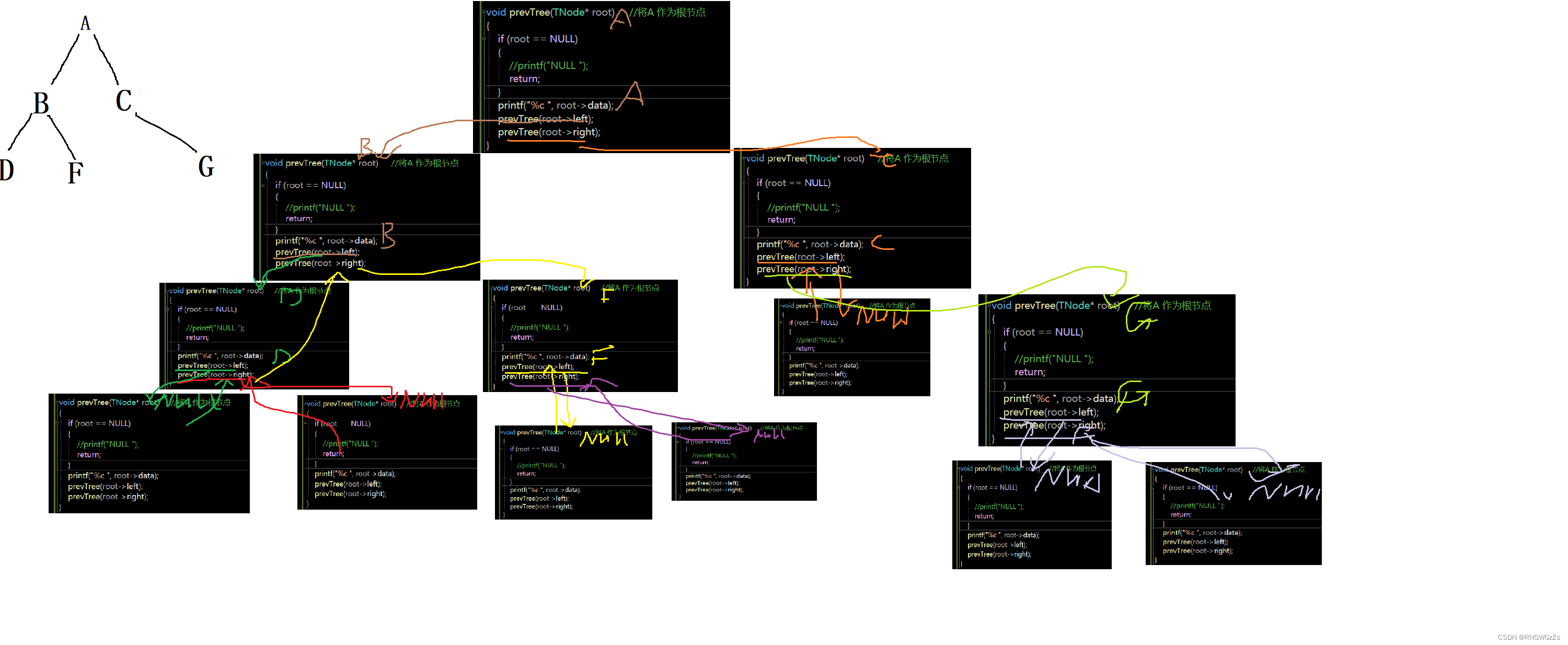
④中序和后序同上:

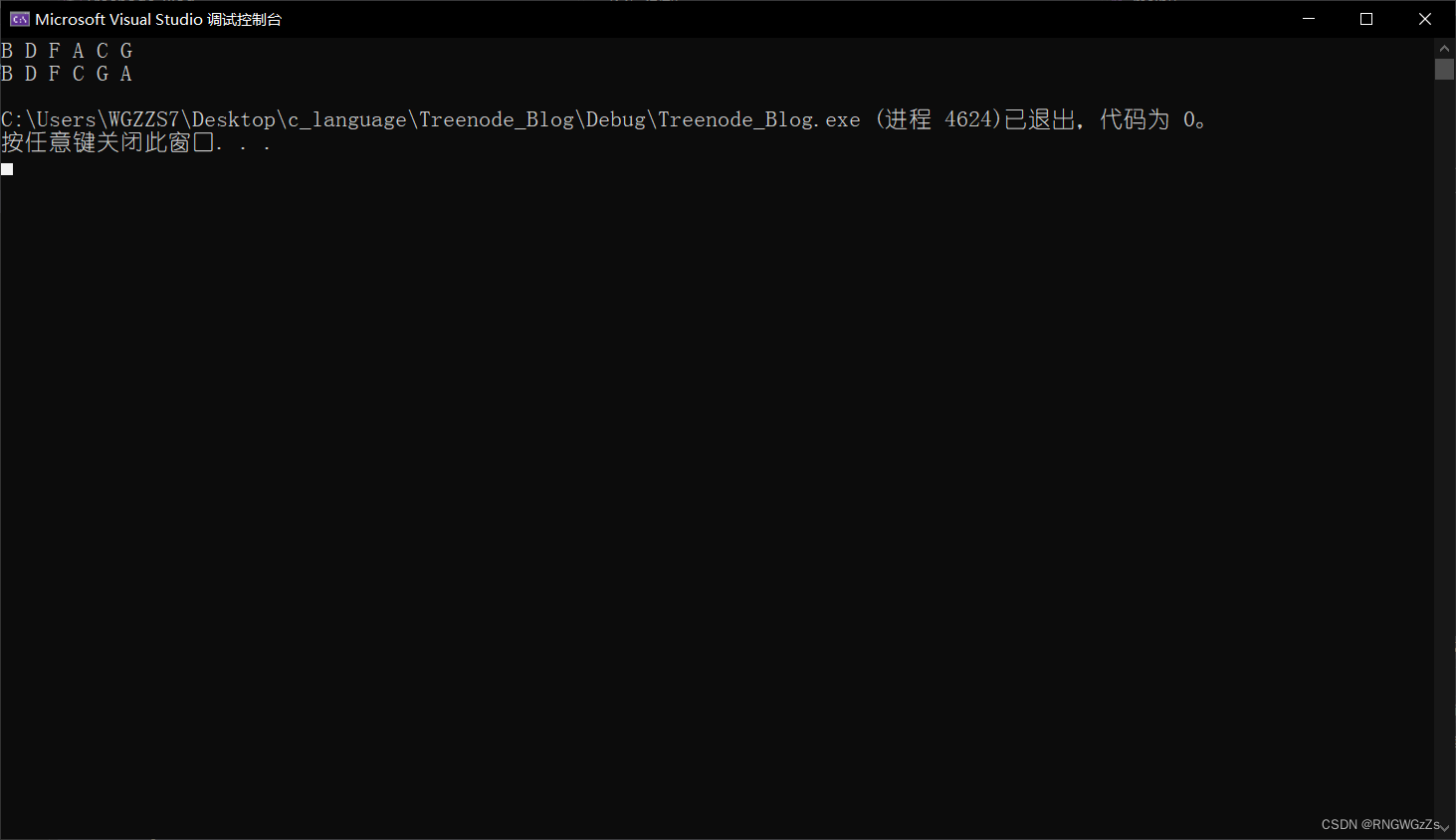 ⑤树的高度:

树中节点的最大层次

 

---

⑥树的节点个数:

两种不同写法，求树的节点个数。

以上就是基本的二叉树的内容，接下来上题吧~

(四) 二叉树的实战运用~

(1)单项选择题:

 (2)Oj实操题:

1. 二叉树的前序遍历：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

2. 二叉树的中序遍历：https://leetcode-c
n.com/problems/binary-tree-inorder-traversal/

3. 二叉树的后序遍历：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/

4. 二叉树的最大深度：https://leetc4ode-cn.com/problems/maximum-depth-of-binary-tree/

5. 平衡二叉树：https://leetcode-cn.com/problems/balanced-binary-tree/

6. 二叉树遍历:https://www.nowcoder.com/questionTerminal/4b91205483694f449f94c179883c1fef

(五)例题分析

1.二叉树的前序遍历:

 

题目的要求是，对二叉树进行前序遍历，然后返回数组。

遍历二叉树前，就要知道这个二叉树有几个节点>

  

并动态开辟出一个数组，来存放二叉树的值

 

重点就是 &i 和 i 也就是传址、传值的区别:

因为对数组的控制仅用的一个i 变量，用传址的方式，控制数组下标>_

2~3.二叉树中序、后序遍历也如上面的那样，也就不多赘述

中序:

 后序：

 4.二叉树的最大深度:

在二叉树的基本实现里面，也对二叉树深度的代码进行了实现:

核心问题还是:左右子树的最大值+1；

 5.平衡二叉树

从题目的要求来看，对平衡二叉树给出的定义:高度差不超过1。

提到二叉树的高度，幸好前面有实现求树的高度的函数：

 

我们先对根的左右子树，算出深度，再相减。

 

6.遍历二叉树:

在做这个题之前，你是否能还原出下面图示的二叉树？

 

 

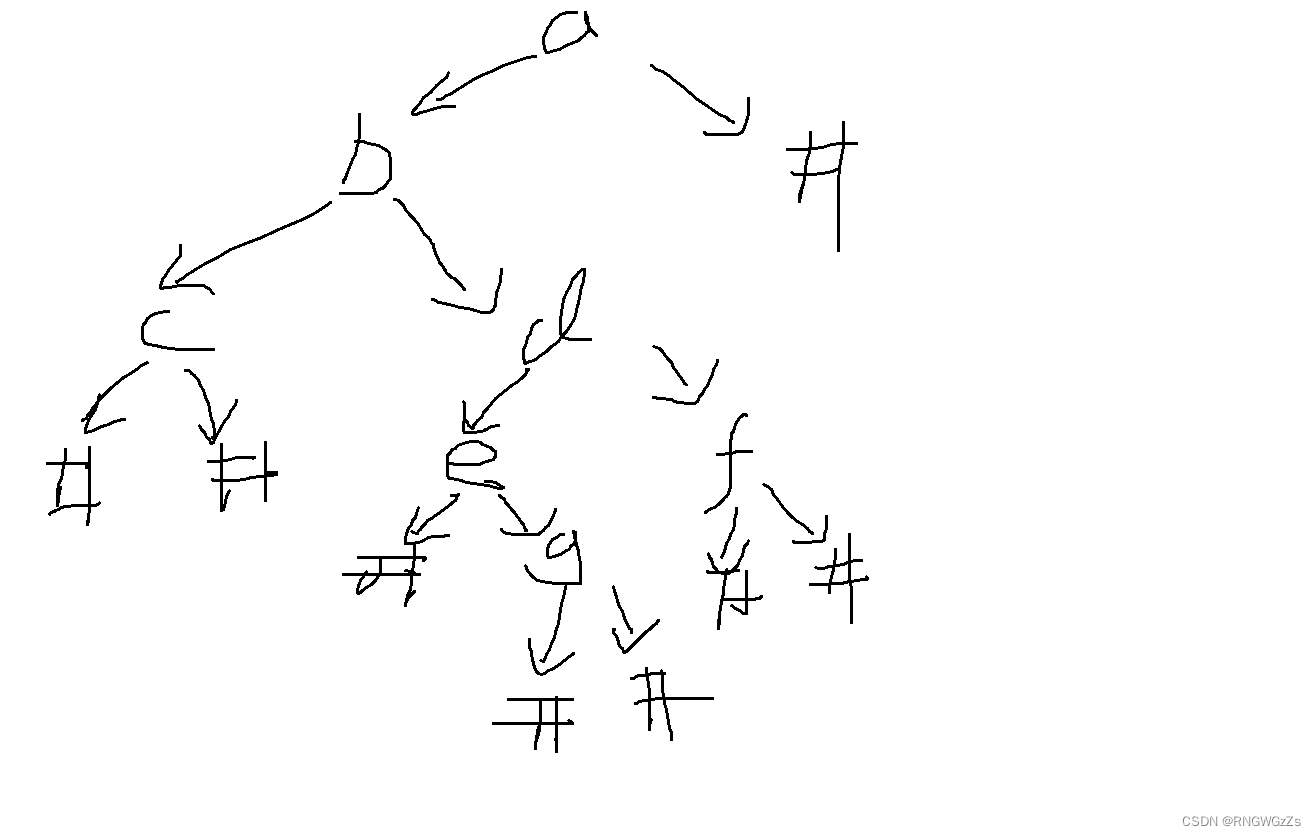
有了这个基础就可以开始做题啦~

(1)先创建节点:

 

data用来保存 用户输入的字母

(2)造树

 

用户录入字符串，根据字符串str 的内容构造树>

 

 

当然最后别忘了，中序输出~

这次的树、二叉树的总结就到这里啦，谢谢你的阅读。