二分的绝妙板子，闭区间寻找

递增三元组：

 

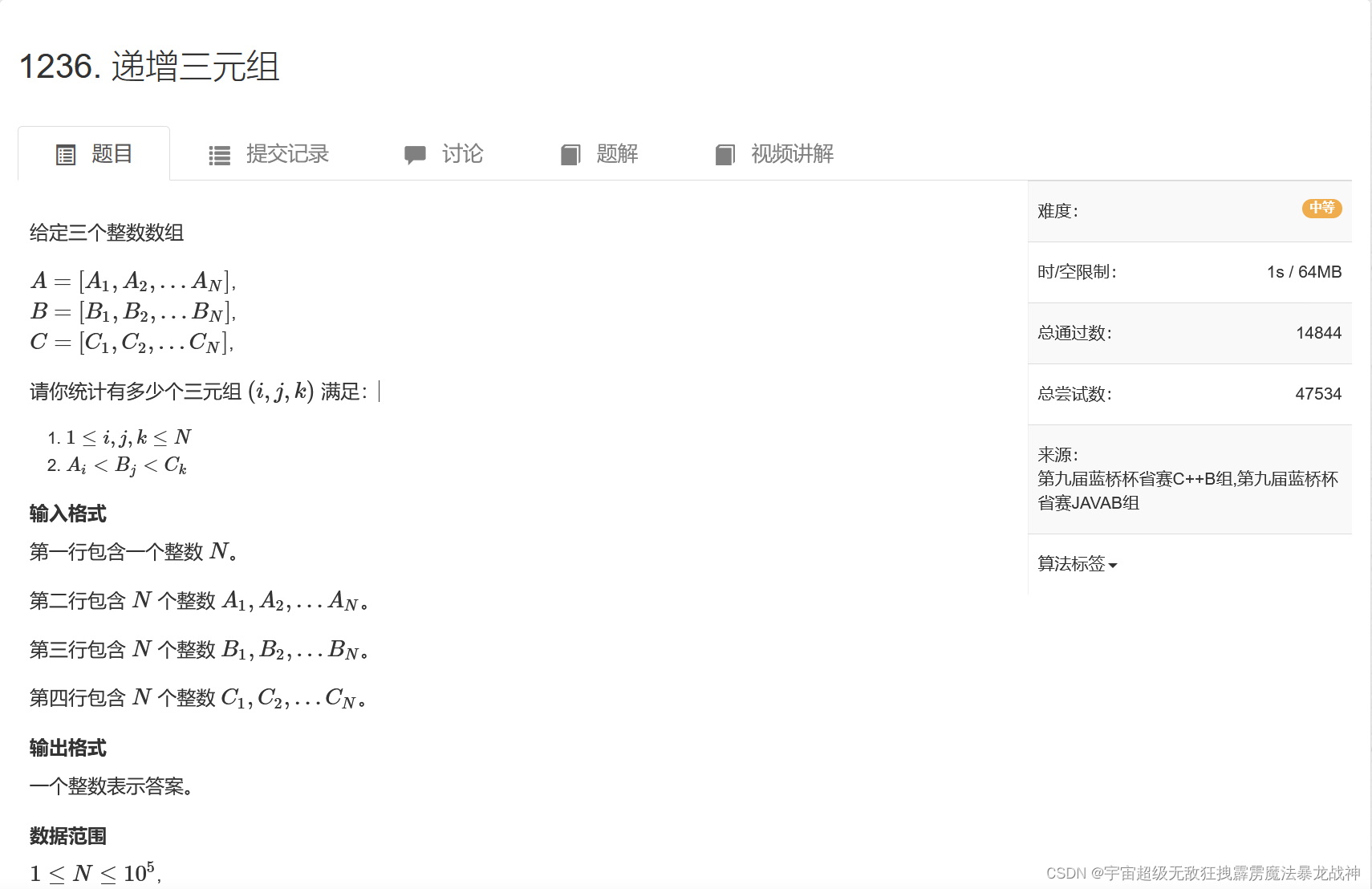
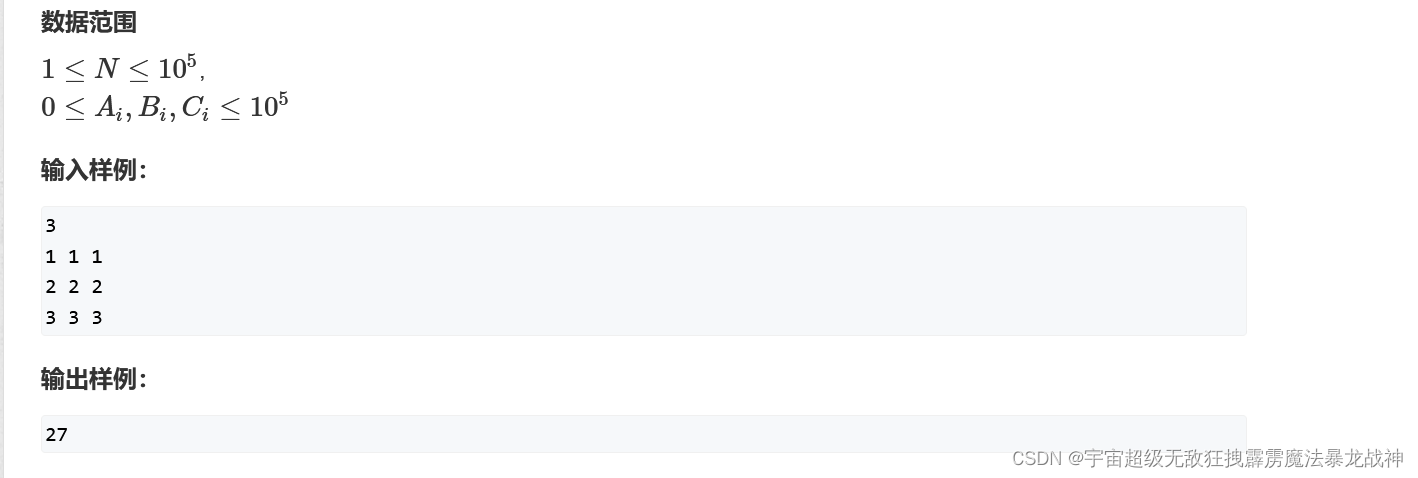
思路：

1、对3个数组分别进行从小到大排序

2、找到a[]数组中最小的大于等于bi的元素位置la，便可知小于bi的个数为num1

3、找到c[]数组中最大的小于等于bi的元素位置lb，便可知大于bi的个数为num2

4、由于a[]和c[]互斥，通过乘法原理可知符合条件的个数为num1 * num2
注意：当la == 0 或者 lb == n + 1时，则表示不符合条件

 

AC代码：（太优雅了）

import java.io.*;
import java.math.BigInteger;
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.*;
import java.util.stream.Collectors;

public class Main
{
    static PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static math math_bag = new math();
    static int N = (int)1e5 + 10;
    static int a[] = new int[N];
    static int b[] = new int[N];
    static int c[] = new int[N];

    static int n;

    // 二分的绝妙板子，闭区间寻找
    // 寻找左端点,
    static int findleft(int l, int r, int x)
    {
        while(l <= r)
        {
            int mid = l + r >> 1;
            if(a[mid] == x)  r = mid - 1;
            else if(a[mid] > x)  r = mid - 1;
            else l = mid + 1;
        }
        return r + 1;  // 找到的时候，r = mid - 1被多执行一次，所以要return r + 1;
    }

    // 寻找右端点
    static int findright(int l ,int r, int x)
    {
        while(l <= r)
        {
            int mid = (l + r) / 2;
            if(c[mid] == x) l = mid + 1;
            else if(c[mid] > x) r = mid - 1;
            else l = mid + 1;
        }
        return l - 1;  // 找到的时候，l = mid + 1被多执行一次，所以要return l - 1;
    }

    public static void main(String[] args ) throws IOException, ParseException
    {
        n = rd.nextInt();
        for(int i = 0 ; i < n ; i ++)  a[i] = rd.nextInt();
        for(int i = 0 ; i < n ; i ++)  b[i] = rd.nextInt();
        for(int i = 0 ; i < n ; i ++)  c[i] = rd.nextInt();

        Arrays.sort(a,0,n);
        Arrays.sort(b,0,n);
        Arrays.sort(c,0,n);

        long res = 0;
        for(int i = 0 ; i < n ; i ++)
        {
            int left = findleft(0,n - 1,b[i]); 
            int right = findright(0,n - 1,b[i]);

            res += (long)(left) * (n - right - 1); // left表示小于b[i]的数量，n - right - 1表示大于b[i]的数量，依据乘法原理，每个b[i]能构成的逆序对的数量为(left) * (n - right - 1)
        }
        pw.println(res);
        pw.flush();
    }
}

class rd
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");

    static String nextLine() throws IOException { return reader.readLine(); }
    static String next() throws IOException
    {
        while(!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }
    static int nextInt() throws IOException { return Integer.parseInt(next()); }
    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    static long nextLong() throws IOException { return Long.parseLong(next()); }
    static BigInteger nextBigInteger() throws IOException
    {
        BigInteger d = new BigInteger(rd.nextLine());
        return d;
    }
}

class math
{
    int gcd(int a,int b)
    {
        if(b == 0)  return a;
        else return gcd(b,a % b);
    }

    int lcm(int a,int b)
    {
        return a * b / gcd(a, b);
    }

    // 求n的所有约数
    List get_factor(int n)
    {
        List<Long> a = new ArrayList<>();
        for(long i = 1; i <= Math.sqrt(n) ; i ++)
        {
            if(n % i == 0)
            {
                a.add(i);
                if(i != n / i)  a.add(n / i);  // // 避免一下的情况：x = 16时，i = 4 ，x / i = 4的情况，这样会加入两种情况  ^-^复杂度能减少多少是多少
            }
        }

        // 相同因子去重，这个方法，完美
        a = a.stream().distinct().collect(Collectors.toList());

        // 对因子排序（升序）
        Collections.sort(a);

        return a;
    }

    // 判断是否是质数
    boolean check_isPrime(int n)
    {
        if(n < 2) return false;
        for(int i = 2 ; i <= n / i; i ++)  if (n % i == 0) return false;
        return true;
    }
}

class PII implements Comparable<PII>
{
    int x,y;
    public PII(int x ,int y)
    {
        this.x = x;
        this.y = y;
    }
    public int compareTo(PII a)
    {
        if(this.x-a.x != 0)
            return this.x-a.x;  //按x升序排序
        else return this.y-a.y;  //如果x相同，按y升序排序
    }
}

class Edge
{
    int a,b,c;
    public Edge(int a ,int b, int c)
    {
        this.a = a;
        this.b = b;
        this.c = c;
    }
}