94.旋转图像

一、题目描述

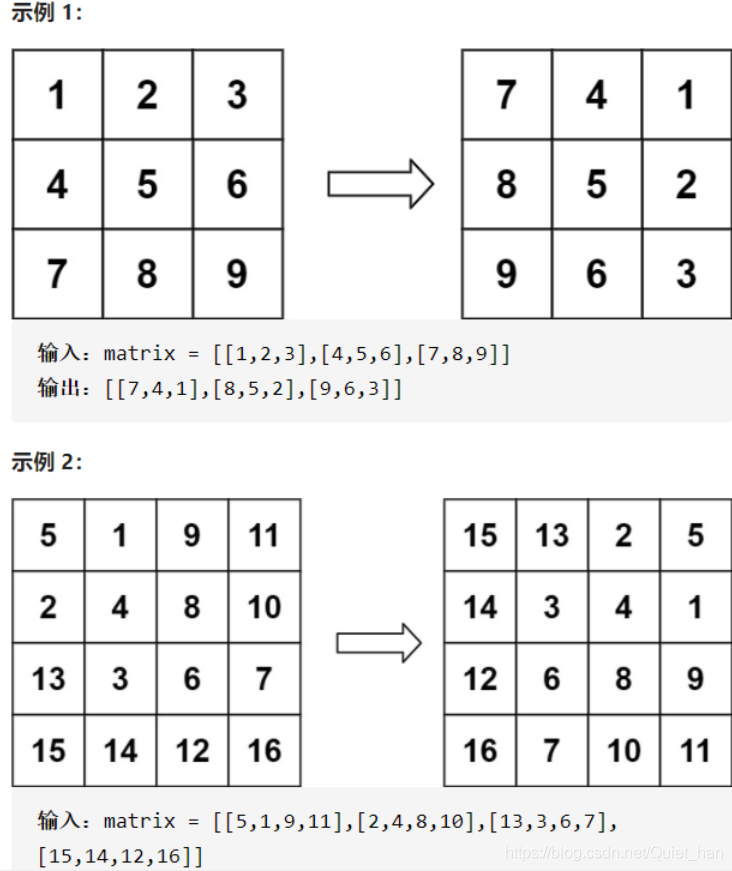
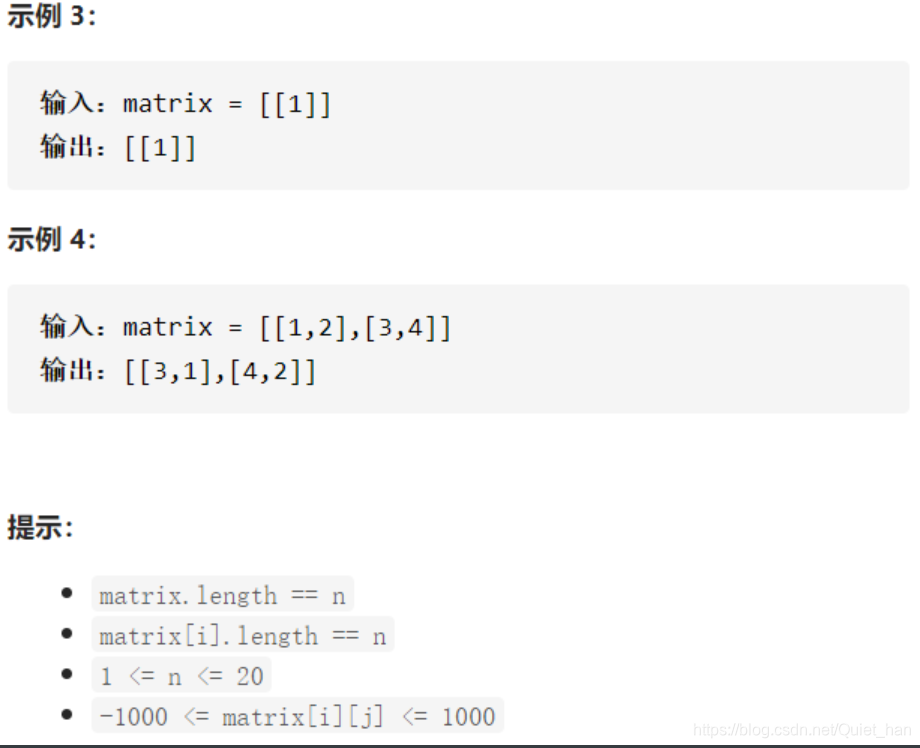
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

二、解题思路

方案一：

根据题目以示例1为例，通过坐标来分析一下旋转之后的图像坐标有没有什么规律呢？

对于第一个元素1，坐标是（0,0），旋转之后是（0,2）；

对于第二个元素2，坐标是（0,1），旋转之后是（1,2）；

对于第三个元素3，坐标是（0,2），旋转之后是（2,2）；

对于第四个元素4，坐标是（1,0），旋转之后是（0,1）；

通过这几个元素分析，你会发现对于每一个元素，它的纵坐标col会变成旋转之后的横坐标row。

那么每个元素旋转之后的纵坐标怎么归纳出来呢？每个矩阵都是n*n的，行列都是n，旋转之后的纵坐标可以总结出来是：n-row-1。来验证一下：

第一个元素纵坐标0，旋转之后是2，横坐标row=0，n-row-1 = 3-0-1=2，正确

第二个元素纵坐标是1，旋转之后是2，横坐标row=0，n-row-1 = 3-0-1=2，正确

所以最后可以总结出对于每个矩阵中的元素：matrix[row][col] = matrix[row][n-row-1]

下面我们通过一个例子来用这个式子模拟一下，会发现有趣的事情，假设给你如下图这么一个矩阵：

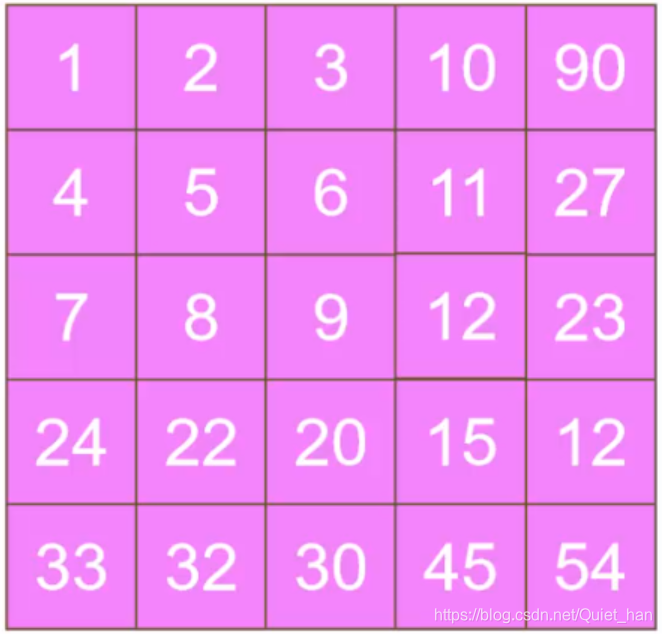
如图，我们以图中的元素6的旋转模拟，根据上面的公式matrix[row][col] = matrix[row][n-row-1]，元素6是需要旋转到坐标（2,3）的位置上，这里暂且让我将6的原始坐标表示成：[row(6)，col(6)]，转换之后6的坐标即是：

​ row(旋转6) = col(6)

​ col(旋转6) = n-row(6)-1

旋转之后的坐标（2,3）这个位置本身是有一个元素值12的，不能直接移过来覆盖掉，那继续通过公式来计算元素12这个值移动的位置：

[row(12)，col(12)]——>[col(12)，n-row(12)-1]

上面6移动过来的row(旋转6)和col(旋转6)正好就是row(12)，col(12)，那么就有：

row(12) = row(旋转6) = col(6)

col(12) = col(旋转6) = n-row(6)-1

带入到上面求12的旋转之后位置的公式会发现有：

[row(12)，col(12)]——>[n-row(6)-1，n-col(6)-1]

看到这里感觉有一丝丝复杂，其实就是将12这个元素值旋转之后的坐标用元素6的原始坐标表示出来做了一个替换而已。

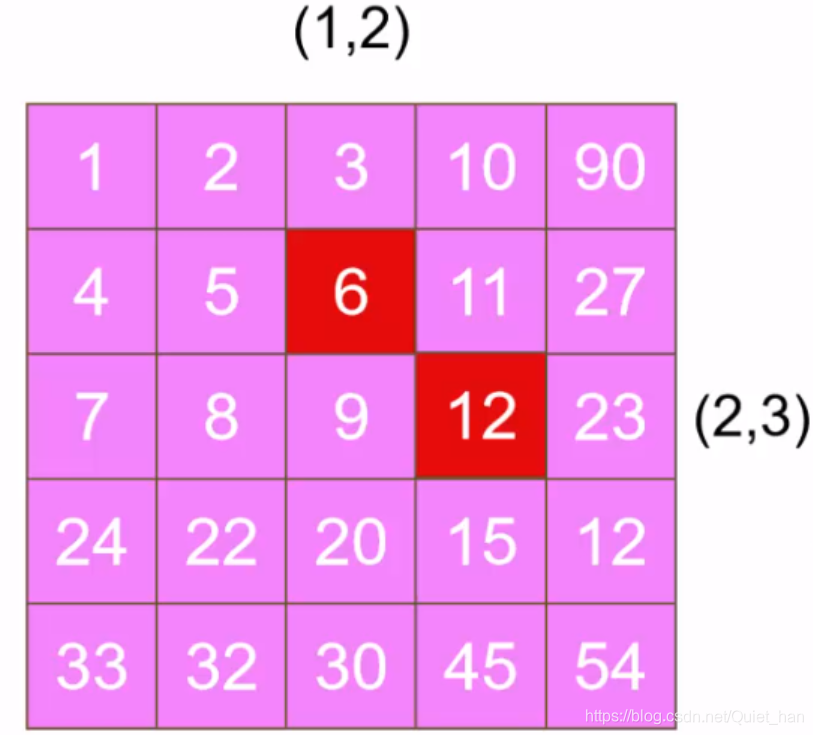
还的继续往下看，对于12的坐标（2,3）它旋转之后的坐标是（3,2），但是（3,2）这个坐标的位置上也有一个元素20，也是不能直接覆盖掉的，那么我们就先看看20这个元素它移动到哪里去了。还是根据公式来计算：

[row(20)，col(20)]——>[col(20)，n-row(20)-1]

上面已经计算过12移动之后的位置坐标就是20这个元素的初始坐标，那么就应该有：

[row(20)，col(20)] = [n-row(6)-1，n-col(6)-1]

row(20) = n-row(6)-1

col(20) = n-col(6)-1

然后将它代入到20的坐标旋转公式里就有：

[row(20)，col(20)]——>[col(20)，n-row(20)-1] = [n-col(6)-1，n-(n-row(6)-1)-1]

化简之后就变成了：[row(20)，col(20)]——>[n-col(6)-1，row6()]

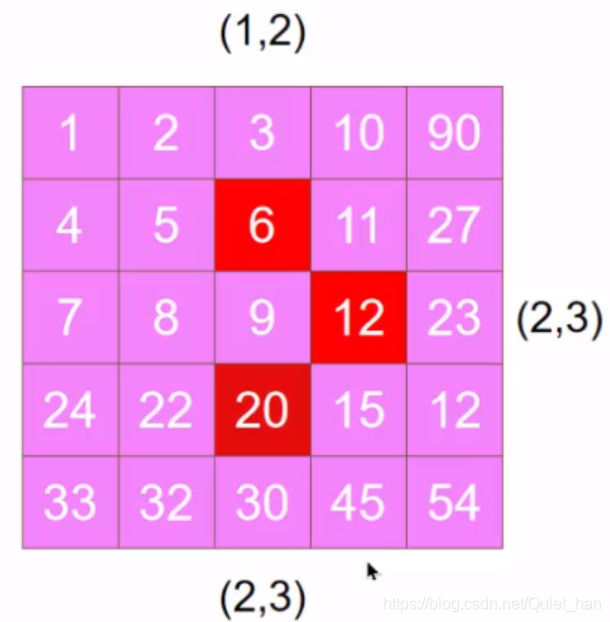
我们继续往下看，元素20旋转之后的坐标是（2,1），这个位置有一个元素是8，继续来看8旋转之后的位置通过公式：

[row(8)，col(8)]——>[col(8)，n-row(8)-1]

通过上面知道元素8的坐标是元素20旋转之后的坐标，就有：

row(8) = n-col(6)-1

col(8) = row(6)

然后代入转换公式有：[row(8)，col(8)]——>[row(6)，col(6)]

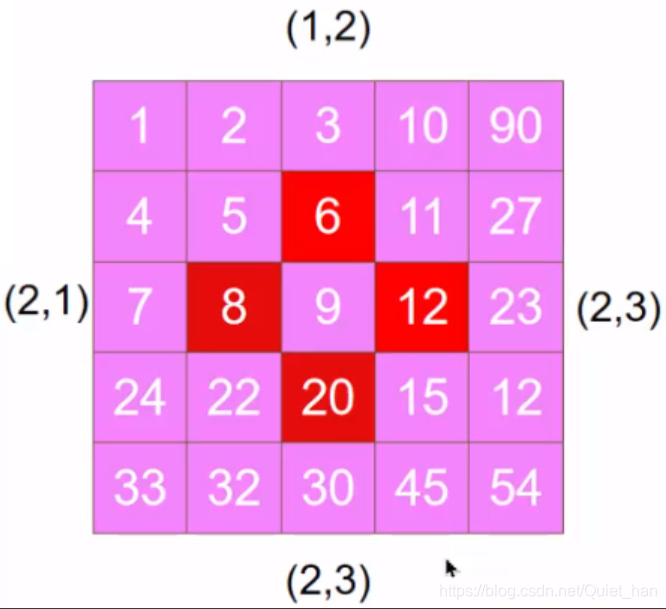
这时就能发现：6，12，20，8这几个元素旋转后形成一个循环，转了一圈。

下面通过分两种情况，n为偶数和n为奇数时。

当n为偶数时：

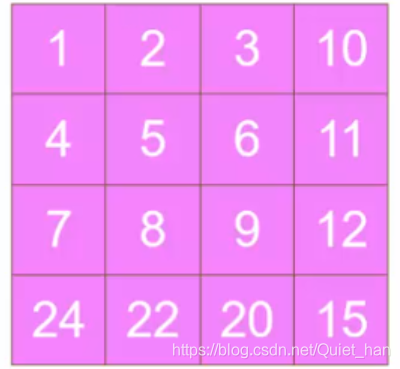
整个数组有n*n个元素，每次可以将4个元素放到相应位置上，那么就需要(n^2)/4将其拆分成(n/2)*(n/2)其中行坐标和列坐标各占一半，来看看什么意思呢：

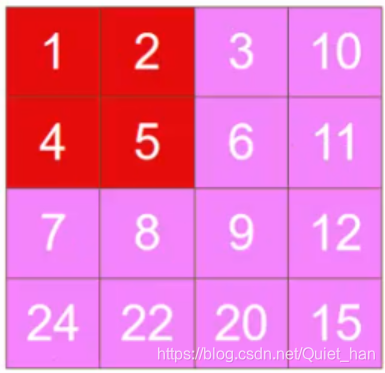
我们自己关注上图四个元素1，2，4，5：

• 当1作为起始元素时，上面的1，10，15，24作为一组，转一圈换位置

• 当2作为起始元素时，上面的2，11，20，7作为一组，转一圈换位置

• 当4作为起始元素时，上面的4，3，12，22作为一组，转一圈换位置

• 当1作为起始元素时，上面的5，6，8，9作为一组，转一圈换位置

  在每一组中其他元素的旋转之后额坐标都可以用起始元素的坐标表示出来的，这个上面已经推导过了，这几个元素的横纵坐标正好是n/2。

当n为奇数时：

会发现中间的元素不用动，需要遍历的元素有（n^2-1）/4 = ((n-1)/2)((n+1)/2)个，比如下面的矩阵只需要关注两行三列就行，这里就不一一列举啦。

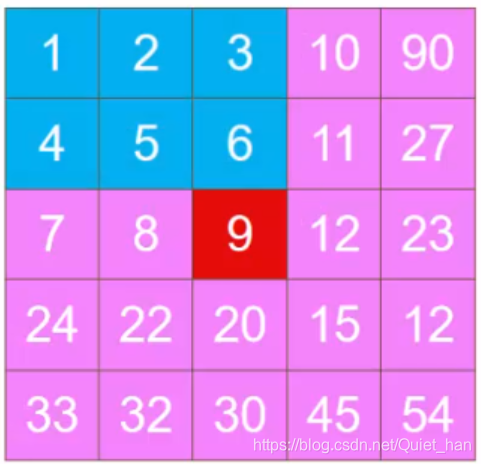
旋转模块如下：相当于就是蓝色到紫色那里，紫色到青色，青色旋转到黑色那里，黑色到蓝色。

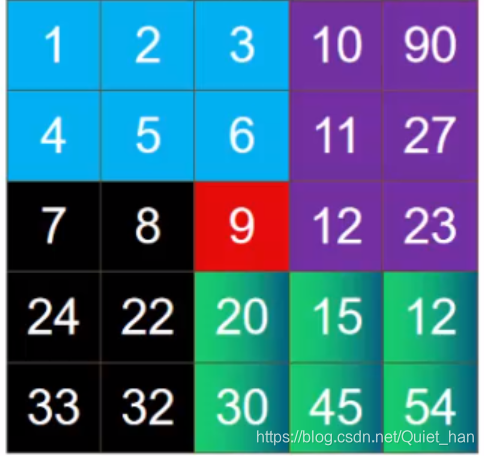
不管奇数还是偶数遍历情况如下，假设n是一个奇数，那么对于row来说，实际上(n-1)/2 = n/2。

对于列坐标col，当n是偶数时，n/2 = (n+1)/2，(java里面的整型除法舍去了小数)

for(int row=0; row<n/2; row++){
    for(int col=0; col<(n+1)/2; col++){
}

方案二：

原地翻转，先将矩阵水平翻转，再主对角线翻转

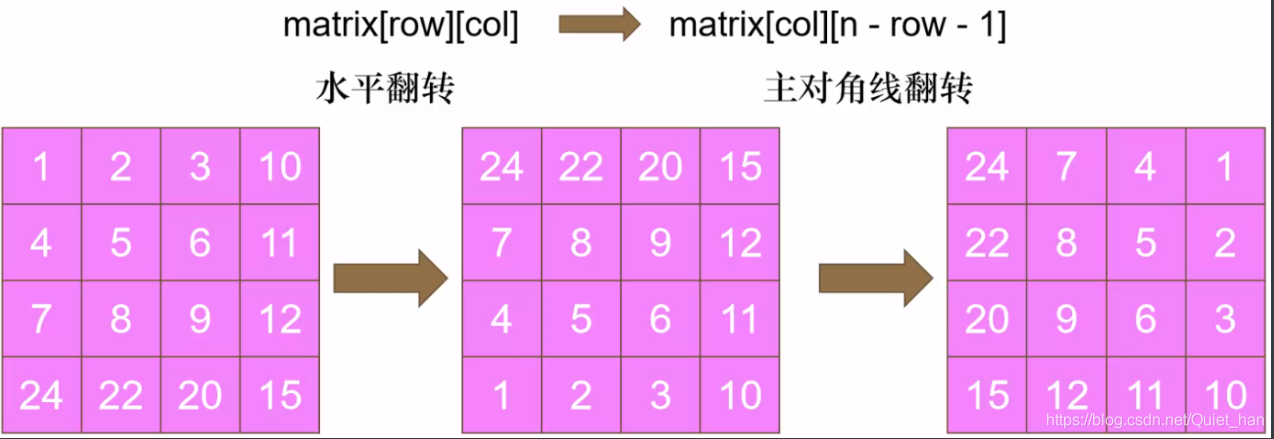
每次翻转坐标变化：

matrix[row][col]——>maxtrix[n-row-1][col]——>maxtrix[col][n-row-1]

三、代码演示

方案一：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for(int row=0; row<n/2; row++){
            for(int col=0; col<(n+1)/2; col++){
                //这里以上面的例子来说明（6,12,20,8）。先用一个变量存储6的坐标
                int tmp = matrix[row][col];
                //将8旋转到6的位置
                matrix[row][col] = matrix[n-col-1][row];
                //将20旋转到8的位置
                matrix[n-col-1][row] = matrix[n-row-1][n-col-1];
                //将12旋转到20的位置
                matrix[n-row-1][n-col-1] = matrix[col][n-row-1];
                //将6旋转到20的位置
                matrix[col][n-row-1] = tmp;
            }
        }
    }
}

时间复杂度：O（n^2）

空间复杂度：O（1）

方案二：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;

        //水平翻转
        for (int row=0; row<n/2; row++){
            for (int col=0; col<n; col++){
                int tmp = matrix[row][col];
                matrix[row][col] = matrix[n-row-1][col];
                matrix[n-row-1][col] = tmp;
            }
        }
        //主对角线旋转
        for (int row=0; row<n; row++){
            for (int col=0; col<row; col++){
                int tmp = matrix[row][col];
                matrix[row][col] = matrix[col][row];
                matrix[col][row] = tmp;
            }
        }
    }
}