92.转置矩阵

最新推荐文章于 2023-04-19 19:15:45 发布

原创最新推荐文章于 2023-04-19 19:15:45 发布 · 422 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

LeetCode刷题笔记专栏收录该内容

107 篇文章

订阅专栏

这篇博客详细介绍了如何实现矩阵的转置操作。通过直接模拟矩阵坐标交换的过程，创建一个新矩阵来存储转置后的结果。代码演示部分展示了一个Java方法，该方法接受一个二维整数数组作为输入，返回转置后的矩阵。这种方法简单直观，适用于处理各种大小的矩阵。

文章目录

二、题目描述
二、解题思路
三、代码演示

二、题目描述

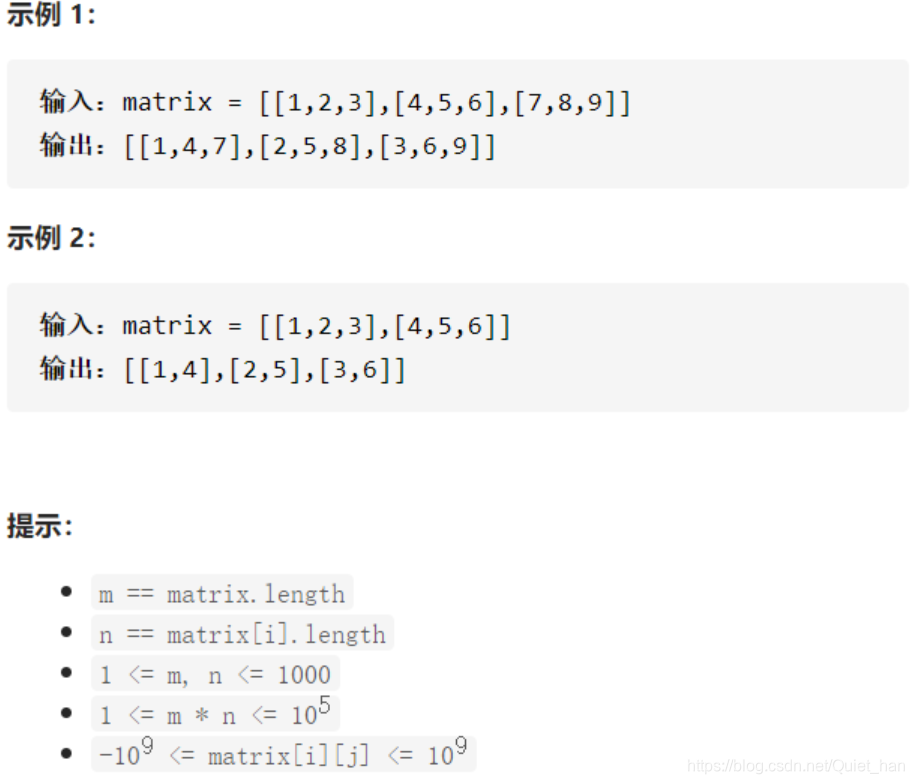
给你一个二维整数数组 matrix，返回 matrix 的 转置矩阵 。

矩阵的转置是指将矩阵的主对角线翻转，交换矩阵的行索引与列索引。
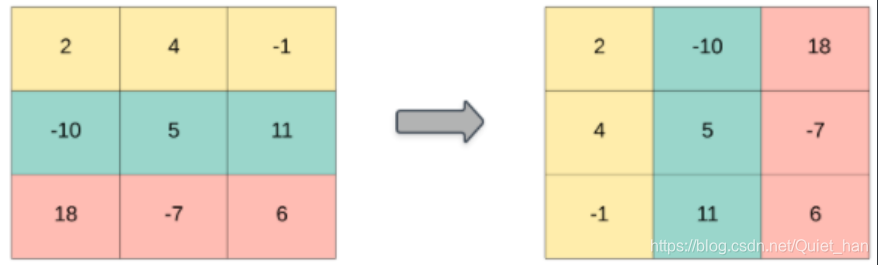
在这里插入图片描述

二、解题思路

方法：直接模拟

矩阵的转置就是将矩阵中每个元素的行列坐标交换生成该元素新的坐标，对于一个m*n的矩阵，它的转置矩阵就是n*m，求一个矩阵的转置矩阵之前先应该申请一个矩阵：
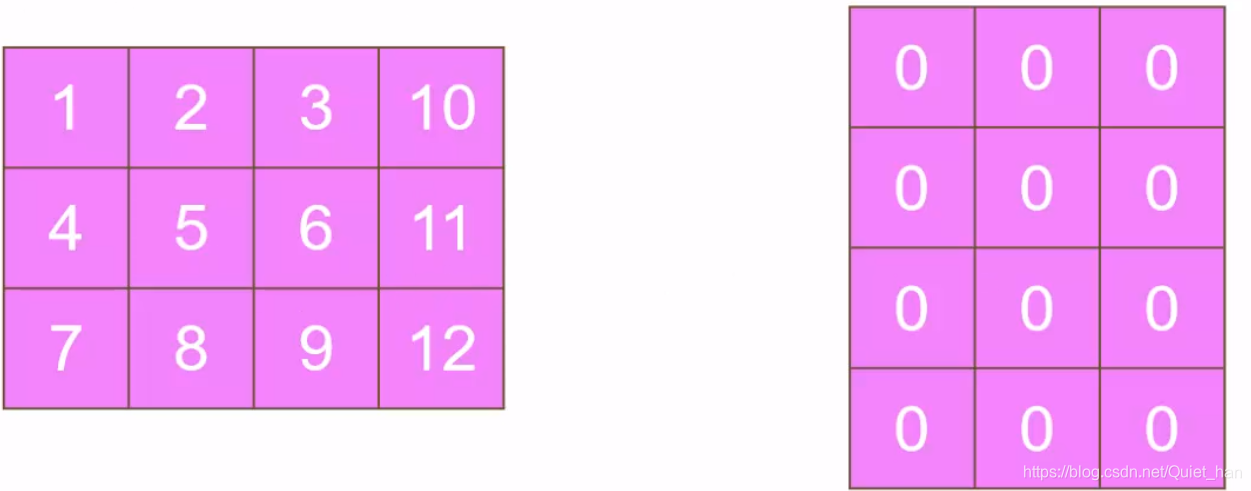
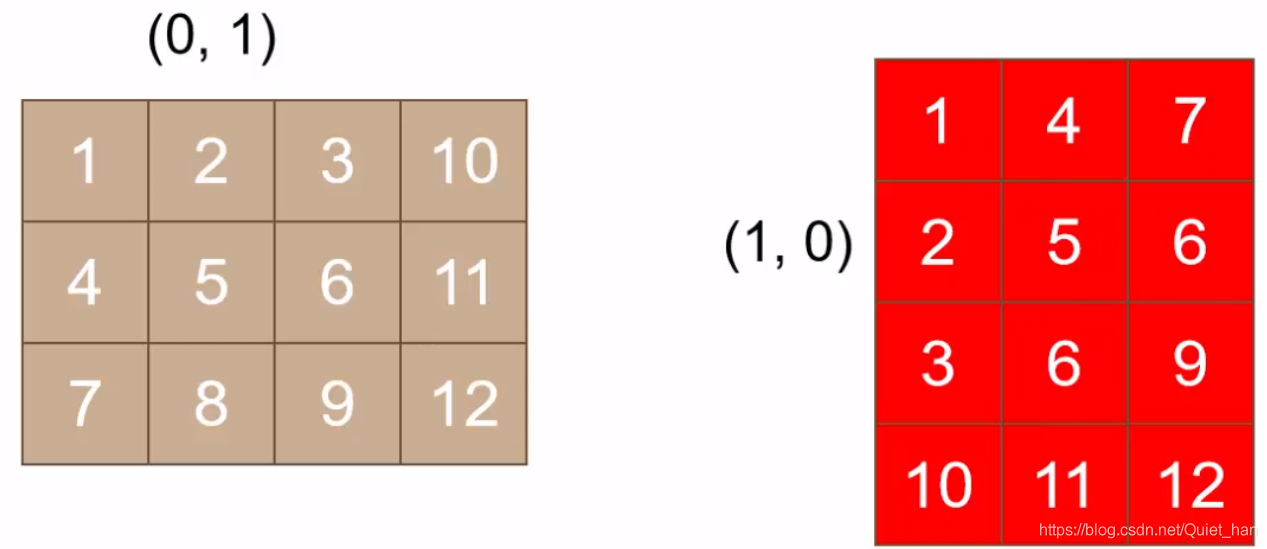
在这里插入图片描述
先来看第一个元素1坐标（0，0），转置之后坐标仍是（0，0），所以不变，对于第二个元素2，对应坐标是（1，0），转置之后坐标是（0，1），如下：

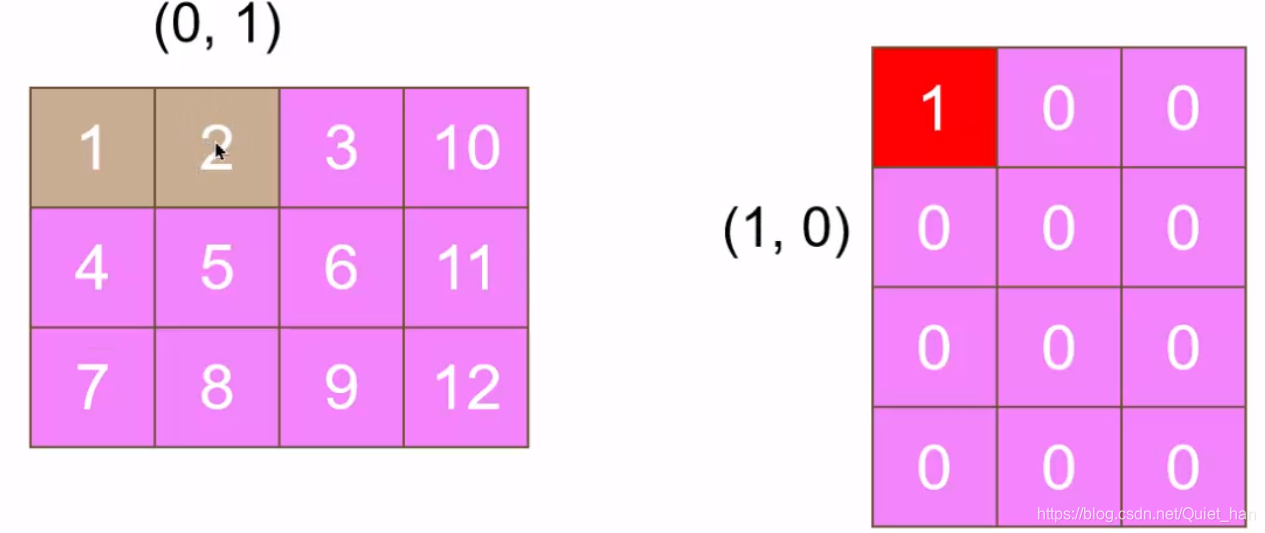
根据上面的步骤依次类推每个元素：

在这里插入图片描述

三、代码演示

class Solution {
    public int[][] transpose(int[][] matrix) {
        //矩阵的行数
        int m = matrix.length;
        //矩阵的列数：第一行的长度
        int n = matrix[0].length;

        //申请一个二维数组，存放原始矩阵转置之后的矩阵
        int[][] t = new int[n][m];

        //遍历原始数组
        for (int i=0; i<m; i++){
            for (int j=0; j<n; j++){
                t[j][i] = matrix[i][j];
            }
        }
    return t;
    }
}