【分治】hdu 1007

经典例题，平面最接近点对

题目

在一个二维平面上，有n个点，现在问最接近的两个点的距离是多少

思路

本来最近在练kd树的，想着上来就套个kd树。
但是很神奇的是kd树也给卡掉了。kd树的建树时间是$O(nlogn)$，二维的查询时间是$O(n * \sqrt(n))$
然后愉快的给卡数据量了orz。
刚好在上算法课，就写一下分治咯。

分治的思想：
对于平面上的点，我们先按照x轴给他们排序，从大问题划分成小问题。
当要比较的点小于等于三个的时候，直接暴力计算即可。
归并回来时，取左右区间的最小值。
那把两边合并后也会有点可以构造出较短的线段。

那当点数多的时候怎么办呢？
如果比较的点数可以使常数个的话，那就用不到$O(n ^ 2)$了对吧。

7次比较定理：

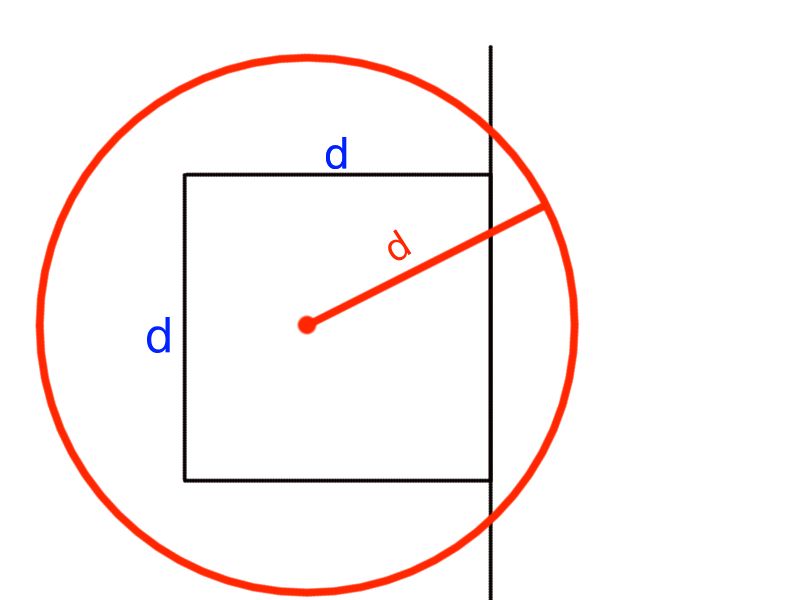
对于一个点，假设最短距离为d的时候，他在某点构成的图是这样的。
那么我们只要证明如果有一点他在中线上，那最多只要跟7个点进行比较即可。

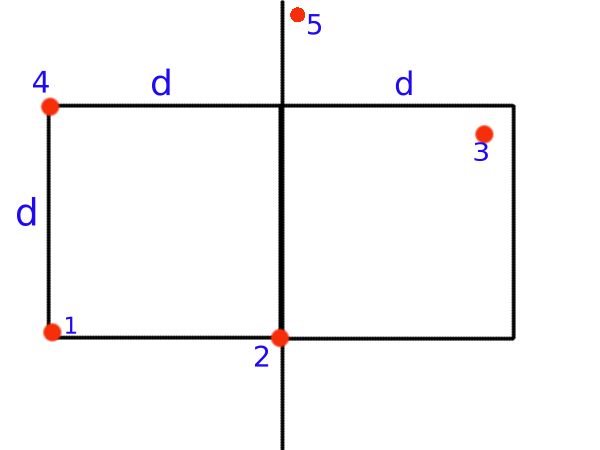
这里就不作几何了，我们不难发现，在2 * d * d的矩阵中，我们最多能发现有8个点他们两两之间距离不小于d

所以我们只需要划分一下中点左右界限为d的点集，再每次以高度为d的矩形来进行里面块的比较。
我们可以发现，一开始排序的时候按照x排序，分治完毕后，x轴好像并没有什么用了，我们可以想到归并排序，回溯的时候将y轴就顺带排序了。

下面给上代码：

/*
@resource: hdu 1007
@data: 2017-10-02
@author: QuanQqqqq
@algorithm: 分治
*/

#include <bits/stdc++.h>

#define MAXN 100005
#define INF (1LL << 30)

using namespace std;

struct Point {
    double x, y;
    bool operator < (const Point &a) const {
        return x < a.x;
    }
} pts[MAXN], tps[MAXN], ytps[MAXN];

double sqr(double x) {
    return x * x;
}

int cmpY(Point a, Point b) {
    return a.y < b.y;
}

double getDis(Point a, Point b) {
    return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
}

double findMinDisPoint(int L, int R) {
    double ret = INF;
    if (R - L <= 2) {
        for (int i = L; i <= R; i++) {
            for (int j = i + 1; j <= R; j++) {
                ret = min(ret, getDis(pts[i], pts[j]));
            }
            ytps[i] = pts[i];
        }
        //这里为了方便，只有三个数排序，依然是常数的时间复杂度
        sort(ytps + L, ytps + R + 1, cmpY);
        return ret;
    }
    int MID = L + R >> 1;
    double DL = findMinDisPoint(L, MID);
    double DR = findMinDisPoint(MID + 1, R);
    double d = min(DL, DR);
    ret = min(ret, d);
    //这里进行归并排序
    int idx = L, idxL = L, idxR = MID + 1;
    while (idxL <= MID && idxR <= R) {
        if (ytps[idxL].y <= ytps[idxR].y) {
            tps[idx++] = ytps[idxL++];
        } else {
            tps[idx++] = ytps[idxR++];
        }
    }
    while (idxL <= MID) {
        tps[idx++] = ytps[idxL++];
    }
    while (idxR <= R) {
        tps[idx++] = ytps[idxR++];
    }
    for (int i = L; i <= R; i++) {
        ytps[i] = tps[i];
    }

    //这里将距离大于的点筛除
    int cnt = 0;
    for (int i = L; i <= R; i++) {
        if (abs(ytps[i].x - ytps[MID].x) <= d) {
            tps[cnt++] = ytps[i];
        }
    }
    for (int i = 0; i < cnt; i++) {
        for (int j = i + 1; j < cnt && abs(tps[j].y - tps[i].y) < d; j++) {
            ret = min(ret, getDis(tps[i], tps[j]));
        }
    }
    return ret;
}

int main() {
    int n;
    while (~scanf("%d", &n) && n) {
        for (int i = 0; i < n; i++) {
            scanf("%lf %lf", &pts[i].x, &pts[i].y);
        }
        sort(pts, pts + n);
        printf("%.2lf\n", findMinDisPoint(0, n - 1) / 2);
    }
}

再。弱弱的送上tle多次的kd树，如果有dalao能帮忙就评论下呗。

/*
@resource: hdu 1007
@data: 2017-09-29
@author: QuanQqqqq
@algorithm: kd树
*/

#include <math.h>
#include <algorithm>
#include <stdio.h>

#define MAXN 100005
#define lson l, mid - 1, root << 1
#define rson mid + 1, r, root << 1 | 1
#define ll long long

using namespace std;

int idx, m;

struct node {
    double f[3];
    int id;
    bool operator < (const node &a) const {
        return f[idx] < a.f[idx];
    }
} kd[MAXN << 2], data[MAXN];

int flag[MAXN << 2];
pair<double, node> res;

void build(int l, int r, int root, int dep) {
    if (l > r) {
        return ;
    }
    flag[root] = 1;
    flag[root << 1] = flag[root << 1 | 1] = -1;
    idx = dep % m;
    int mid = l + r >> 1;
    nth_element(data + l, data + mid, data + r + 1);
    kd[root] = data[mid];
    build(lson, dep + 1);
    build(rson, dep + 1);
}

double sqr(double x) {
    return x * x;
}

double getDis(node a, node b) {
    return sqr(a.f[0] - b.f[0]) + sqr(a.f[1] - b.f[1]);
}

void query(node que, int root, int dep) {
    if (flag[root] == -1) {
        return ;
    }
    int x = root << 1;
    int y = root << 1 | 1;
    int idm = dep % 2;
    if (que.f[idm] >= kd[root].f[idm]) {
        swap(x, y);
    }
    if (~flag[x]) {
        query(que, x, dep + 1);
    }
    pair<double, node> cur = make_pair(getDis(que, kd[root]), kd[root]);
    bool mark = false;
    if (res.first == -1) {
        if (que.id != cur.second.id) {
            res.first = cur.first;
            res.second = cur.second;
        }
        mark = true;
    } else {
        if (cur.first < res.first && que.id != cur.second.id) {
            res.first = cur.first;
            res.second = cur.second;
        }
        //如果发现有可能作为最短距离进入看一下
        if (sqr(kd[root].f[idm] - que.f[idm]) < res.first) {
            mark = true;
        }
    }
    if (mark && ~flag[y]) {
        query(que, y, dep + 1);
    }
}

int main() {
    int T, n, q;
    m = 2;
    while (~scanf("%d", &n) && n) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                scanf("%lf", &data[i].f[j]);
            }
            data[i].id = i;
        }
        build(0, n - 1, 1, 0);
        res.first = -1;
        for (int i = 0; i < n; i++) {
            res.second = data[i];
            query(data[i], 1, 0);
        }
        printf("%.2lf\n", sqrt(res.first) / 2);
    }
    // system("pause");
}