C++学习：【PTA】7-1 实验4-1（二叉搜索树和平衡二叉树）

7-1 实验4-1（二叉搜索树和平衡二叉树）

用分别实现二叉搜索树和平衡二叉树的创建、插入和查找操作。

输入格式:
输入第一行是一个整数n，表示后面有n个整数按顺序分别插入一棵二叉搜索树和一棵平衡二叉树。例如：

3

10 20 30

表示分别向二叉搜索树和平衡二叉树按输入顺序插入3个结点，结点的元素值分别是10、20、30。因此，构建完成的二叉搜索树和平衡二叉树分别为：

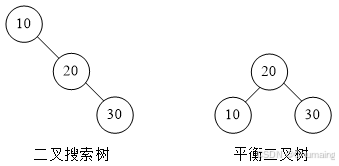
输出格式:
分别在两棵树中对所有元素执行查找操作，统计查找过程中进行比较的总次数，分两行输出。例如，对于上面的示例输入，输出为：

6

5

说明：第1行的6表示在二叉搜索树中，查找10这个元素需要比较1次，查找20这个元素需要比较2次，查找30这个元素需要比较3次，因此总共是6次；第2行的5表示在平衡二叉树中，查找10这个元素需要比较2次，查找20这个元素需要比较1次，查找30这个元素需要比较2次，因此总共是5次。

输入样例:
在这里给出一组输入。例如：

7

10 20 30 40 50 60 70

输出样例:
在这里给出相应的输出。例如：

28

17

代码长度限制 16 KB

时间限制 400 ms

内存限制 64 MB

栈限制 8192 KB

注：编译器选择C++

#include <stdlib.h>
#include <stdio.h>

typedef int ElementType;

/*----------------------平衡二叉树------------------------*/

typedef struct AVLNode* Position;
typedef Position AVLTree;  // AVL树类型
typedef struct AVLNode {
    ElementType Data;
    AVLTree Left;
    AVLTree Right;
    int Height;  // 树高
};

int Max(int a, int b) {
    return a > b ? a : b;
}

int GetHeight(AVLTree T) {
    if(T) return T->Height;
    return 0;
}

AVLTree SingleLeftRotation(AVLTree T);  // 左单旋
AVLTree DubleLeftRightRotation(AVLTree T);  // 左右双旋
AVLTree SingleRightRotation(AVLTree T);  // 右单旋
AVLTree DubleRightLeftRotation(AVLTree T);  // 右左单旋


AVLTree Insert(AVLTree T, ElementType X) {
    /* 将X插入AVL树T中，并且返回调整后的AVL树 */
    if (!T) {  // 若插入空树，则新建包含一个结点的树
        T = (AVLTree)malloc(sizeof(struct AVLNode));
        T->Data = X;
        T->Left = T->Right = NULL;
        T->Height = 1;  // 新结点高度是1
    }  // 插入空树结束

    else if (X < T->Data) {  // X将插入在T的左子树
        T->Left = Insert(T->Left, X);  // X插入T的左子树
        // 插入X完成，此时X在T的左子树
        if (GetHeight(T->Left) - GetHeight(T->Right) == 2)  // 如果需要左旋
            if (X < T->Left->Data)  // 满足左单旋
                T = SingleLeftRotation(T);
            else  // 满足右单旋
                T = DubleLeftRightRotation(T);
    }

    else if (X > T->Data) {  // X将插入T的右子树
        T->Right = Insert(T->Right, X);  // X插入T的右子树
        // 插入X完成，此时X在T的右侧
        if (GetHeight(T->Left) - GetHeight(T->Right) == -2)  // 如果需要右旋
            if (X > T->Right->Data)  // 满足右单旋
                T = SingleRightRotation(T);
            else  // 满足右左单旋
                T = DubleRightLeftRotation(T);
    }

    // else X == T->Data 无需插入

    T->Height = Max(GetHeight(T->Left), GetHeight(T->Right)) + 1;  // 更新树高
    return T;
}

AVLTree SingleLeftRotation(AVLTree A) {
    /*
     * 左单旋
     * 注意：A必须有一个左子结点B
     * 将AB左单旋，更新A与B的高度，返回新的根结点B
     */
    AVLTree B = A->Left;
    A->Left = B->Right;
    B->Right = A;
    A->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;
    B->Height = Max(GetHeight(B->Left), GetHeight(B->Right)) + 1;
    return B;
}

AVLTree SingleRightRotation(AVLTree A) {
    /*
     * 右单旋
     * 注意：A必须有一个右子结点B
     * 将AB右单旋，更新A与B的高度，返回新的根结点B
     */
    AVLTree B = A->Right;
    A->Right = B->Left;
    B->Left = A;
    A->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;
    B->Height = Max(GetHeight(B->Left), GetHeight(B->Right)) + 1;
    return B;
}

AVLTree DubleLeftRightRotation(AVLTree A) {
    /*
     * 左右双旋
     * 注意：A必须有一个左子结点B，且B必须有一个右子结点C
     * 左右单旋，返回新的根结点C
     */
    AVLTree B = A->Left;
    A->Left = SingleRightRotation(B);  // 将B与C右单旋，返回C
    return SingleLeftRotation(A);  // 将A与C左单旋，返回C
}

AVLTree DubleRightLeftRotation(AVLTree A) {
    /*
     * 右左双旋
     * 注意：A必须有一个右子结点B，且B必须有一个左子结点C
     * 右左单旋，返回新的根结点C
     */
    AVLTree B = A->Right;
    A->Right = SingleLeftRotation(B);  // 将B与C左单旋，返回C
    return SingleRightRotation(A);  // 将A与C右单旋，返回C
}

/*----------------------二叉搜索树------------------------*/
typedef struct TNode * BPosition;
typedef BPosition BinTree;
struct TNode {
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

BinTree Insert(BinTree BST, ElementType X) {
    if (!BST) {
        BST = (BinTree)malloc(sizeof(struct TNode));
        BST->Data = X;
        BST->Left = BST->Right = NULL;
    }
    else {
        if (X < BST->Data)
            BST->Left = Insert(BST->Left, X);
        else if (X > BST->Data)
            BST->Right = Insert(BST->Right, X);
    }
    return BST;
}

int FindCount(BinTree T, ElementType X) {
    int count = 0;
    while (T) {
        count ++;
        if (X > T->Data)
            T = T->Right;
        else if (X < T->Data)
            T = T->Left;
        else break;
    }
    return count;
}

int FindCount(AVLTree T, ElementType X) {
    int count = 0;
    while (T) {
        count ++;
        if (X > T->Data)
            T = T->Right;
        else if (X < T->Data)
            T = T->Left;
        else break;
    }
    return count;
}


int main(int argc, char *argv[]) {
    BinTree A = NULL;
    AVLTree B = NULL;
    int N, X, count1=0, count2=0;
    scanf("%d", &N);
    int a[N+1];
    for(int i = 0; i < N; i++) {
        scanf("%d", &X);
        A = Insert(A, X);
        B = Insert(B, X);
        a[i] = X;
    }

    for(int i = 0; i < N; i++) {
        count1 += FindCount(A, a[i]);
        count2 += FindCount(B, a[i]);
    }

    printf("%d\n%d", count1, count2);
}