python学习——洛谷[NOIP2001 普及组] 数的计算，两种方法详解

[NOIP2001 普及组] 数的计算

题目描述

给出正整数 $n$，要求按如下方式构造数列：

1. 只有一个数 $n$ 的数列是一个合法的数列。
2. 在一个合法的数列的末尾加入一个正整数，但是这个正整数不能超过该数列最后一项的一半，可以得到一个新的合法数列。

请你求出，一共有多少个合法的数列。两个合法数列 $a,b$ 不同当且仅当两数列长度不同或存在一个正整数 $i\le |a|$，使得 $a_i\ne b_i$。

输入格式

输入只有一行一个整数，表示 $n$。

输出格式

输出一行一个整数，表示合法的数列个数。

样例 #1

样例输入 #1

6

样例输出 #1

6

提示

样例 1 解释

满足条件的数列为：

• $6$
• $6,1$
• $6,2$
• $6,3$
• $6,2,1$
• $6,3,1$

数据规模与约定

对于全部的测试点，保证 $1\le n\le 10^3$。

说明

本题数据来源是 NOIP 2001 普及组第一题，但是原题的题面描述和数据不符，故对题面进行了修改，使之符合数据。原题面如下，谨供参考：

我们要求找出具有下列性质数的个数（包含输入的正整数 $n$）。

先输入一个正整数 $n$（$n\le 1000$），然后对此正整数按照如下方法进行处理：

1. 不作任何处理；
2. 在它的左边拼接一个正整数，但该正整数不能超过原数，或者是上一个被拼接的数的一半；
3. 加上数后，继续按此规则进行处理，直到不能再加正整数为止。

感谢 @dbxxx 对本题情况的反馈，原题面的问题见本贴。

分析

读题，先来找规律：可以看出，这是很明显的树状结构

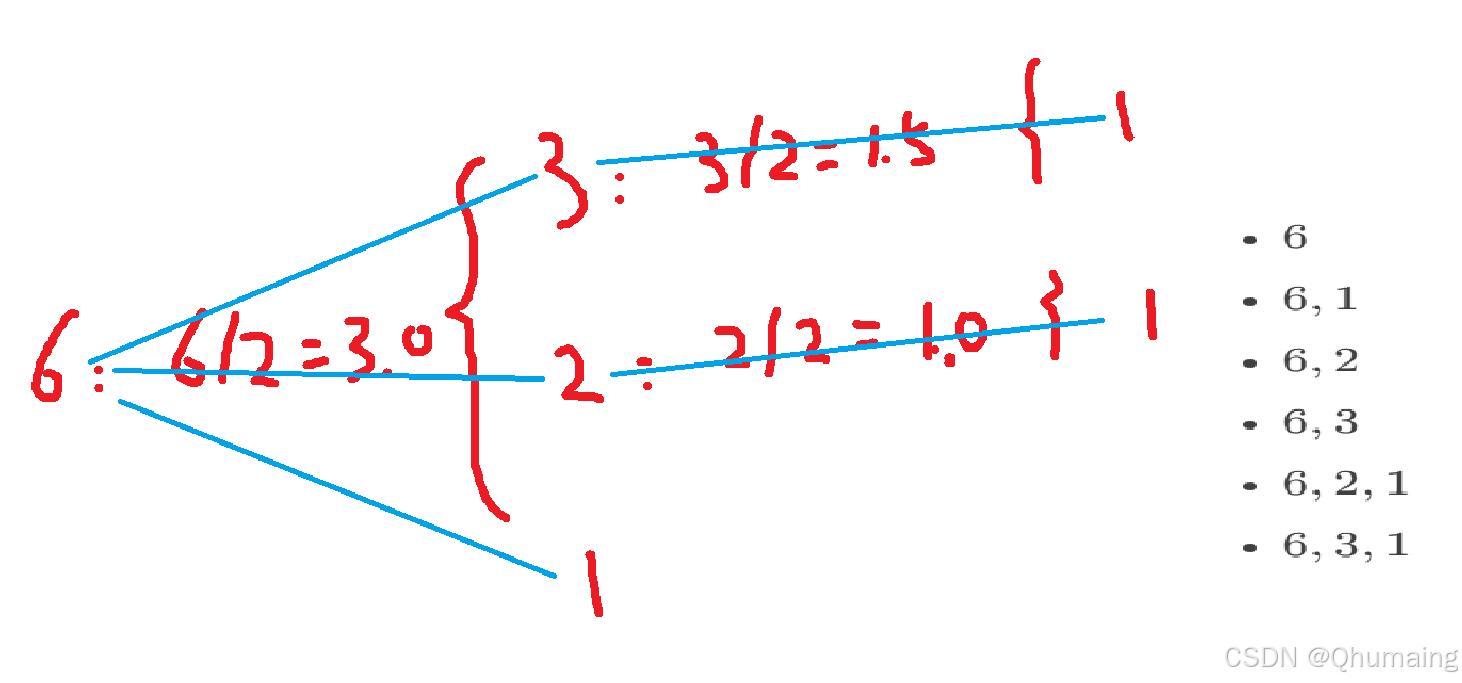
即：

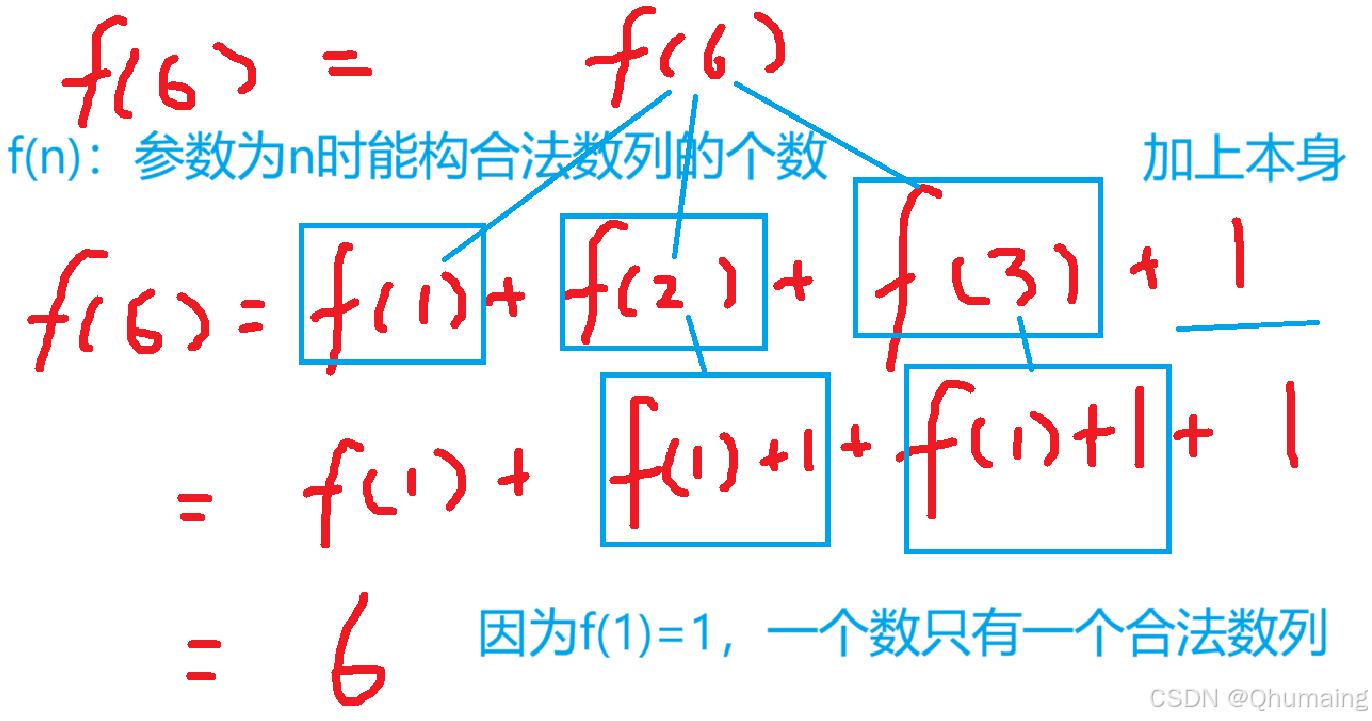
由上可以总结出以下公式：

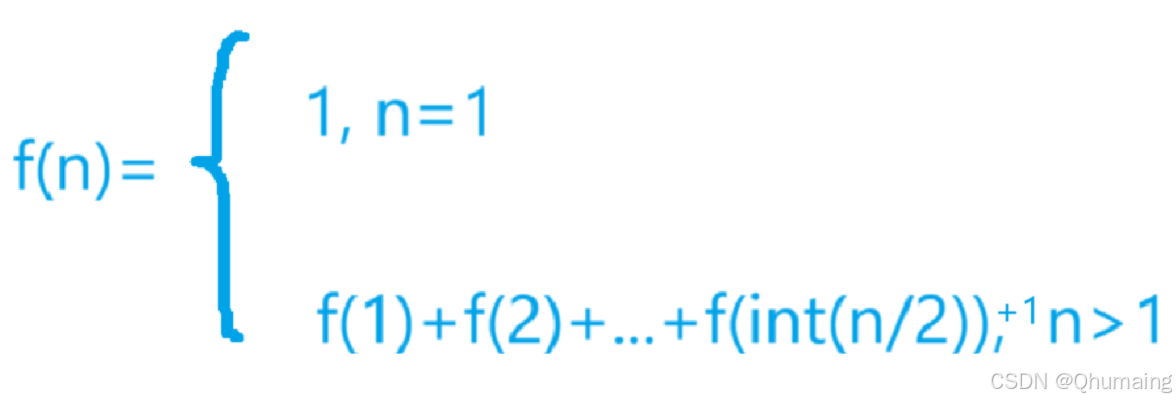
而对照

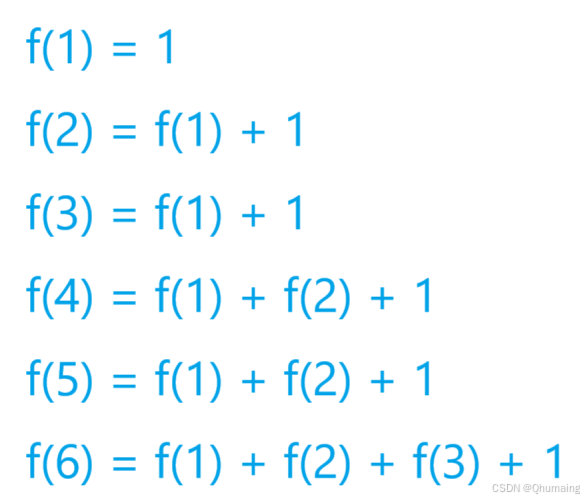
发现，这个公式是有缺陷的

因此最终的公式为：

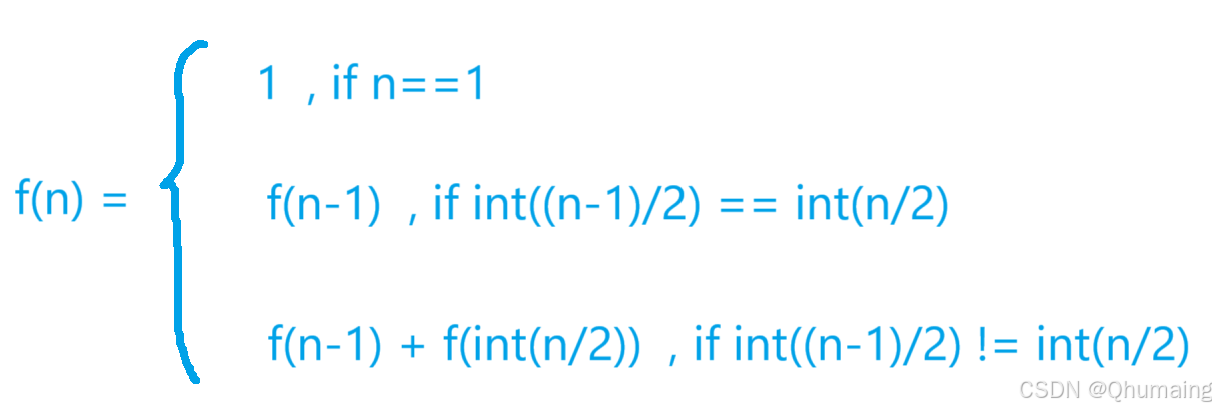
所以一开始很容易想到递归：

方法一（递归）

def f(n):
    if n == 1:
        return 1
    if(int(n/2) == int((n-1)/2)):
        return f(n-1)
    return f(n-1) + f(int(n/2))
print(f(int(input())))

但是递归有缺陷，就是每次算f(n)时，f(1) f(2) f(3) f(4)都要重新算一遍，时间复杂度为O(2^n)，很容易TE
因此我们需要想办法把前面算过的储存起来，避免不必要的计算
因此有了方法二：

方法二（dp问题）

n = int(input())
if n == 1:
    print(1)
else:
    f = {1:1}
    for i in range(2, n+1):
        if int(i / 2) == int((i - 1) / 2):
            f[i] = f[i - 1]
        else:
            f[i] = f[i - 1] + f[int(i / 2)]
    print(f[n])

这里我用了字典去存储，相比于列表，字典当key不存在时不会报错，而是创建一个新的key