因斯布鲁克大学发明一种更快的新型量子计算机

奇偶校验计算机可以在单个量子比特上执行两个或多个量子比特之间的操作，更容易实现复杂的算法。

该团队由 Wolfgang Lechner（右一）领导，包括Kilian Ender（右二）、Anette Messinger（左二） 和 Michael Fellner（左一）。图片来源：Erika Bettega (ParityQC)

在量子计算机中，量子比特 (qubits) 需要同时充当计算单元和内存。量子信息不能像传统计算机那样存储在内存中，因为它（根据量子不可克隆原理）无法复制。由于这一限制，量子计算机的量子比特必须能够相互发生交互作用，而这仍然是开发强大量子计算机的重大挑战。

为了克服这个问题，理论物理学家Wolfgang Lechner与Philipp Hauke和Peter Zoller在2015年提出了一种新颖的量子计算机架构。这种架构现在以作者的名字命名为LHZ架构。

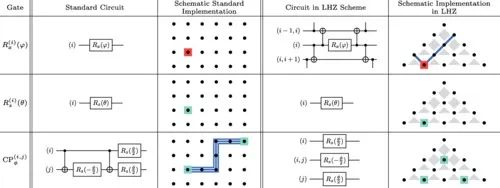
LHZ方案中通用门集的实现概述。所有操作都已分解为cnot门和局部旋转。蓝线代表一连串的cnot门，而红色（较深）和绿色（较浅）的方块分别表示局部RX和Rz旋转。三行对应交换门，每行由3个cnot门组成。

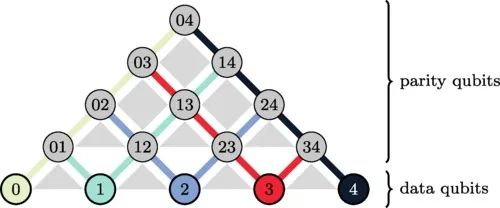
带有逻辑线的修改后的LHZ架构的插图。三体和四体约束由相应量子比特之间的浅灰色三角形和正方形表示。具有单个逻辑索引的数据量子比特被添加为架构底部的附加行，以允许直接访问逻辑Rz旋转。彩色线连接标签包含相同逻辑索引的所有量子比特。合乎逻辑RX旋转可以通过沿相应线的cnot门链来实现。

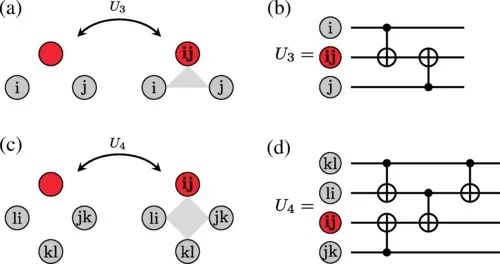
用于在代码中添加或删除量子比特和相应约束的编码和解码电路。(a) Qubit(ij)通过相邻的数据量子比特（i） 和 （j) 在三体约束中直接编码，对应量子电路为 (b)。(c) Qubit(ij)使用四体约束中的其他奇偶校验量子比特进行编码，对应量子电路 (d)。没有标签的量子比特表示没有任何奇偶校验信息的量子比特，处于状态|0〉。

“这种架构最初是为优化问题而设计的，”奥地利因斯布鲁克大学理论物理系的 Wolfgang Lechner 回忆道。“在此过程中，我们将架构缩小到最低限度，以便尽可能高效地解决这些优化问题。”

该架构中的物理量子比特包含了量子比特之间的相对协调信息，而不仅仅表示单个比特。

“这意味着并非所有量子比特都必须再相互作用了。”Wolfgang Lechner 解释道。他和他的团队现在已经表明，这种奇偶校验概念也适用于通用量子计算机。

简化复杂操作

奇偶校验计算机可以在单个量子比特上执行两个或多个量子比特之间的操作。“现有样机已经在小规模上很好地实现了这样的操作，”Wolfgang Lechner团队的Michael Fellner表示。

“然而，随着量子比特数量的增加，实现这些门操作变得越来越复杂。”

在Physical Review Letters和Physical Review A的两篇出版物中，因斯布鲁克的科学家们证明，奇偶校验计算机可以执行量子傅里叶变换——许多量子算法的基本构建块——而且由于计算步骤明显减少，因此速度更快。

“我们架构的高度并行性意味着，可以非常高效地执行著名的Shor数字因式分解算法等。”Fellner 说。

实现两级纠错

新概念还提供硬件上的高效纠错。由于量子系统对干扰非常敏感，因此量子计算机必须不断纠正错误。必须投入大量资源来保护量子信息，这大大增加了所需的量子比特数。

“我们的模型采用两级纠错，一种类型的错误（位翻转错误或相位错误）可以通过使用的硬件来防止，”同样是因斯布鲁克研究团队成员的Anette Messinger和Kilian Ender说。他们在不同的平台上已经有了初步的实验方法。

Messinger和Ender说：“其他类型的错误可以通过软件检测和纠正。”这将使下一代通用量子计算机有望通过能商业化的管理和研发实现。目前，由Wolfgang Lechner和Magdalena Hauser共同创立的衍生公司——ParityQC，已经在与因斯布鲁克大学及科学和工业上的伙伴合作，并可能实现新的研究模式。

相关论文可以查阅：Michael Fellner、Anette Messinger、Kilian Ender 和 Wolfgang Lechner 的“通用奇偶校验量子计算”，2022 年 10 月 27 日，物理评论快报。
DOI：10.1103/PhysRevLett.129.180503Michael Fellner、Anette Messinger、Kilian Ender 和 Wolfgang Lechner 的“通用奇偶校验量子计算的应用”，2022 年 10 月 27 日，Physical Review A。
DOI：10.1103/PhysRevA.106.042442

编译：王珩

​编辑：慕一