codeforces807div2 D.Dynamic Problem Scoring[暴力][贪心]

最新推荐文章于 2024-07-24 13:02:49 发布

原创最新推荐文章于 2024-07-24 13:02:49 发布 · 525 阅读

1 ·

CC 4.0 BY-SA版权

思维同时被 2 个专栏收录

8 篇文章

订阅专栏

暴力

1 篇文章

订阅专栏

Vasya and Petya take part in a Codeforces round. The round lasts for two hours and contains five problems.

For this round the dynamic problem scoring is used. If you were lucky not to participate in any Codeforces round with dynamic problem scoring, here is what it means. The maximum point value of the problem depends on the ratio of the number of participants who solved the problem to the total number of round participants. Everyone who made at least one submission is considered to be participating in the round.

$\text{[math]}$

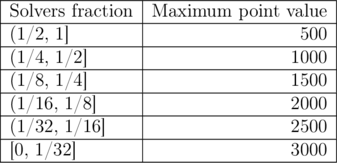
Pay attention to the range bounds. For example, if 40 people are taking part in the round, and 10 of them solve a particular problem, then the solvers fraction is equal to 1 / 4, and the problem's maximum point value is equal to 1500.

If the problem's maximum point value is equal to x, then for each whole minute passed from the beginning of the contest to the moment of the participant's correct submission, the participant loses x / 250 points. For example, if the problem's maximum point value is 2000, and the participant submits a correct solution to it 40 minutes into the round, this participant will be awarded with 2000·(1 - 40 / 250) = 1680points for this problem.

There are n participants in the round, including Vasya and Petya. For each participant and each problem, the number of minutes which passed between the beginning of the contest and the submission of this participant to this problem is known. It's also possible that this participant made no submissions to this problem.

With two seconds until the end of the round, all participants' submissions have passed pretests, and not a single hack attempt has been made. Vasya believes that no more submissions or hack attempts will be made in the remaining two seconds, and every submission will pass the system testing.

Unfortunately, Vasya is a cheater. He has registered 109 + 7 new accounts for the round. Now Vasya can submit any of his solutions from these new accounts in order to change the maximum point values of the problems. Vasya can also submit any wrong solutions to any problems. Note that Vasya can not submit correct solutions to the problems he hasn't solved.

Vasya seeks to score strictly more points than Petya in the current round. Vasya has already prepared the scripts which allow to obfuscate his solutions and submit them into the system from any of the new accounts in just fractions of seconds. However, Vasya doesn't want to make his cheating too obvious, so he wants to achieve his goal while making submissions from the smallest possible number of new accounts.

Find the smallest number of new accounts Vasya needs in order to beat Petya (provided that Vasya's assumptions are correct), or report that Vasya can't achieve his goal.

Input

The first line contains a single integer n (2 ≤ n ≤ 120) — the number of round participants, including Vasya and Petya.

Each of the next n lines contains five integers ai, 1, ai, 2..., ai, 5 ( - 1 ≤ ai, j ≤ 119) — the number of minutes passed between the beginning of the round and the submission of problem j by participant i, or -1 if participant i hasn't solved problem j.

It is guaranteed that each participant has made at least one successful submission.

Vasya is listed as participant number 1, Petya is listed as participant number 2, all the other participants are listed in no particular order.

Output

Output a single integer — the number of new accounts Vasya needs to beat Petya, or -1 if Vasya can't achieve his goal.

Examples

input
2
5 15 40 70 115
50 45 40 30 15

output
2

input
3
55 80 10 -1 -1
15 -1 79 60 -1
42 -1 13 -1 -1

output
3

input
5
119 119 119 119 119
0 0 0 0 -1
20 65 12 73 77
78 112 22 23 11
1 78 60 111 62

output
27

input
4
-1 20 40 77 119
30 10 73 50 107
21 29 -1 64 98
117 65 -1 -1 -1

output
-1

Note

In the first example, Vasya's optimal strategy is to submit the solutions to the last three problems from two new accounts. In this case the first two problems will have the maximum point value of 1000, while the last three problems will have the maximum point value of 500. Vasya's score will be equal to 980 + 940 + 420 + 360 + 270 = 2970 points, while Petya will score just 800 + 820 + 420 + 440 + 470 = 2950 points.

In the second example, Vasya has to make a single unsuccessful submission to any problem from two new accounts, and a single successful submission to the first problem from the third new account. In this case, the maximum point values of the problems will be equal to 500, 1500, 1000, 1500, 3000. Vasya will score 2370 points, while Petya will score just 2294 points.

In the third example, Vasya can achieve his goal by submitting the solutions to the first four problems from 27 new accounts. The maximum point values of the problems will be equal to 500, 500, 500, 500, 2000. Thanks to the high cost of the fifth problem, Vasya will manage to beat Petya who solved the first four problems very quickly, but couldn't solve the fifth one.

题意：两个好朋友参加一场动态计分的比赛，根据比赛要求，每个题的分数与题的正确比率有关，每个人的每个题得分与作出题的时间和题目分数有关。为了让A战胜B，A开了很多小号来提交正确或错误，问最少的提交次数能战胜B。

思路：

一共初始状态最多120人参赛，所以为了让一个题的分数限定在500分或者3000分，只需要大约3000个小号，所以五个题最多需要上万个小号吧，再多了也没有什么作用，所以对使用小号的个数进行暴力即可，针对每个小号如何提交才能达到最优状态，采用贪心的方式：

如果A没有做出来这题，所有小号一定无法正确提交。

如果A做出来了这题，但是B没有做出来，为了使此题分数最大，A的小号都提交错误答案。

如果A做出来了这题，B也做出来了，但是A比B做的快，次情况同上。

如果A做出来了，但B做的比A快，为了使此题分数最小，A的小号都正确提交。

按照以上贪心方式提交，即可判断当前小号个数下五个题的分数谁高，是否满足条件。

（比较坑的一点代码中计算 *(1-x/250)这里精度出错了）

#include<bits/stdc++.h>
using namespace std;
int a[150][150];
int cnt[10];
int n;
int getscore(int id, bool flag, int s)
{
    if(a[flag][id]==-1) return 0;
    int sum;
    if(a[0][id] == -1 || a[1][id] == -1 || a[0][id]<a[1][id]) sum = cnt[id];
    else sum = cnt[id]+s;

    int score = 500;
    for(int i = 2; i <= 32; i*=2)
    {
        if(sum*i > n+s)
            break;
        else score += 500;
    }

    return score*(250.0 - a[flag][id])/250.0;
}


int main()
{
    ios::sync_with_stdio(false);
    cin >> n;
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < 5; ++j)
    {
        cin >> a[i][j];
        if(a[i][j] != -1)
            cnt[j]++;
    }
    //cout << getscore(4, 0, 2);
    for(int i = 0; i < 50000; ++i)
    {
        int a1=0, a2=0;
        for(int j = 0; j < 5; ++j)
            a1 += getscore(j, 0, i);
        for(int j = 0; j < 5; ++j)
            a2 += getscore(j, 1, i);
        //cout << a1 <<" " <<  a2 << endl;
        if(a1 > a2)
        {
            cout << i << endl;
            return 0;
        }
    }
    cout << "-1" <<endl;
    return 0;
}