题意
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N 和 M。
第二行包含一个长度为 N 的字符串,表示字符串 A。
第三行包含一个长度为 M 的字符串,表示字符串 B。
字符串均由小写字母构成。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N,M≤1000
输入样例:
4 5
acbd
abedc
输出样例:
3分析
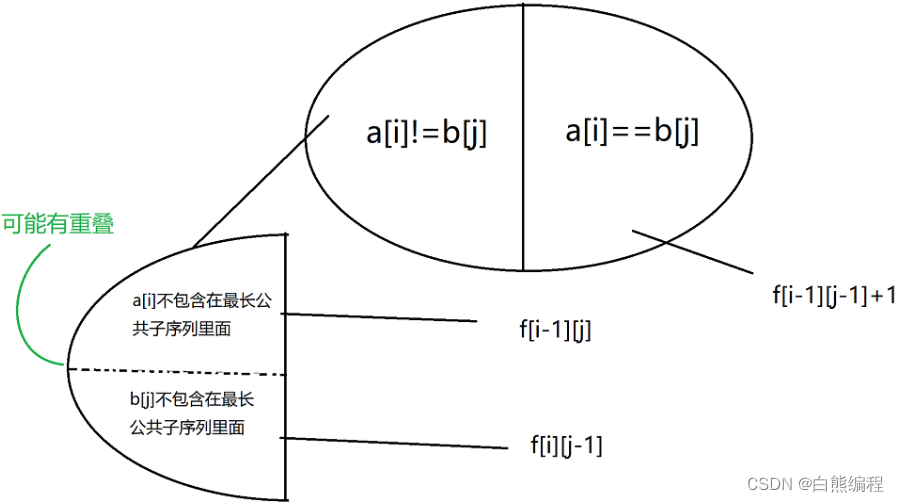
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
char a[N],b[N];
int dp[N][N];
int n, m;
int main() {
cin >>n>>m;
cin>>a+1>>b+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
if(a[i]==b[j])
dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
}
}
cout<<dp[n][m];
return 0;
}



























 442
442

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








