嵌入式面试题(6)：智力题

最新推荐文章于 2021-01-24 19:04:37 发布

「已注销」

最新推荐文章于 2021-01-24 19:04:37 发布

阅读量955

点赞数

分类专栏：面试

本文链接：https://blog.youkuaiyun.com/QQ2558030393/article/details/89358875

版权

面试专栏收录该内容

12 篇文章

订阅专栏

这篇博客主要包含一系列的智力题，涉及数学推理、逻辑思维和实际问题解决。例如，通过立方数推理找到特定数值，青蛙爬井问题，找出数组中的重复数字，利用天平找出不同重量的球等。这些问题展现了在嵌入式领域面试中可能遇到的思维挑战。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

提问:已知11的立方等于1331,12的立方等于1728,那么什么数的立方等于1442897

推论：1442897应该是一个整数的立方,它给你11立方和12的立方一定会用到.1442897是个7位数,100的立方是1000000也是7位数.200的立方是8000000也是7位数.则1442897应该是100-200间的一个数.
110的立方是1331000（加3个0）120的立方是1728000,1442897在其范围内,则应该是110-120间的一个数,也就是说应该是111-119（确定个位数）
又因为
是1
是8,27,64,125,216,343,512,729……（得数的尾数都不相同,且占满1-9）也就是说确定尾数就能知道它是几的立方数
结果尾数是7,对应的数字是3,则个位数是3.
则这个数就是113

一只青蛙掉进一口18英尺深的井。每天白天它向上爬6英尺，晚上向下滑落3英尺。按照这一速度，多少天它能爬出井口?

晚上的时候青蛙才会往下滑,由于白天正好是晚上的两倍,设要x白天y个黑夜青蛙能爬上井口
那x=y或x=y+1,x=y可以不用考虑,因为当经过一晚下滑还在井上的话,那肯定在白天就已经爬出了
6x-3y>=18
6x-3(x-1)>=18
x>=5
则5天后青蛙爬处井口

100大小的数组放了1-99 100个数，只有一个数重复了，找出重复的那个数。

答:解法很简单，把这100个数加起来，然后逐一剪掉1-99 剩下的那个数就是重复的数。

101个硬币100真、1假，真假区别在于重量。请用无砝码天平称两次给出真币重还是假币重的结论。

101个先取出2堆,
33,33
第一次称,如果不相等,说明有一堆重或轻那么把重的那堆拿下来,再放另外35个中的33
如果相等,说明假的重,如果不相等,新放上去的还是重的话,说明假的轻(不可能新放上去的轻)
第一次称,如果相等的话，这66个肯定都是真的,从这66个中取出35个来,与剩下的没称过的35个比

做这种题就是开始平均分成3堆，然后再比较

1,3, 5, 9, 17, 31, 57,

两个数之间的差值是前两个数的和。

某专业有50名学生，开设有甲、乙、丙三门选修课。有40人选修甲课程，36人选修乙课程，30人选修丙课程，

兼选甲、乙两门课程的有28人，
兼选甲、丙两门课程的有26人，
兼选乙、丙两门课程的有24人，
甲、乙、丙三门课程均选的有20人。
问三门课程均未选的有多少人？（）

第一种：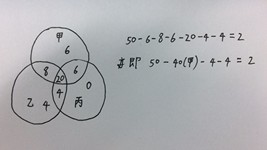

第二种：最简单

40+36+30-28-26-24+20=48

50-48=2

有9个球,其中一个的质量与其他的不同,有一个天平,通过最多几次可以找出那个质量不一样的球?

任取2组比较，若重量相等，则目标小球在另一组；

若重量不等，则任意替换一组再进行比较，可以知晓目标小球所在组，以及目标小球重量比一般小球是重还是轻（这点很关键）。

对目标小球所在小组任取2个，若重量相等，则目标小球为另一个；若重量不等则可以根据之前获取的目标小球重量特征（比一般重或轻），找出目标小球。

共称3次。

推理题

一看到左边就要想到右边

65 = 8^2+1
8  = 3^2-1
50 = 7^2+1
15 = 4^2-1 
37 = 6^2+1 
24 = 5^2-1

有2分盐，一份120克，一份10克，用一个天平最少几次可以称出一份25克的盐？

第1次：120平分，得到60

第2次：60平分，得到30

第3次：30平分，得到15，和剩下的10加在一块就是25

推理数的问题总结

当前项等于前两项之和 / 2 如：4,12,8,10,(9)
分数值全是相等的如：133/57,119/51,91/39,49/21,(28/12),7/3

天平问题的模板

有n个球，其中1个球是次品，质量比其他球都要重（或要轻）。现在有一个没有砝码的天平，要求称t次，将次品球挑出。

当 $3^{t} > = N$ 时，有解

有n个球，其中1个球是次品，质量与其它球不同。现在有一个没有砝码的天平，要求称t次，将次品球挑出。

则当 $3^{t} >= 2N$ 时，有解，且当且仅当 $3^{t} = 2N + 1$ 时，需要1个标准球辅助。

量子力学：物理学：化学，正确选项为（）

颜色：黑：白
步兵：陆军：空军
医院：医生：护士
哲学：文学：美学

量子力学属于物理学，而物理学和化学是平行学科
步兵属于陆军，而陆军和空军是平行的

约瑟夫环问题

取奇数问题

500 张纸牌整齐排成一排，按顺序编号 1、2、3、4、...、499、500，第一次拿走所有奇数位置上的纸牌，第二次再拿走剩下纸牌中的所有奇数位置上的纸牌，以此类推操作下去，问最后剩下的纸牌的编号是多少 ?

和上面循环取数不同，上面有循环的规律（头尾相接），而这个没有循环的规律

第一次剩下是2的倍数第二次剩下的是4的倍数最后剩下128和256 拿走128 剩下256

简单例举下：0 1 2 3 4 5 6 7 8 9 10 11

第一次剩下的 1 3 5 7 9 11 规律： 2i-1

（ i为整数 1<=i<= n/2 （n表示给出序列的元素个数，例子中是12，而题目中是501））

第二次剩下的 3 7 11 4i- 1 1<=i<= n/4

第3次剩下的 7 8i- 1 1<=i<= n/8

计算50的阶乘，结果末尾处有多少个0？

50！末尾0的个数，即求50！中 2X5 的因子的个数，有多少个 2X5 的因子，就有多少个0

由于 2 的因子个数远大于 5 的个数，所以转换为求 5 的因子个数

1~50中，有5 10 15 20 25(5X5) 30 35 40 45 50(5X5X2)，注意黑体的有两个5，总共12个

图形推理题=====================================

答案在下一题------------------------------------------------------------------------------------------------------------------------------------------------

选D：因为保证每行每列都有两个重复的图形。

答案在下一题------------------------------------------------------------------------------------------------------------------------------------------------

题目中，每一个图形都由两部分组成，中间一个大圆，周围有若干小圆。而大圆又分为两种颜色，一种白色，一种黑色。

白色大圆带着的小圆的权重是1，黑色大圆带着的小圆权重是3，而每一行的第三个图形，都是由前两个图形叠加得到。

这样一来，

第一行构成等式：

1X3 + 3X3 = 3X4

第二行构成等式：

3X2 + 1X4 = 1X10

第三行构成等式：

1X1 + 3X2 = ？

问号处，显然是 1X7。所以答案是D：

答案在下一题------------------------------------------------------------------------------------------------------------------------------------------------

下面的？是什么

每一行是3个不同形状图形,每一行都有一个黑色的小圆,两个白色小圆，且每行各类小圆在图形外1个,在图形里2

答案在下一题------------------------------------------------------------------------------------------------------------------------------------------------

每行的前三个之和除以3为第三个的值

答案在下一题------------------------------------------------------------------------------------------------------------------------------------------------