基于MATLAB的雾天图像清晰化研究

摘 要

图像是人们认识和感知世界的重要媒介，随着计算机视觉和数字图像处理领域的迅猛发展，各种基于图像的智
能检测系统逐渐渗透进我们的生活。然而各种图像采集设备常常会受到恶劣天气的干扰，使获取到的图像对比度
低，细节缺失，色调失真，导致依赖图像工作的智能系统难以保持正常运行。因此进行雾天图像清晰化研究对人类
社会的进步具有深远影响。
　　本文对雾天图像清晰化算法进行了深层次的研究，利用MATLAB平台改进直方图均衡化、Retinex理论、暗通道先
验这三类图像清晰化算法并最终将其实现，最后基于GUI设计了雾天图像清晰化系统。
本文主要工作如下：
　　（1）在基于直方图均衡化的图像增强去雾算法方面，研究并总结全局直方图均衡化和限制对比度自适应直方图
均衡化，并从主观评价指标和客观评价指标两方面对效果做出评定。
　　（2）在基于Retinex理论的图像增强去雾算法方面，详细阐述Retinex算法的基本原理、算法分类、实验步骤，
重点研究单尺度Retinex（SSR）算法和多尺度Retinex（MSR）算法。实验结果显示，该方法去雾效果较好，但难以
保持细节和色调间的平衡。
　　（3）在基于暗通道先验的图像复原去雾算法方面，对暗通道先验的原理及算法处理步骤进行分析。由于软抠图
实时性较差，本文使用引导滤波算法对透射率进行优化估计。针对暗通道处理后图像过暗，提出用自动色阶算法调
整颜色。经过实验分析，改进算法复原图像效果较好，实时性强。
　　（4）在本文的研究基础上，基于GUI设计了雾天图像清晰化系统，包括去雾算法效果对比、客观评价指标对
比、直方图对比三个模块，使去雾算法效果对比更加直观。
关键字：雾天图像清晰化；直方图均衡化；Retinex理论；暗通道先验

1 绪论

1.1 研究背景和意义
　　图像是人类利用光学采集设备所获取的外界景物的客观映射，是人类感知和认识世界的首要途径，也是传递和
交换信息的重要媒介。随着计算机视觉与图像处理研究的深入发展，各种依赖图像工作的智能系统广泛应用于生活
的方方面面，例如交通监控、卫星遥感、自动驾驶、军事侦察等领域，而图像的质量对智能系统中物体的识别和检
测、运动与追踪具有重要影响。
　　在实际应用中，传感装置往往会受到诸多因素的影响，例如成像设备本身质量问题、设备持握不稳导致与拍摄
景物产生错位运动，以及恶劣天气状况下图像可视化程度降低等情况，这些不利因素会使拍摄图像产生程度不同的
退化，影响图像本身视觉效果，导致智能系统难以正常工作。随着科技水平的提高，成像设备制作工艺越来越精
良，人为因素引起图像退化的概率逐渐变小，恶劣天气因素逐渐占据主导地位，而雾天又是恶劣天气状况中最常见
的一种形式，由此可见，雾天图像清晰化研究具有重要的现实意义。
　　随着气温升高，在空气湿度足够大的情况下，若近地面水汽含量达到饱和的程度，那么多余的水汽便会相互依
附，从而凝结构成细微悬浮水滴，形成了雾。雾本身没有任何危害，却被视为一种自然灾害，原因是雾天空气能见
度下降，使视觉成像系统采集的图像退化，给许多依赖图像工作的智能系统带来很大限制，给人类生产生活徒增很
多困难。
　　成像设备采集到的光线是物体反射的太阳光，晴天场景下，空气中悬浮着很多水汽、杂质，但这些微小颗粒直
径过小，不会对物体反射光的传播产生很大影响；而在雾天场景下，空气中凝结的大量悬浮水滴会对物体反射光和
大气环境光产生散射作用。散射现象改变了光线在空气中的传播进程，使物体反射光能量在被成像系统捕捉前就大
大削弱，因而成像设备无法接收到物体真实反射光。与此同时环境光也混杂在成像中，造成图像对比度饱和度大幅
下降、细节模糊、物体特征不明确等问题，严重时会使图像保真度大大降低，难以反映物体真实信息。

图1.1 户外雾天图像
　　图1.1是在雾天场景下采集到的图像，可以观察到两幅图像的对比度明显降低，细节部分模糊，颜色较为暗淡，
视觉效果很差。因此深入研究雾天图像去雾方法，提高图像质量，还原物体细节和信息，进而能够优化各种检测、
遥感户外成像系统，增强系统自适应性、可靠度与利用价值，更好地为人类的生产生活服务。
1.2 国内外研究现状

图像去雾是指通过技术手段对雾天降质图像进行处理，增强图像对比度和清晰度，使人眼能获得更佳的视觉效
果，同时智能检测系统能获得更精确的结果。目前雾天图像清晰化算法可以分为两大类，如图1.2所示，基于图像增
强的方法[1-14]和基于图像复原的方法[15-25]。
图1.2 图像去雾算法分类
1.2.1 基于图像增强的雾天图像清晰化算法
　　图像增强是不借助物理模型，不计及雾天图像退化的本质原因，仅依靠算法使图像对比度增大的去雾算法。该
类方法让雾气中悬浮水滴的影响最小化，弱化雾气影响并非从图像中去除雾气。该方法的优势在于可以应用现有成
熟的图像处理算法，常见的图像增强算法有直方图均衡化[1-3]、小波变换[4-5]、同态滤波[6-7]、Retinex理论[8-
14]等。
（1）直方图均衡化
　　雾天降质图像具有对比度低，颜色暗淡，灰度值过于集中的特点。直方图均衡化是指对原始图像的灰度直方图
分布范围进行线性拉伸，增加量化间隔来增大反差，获得更好视觉效果。
　　常见的直方图均衡化有全局直方图均衡化和局部直方图均衡化。前者是将彩色图像三通道分离，分别进行全局
直方图均衡，不可避免地导致大量灰度级数合并，致使图像局部细节丢失，边缘模糊；后者利用模板对像素点进行
邻域操作，首先将图像分块处理，对各个子块进行直方图均衡，将子块中心值作为该像素点均衡化后的值，通过平
移遍历每一个子块，可见该方法计算量巨大，耗时很长。为解决计算量大的问题，Kim等[1]提出了采用非重叠子块
的直方图均衡化算法，在局部直方图均衡化的基础上，增添了非重叠子块模块、双线性插值模块、限制对比度模
块，能够有效降低算法计算量，并抑制块状效应的产生。李竹林[2]等基于直方图均衡化提出了自适应雾天图像清晰
化算法，转换到HIS空间，分别对亮度分量和饱和度分量做自适应直方图均衡化。毕秀丽[3]等利用直方图和累积分
布函数，从而提取出痕迹特征，使用K最临近算法对特征进行分类。
（2）小波变换
　　小波变换能使图像被分解成低频分量和高频分量。低频分量体现平滑区域的主要特征，又称近似分量；高频分
量体现边缘纹理等细节特征，又称细节分量。采用不同方法对两分量实现去噪增强，再进行小波重构，还原清晰图
像。
　　基于小波变换的方法能够提升图像对比度，但很难在增强图像细节和抑制住噪声间保持平衡。SE等[4]采用对比
度熵增强小波变换后的高频分量，采用直方图均衡化增强小波变换后的低频分量。贺欢[5]等利用YCbCr颜色空间对Y
分量进行小波变换，分别处理高低频分量，同时结合RGB颜色空间的均衡图像进行线性组合。
（3）同态滤波
　　同态滤波是指在频率域处理图像，依据照度反射模型，结合灰度变换方法，把图像分解为反射率和照度两个分
量。反射率分量改变较快作为高频分量，而照度分量改变较慢作为低频分量，分别处理再进行反变换，从而改善照

度不均的情况。董静薇等[6]使用小波变换替代了传统同态滤波算法中的傅里叶变换，达到增强对比度，突出轮廓细
节的目的。李开伟等[7]依据同态滤波设计滤波函数，抑制图像低频分量，增强高频分量，进而提升图像质量。
（4）Retinex理论
　　Retinex理论即人类视觉彩色恒常性理论，又称为视网膜大脑皮层理论，是由视网膜retina和大脑皮层cortex的
缩写构成的，最早由Edwin Land等人[8-9]提出，指出一幅图像可由反射分量R和照射分量L的乘积表示。物体的本质
特性由反射分量体现，大气光照的影响由照射分量体现。计算步骤如下，首先将图像进行颜色通道分解，再转换到
对数域进行后续操作。反映大气光影响的照射分量L是利用高斯滤波器和原始降质图像的卷积得到的，体现物体固有
特性的反射分量R是将照射分量L从原始降质图像减去得到的。最后做指数运算，恢复出清晰无雾图像。
　　Jobson等人[10]在Retinex理论的基础上引入了高斯函数进行滤波，被称为単尺度Retinex（SSR）算法，后续又
提出了多尺度Retinex(MSR)算法[11]，即使用不同尺度的SSR算法再加权组合，综合不同尺度的优势。带颜色恢复的
多尺度Retinex算法[12]在MSR的基础上增设了颜色恢复因子，记录三通道的原始颜色比例，解决颜色失真问题，但
该算法效率低下。国内也有许多学者在Retinex理论基础上进行改进，如李武劲[13]等将图像转换到HSV空间，针对
亮度分量采用大气散射模型和改进的基于双边滤波的Retinex算法进行去雾，并对饱和度进行指数调整，再转换回
RGB空间。魏然然[14]等使用引导滤波替代传统高斯滤波对反射分量进行估计，用较为平缓的非线性曲线进一步校
正，最后对入射分量做自适应灰度拉伸处理。
1.2.2 基于图像复原的雾天图像清晰化算法
　　基于图像复原的方法考虑到降质图像退化的根本原因，研究悬浮在空气中的微粒对光的散射来建立大气散射模
型，即成像包含了物体反射光和大气环境光的共同作用，求解模型当中的参数来复原无雾图像。和图像增强的算法
相比，利用了图像更多信息，整体去雾效果更为真实自然。常见的图像复原算法有基于大气光偏振特性的算法[15-
16]、基于场景深度的算法[17-19]、基于先验信息的算法[20-25]等。
（1）基于大气光偏振特性的算法
　　基于大气光偏振特性的方法认为物体反射光为非偏振光，而经过散射的大气环境光为部分偏振光。根据同一场
景多幅偏振图像可以估算出大气散射光，再从降质图像减去大气环境光获取物体真实反射光。该类算法利用更多图
像信息，能够在雾天图像去雾上达到较好的效果，但是实际应用不一定提供同一景物多幅图像，况且仅在薄雾天气
下，光的偏振特性才明显，给该类方法带来了很大的局限性。夏宏丽[15]等根据暗通道先验理论计算大气光值和景
深，然后利用场景深度信息求解偏振度值，最后复原得到图像的辐射强度信息。周浦城[16]等基于偏振图像暗通
道，自动提取大气光强，基于归一化互信息的原则优化偏振度，改善大气光强分布后作为加性噪声从图像中去除，
该方法有效改善了图像清晰化程度。
（2）基于场景深度的算法
　　根据大气散射模型可以得出，透射率的大小与景物深度呈指数关系，成像装置距离被拍摄物体越远，图像越模
糊，雾气越浓厚；成像装置距离被拍摄物体越近，图像越清晰，雾气越稀薄。利用这一特征，通过其他手段获取场
景的透射率，便可求得大气散射模型的其他参数值，进一步反演出退化前的真实图像。例如借助雷达获取图像信
息、根据多幅图片进行场景三维重构等。该类方法需要借助附加手段，或者提供多幅图像才能实现，无法应用到单
幅图像的清晰化研究中，因而在现实生活中没有得到广泛应用。
　　最早由Oakley等[17]使用先进探测设备获得场景深度，提出简单算法估计光路参数，处理后图像视觉效果好，
但该方法事前测量需耗费大量人力物力财力，推广难度大。Nayar等[18]利用不同天气状况下的场景图像，对该场景
进行三维重构，估计场景深度信息，同时利用大气散射模型对雾天降质图像进行复原。Narasimhan等[19]通过用户
截取天空区域并输入景深范围，粗略估计场景深度，结合大气散射模型进行去雾，该算法需要人机交互，受人为因
素影响较大，实时性差。
（3）基于先验信息的算法
　　近年来基于先验信息的算法得到了业界很多关注，发展迅猛且去雾效果良好。在拥有一定假设条件或先验信息
的前提下，得出图像的某一重要信息，例如大气光值、透射率等，进而通过大气散射模型得到其他参数，反演出降
质前无雾图像。如Tan等[20]借助最大化图像局部对比度的方法对雾天降质图像进行处理，去雾后图像对比度大幅提
升，但容易产生颜色过饱和问题。Tarel等[21]针对公路场景，利用中值滤波对大气耗散函数进行粗略估计，再经过
色调调和对图像进行复原，但在景物边缘容易产生光晕效应。Fattal[22]基于数据统计理论，假设场景的阴影部分
和光线传播是不相关的，从而估计出图片反射分量和透射率，但无法应用于浓雾或过于灰暗缺乏细节信息的图像。
　　2009年，He等[23]创造性地提出了一种基于暗原色先验的去雾算法，在经过观测大量户外雾天图像后总结出暗

通道这一理论，以此作为图像的先验信息计算出图像的暗通道，进而计算大气光值和图像透射率，再根据大气散射
模型得到去雾后的清晰图像，去雾效果真实，简单有效。HE等为了进一步优化透射率估计，采用软抠图方法，但大
量稀疏矩阵运算复杂，计算量大，耗时过长。为了解决实时性差的问题，HE等提出用导引滤波代替软抠图算法，大
大缩短了运行时间，但在处理图像天空区域或其他白色区域时，仍会出现不同程度的色彩失真问题。
　　暗通道先验理论去雾效果好，引起了许多研究人员关注，如马啸[24]等基于暗通道先验理论，将算法中区域大
小固定不变调整为随图像大小而变化，同时增设大气光强阈值，采用引导滤波代替软抠图算法。MENG等[25]提出了
基于加权范数的边界约束方法，并结合边界正则化优化透射率，虽然保留更多细节信息，但部分区域仍存在颜色失
真的情况。
1.3本文研究重点
　　本文在广泛阅读国内外文献的基础上，通过MATLAB软件开展雾天图像清晰化研究。本文主要采用基于直方图均
衡化、Retinex理论、暗通道先验理论的相关算法，实现了雾天降质图像的清晰化处理，并综合主客观评价指标对图
像质量加以评定。本文实现及改进的算法去雾效果较好，恢复后图像对比度高，细节特征明显。此外，基于GUI制作
了雾天图像清晰化系统，能够实时展示去雾效果和评价指标结果。
1.4论文组织结构
本文主要分为七章，各章节内容安排如下：
　　第一章，绪论。本章在广泛阅读文献的基础上总结了去雾算法的背景意义和该领域研究现状，并且阐述了研究
重点内容和论文组织结构。
　　第二章，图像去雾基础理论。本章首先简要分析了雾天成因，介绍了雾天图像退化特征，然后分析了大气散射
物理模型的主要构成，最后详细说明了去雾图像的评价方法。本章为后续章节雾天图像清晰化算法提供重要的理论
基础。
　　第三章，基于直方图均衡化的雾天图像清晰化研究。首先对直方图均衡化的原理进行介绍，接着运用全局直方
图均衡化和限制对比度直方图均衡化两种方法进行对比性实验分析，最后依据主客观评价指标判定去雾效果。
　　　　第四章，基于Retinex理论的雾天图像清晰化研究。首先阐明了基本原理与算法分类，接着重点研究了単尺
度Retinex（SSR）算法的原理与步骤。然后尝试使用多尺度Retinex（MSR）算法，对大中小三个尺度的SSR算法进行
加权融合。最后通过图像集衡量算法的去雾效果。
　　　　第五章，基于暗通道先验的雾天图像清晰化研究。首先细致地分析了该类方法的基本原理和实现步骤。针
对软抠图算法优化时计算时间过长的问题，使用引导滤波算法对透射率进行改善。针对暗通道处理后图像过暗的问
题，本文提出用自动色阶算法调整颜色。最后对各种方法的效果进行分析。
　　第六章，基于GUI的雾天图像清晰化系统设计。首先介绍了MATLAB图形用户界面，然后简要介绍了雾天图像清晰
化系统的界面设计和软件设计，最后分析展示了去雾系统运行效果。
　　第七章，总结与展望。回顾了本文完成的主要工作，并且指明了本文算法值得改进的方向。

2 图像去雾基础理论

雾天图像细节模糊，颜色泛白，对比度低，非常不利于基于图像的智能系统正常运行。雾天图像清晰化技术涵
盖数学，物理学等多学科多领域的知识，因此为了更好地对雾天图像进行处理，本章将对雾天形成原因、雾天降质
图像特征、大气物理散射模型、图像质量评价指标等进行重点研究。
2.1 雾天成因与降质图像特征
2.1.1 雾天形成原因
　　雾天是一种常见的天气形式，由近地面空气中无数悬浮水滴和冰晶构成。雾的形成机理需要满足以下三个条
件，一是空气温度较低，二是空气中水汽含量足够高，三是风力不够强，空气中的悬浮颗粒无法快速扩散开。空气
温度越低，则水汽饱和阈值越小，越容易凝结成小水珠，这是因为只有当空气中的水汽含量大于特定温度下的饱和
阈值时，多余的水蒸气才会相互粘连从而形成小水滴，大量的小水滴悬浮于空气中就形成了雾。生活中比较常见的
两种情况是潮湿空气慢慢冷却下来，或是暖空气流遇到低温地面，最终形成了雾。
2.1.2 雾天降质图像特征
　　雾能够散射大部分可见光，云也能够散射大部分可见光，因此人眼观察到的雾通常像云一样呈白色。雾也可以
视为噪声，对远处景物起遮挡作用，大大降低空气能见度。由于能见度低下，不仅人眼看上去灰蒙蒙一片，户外成
像设备采集到的图片也具有对比度低下，颜色单一，色调单薄，物体细节特征消失等特点，不利于后续处理。图片
细节模糊程度和雾的大小呈正相关，根据能见度大小，可以将雾划分为轻雾和浓雾。由此可见，研究雾天图像清晰

化对人们的生产生活都有很大作用。
　　物体的反射光线穿过雾气时，会和悬浮水滴发生作用产生额外散射，沿着主要路径的反射光线能量逐渐衰减，
严重降低了光线传播的透射率，致使成像设备接收到的物体反射光是不完整的。其余大气环境光经过散射参与成
像，叠加在物体反射光上，从而增加了图像亮度，打破了彩色RGB三通道间的平衡，导致图像色彩偏移，严重时出现
色彩失真的情况。此外还会引起图像像素动态范围压缩，使雾天降质图像灰度级分布更加集中，动态范围压缩程度
随着雾的大小而变化，雾越大动态范围越窄，颜色层次越少，涵盖图像信息越少。
2.2 大气散射物理模型
　　在雾天图像清晰化算法分类中，图像增强的方法不借助任何物理模型，仅通过施加不同图像处理手段使图像的
饱和度得到增加，对比度得到增强，图像细节机理更加突出，但却忽略了雾天图像质量下降的本质原因。相反，图
像复原的方法是基于大气散射模型对图像进行处理，分析了真实物理过程，因此能够真正实现去雾的目的。此类方
法往往通过大气光偏振特性、场景深度信息、先验信息等得到大气散射模型中的参数，从而反演出清晰图像。
　　大气散射模型最早是由McCartney提出的物理模型，探究了光线和空气悬浮微粒的相互作用，在传播过程中会发
生辐射，吸收和散射作用，辐射和吸收两种类型损耗的光能较小，散射作用才是导致物体反射光到达成像设备前产
生衰减的主要因素。大气散射过程较为复杂，照射到景物的入射光会经历散射，被成像设备捕获的景物反射光也会
经历散射。因此从物理角度分析可以将大气中光线的散射分为两部分，一部分是成像设备的入射光即景物反射光在
传播过程中的散射；另一部分是其余大气环境光的散射，叠加在雾天反射光上，影响成像效果，相当于附加成像光
源。当景深较小时，影响成像的主要是反射光衰减模型，当景深较大，距离景物较远，大气光及环境光才是影响成
像的主要因素。大气散射物理模型示意图如图2.1所示。

图2.1 大气散射物理模型示意图
2.2.1 入射光衰减模型
　　该模型说明了目标物体的反射光线在主要传播路径上，遇到雾气中的悬浮水滴会发生散射现象，使反射光线强
度逐渐衰减，并且能量衰减的程度和景深呈正相关，入射光衰减模型的示意图如图2.2所示。

图2.2 入射光衰减模型示意图

首先假设空气中悬浮微粒是均匀分布的，如图2.3所示，物体反射光经过长度为dx的含雾空气薄片后，光强衰减
量
可以表示为：
（2.1）
　　式（2.1）中，
是传播距离 处入射光的光照强度， 是光线波长，
表示衰减后入射光光照强
度，
是大气散射系数，对上式左右两端在x属于[0,d]范围内积分，可以写为：
（2.2）
（2.3）
进一步化简得到入射光在景深为d处的光照强度：
式中，
为物体反射光的原始光照强度，
为成像设备接收到的光照强度。
2.2.2 大气光成像模型
　　在设备成像时，物体反射光经历衰减后进入成像系统。除此以外，大气环境光也会进入成像系统，从而带来附
加影响，且该不利影响和景深呈正相关。通常将未经散射的太阳光、经过散射的其他物体反射光、来自地面的反射
光等都归类为大气环境光。大气光成像模型的示意图如图2.4所示。

图2.4大气光成像示意图
图2.5大气光成像模型

射率，即原始清晰图像经历散射成功到达图像采集设备的几率。
　　基于物理模型的图像复原过程，就是根据
恢复
的过程。学者通常根据先验信息，计算得到大气光值和
透射率，进一步求出复原后的图像。大气散射模型是研究雾天图像清晰化的理论依据。
2.3 图像质量评价指标
　　雾天图像清晰化处理需要评价指标对恢复后的清晰图像进行有效评价，当前在图像处理领域，没有统一的标准
进行评判，通常采取主客观评价指标相结合的方式。
2.3.1 主观评价指标
　　主观评价指标是从人的视觉感受出发，由人为因素主导的一种评价方式。图像处理结果可以划分为不同等级，

去雾图像质量非常高，人眼视觉效果非常满意
去雾图像质量较好，人眼视觉效果较为满意
去雾图像质量一般，人眼视觉效果一般
去雾图像质量较差，人眼视觉效果较不满意
去雾图像质量极差，人眼视觉效果非常不满意
一般
差
非常差
　　主观评价结果会收到很多因素干扰，很多时候判断不严谨，况且该方法需要投入大量人力物力进行反复实验。
同一个人在不同光线效果，不同时间下对同一图片的判断都会有偏差。其他干扰因素，例如评审员个人喜好、是否
具备专业知识、个人审美、个人情绪等等，都会严重影响到主观评价实验的参考价值。为了更科学地对处理结果进
行评定，就需要采用客观评价指标来进一步分析。
2.3.2 客观评价指标
　　客观评价指标是指用数学公式的结果度量图像质量，计算图像特定属性参数进行对比，将图像的特征值转化为
指标，具有数据直观，计算简便的特点。根据是否需要景物晴朗天气下的无雾图像，可以将客观评价指标划分为无
参考评价和有参考评价。前者不需要被拍摄对象在无雾天气下的照片作为参照，仅根据复原后图像自身属性进行计
算，常用的指标有标准差、信息熵、平均梯度、对比度等；后者需要参照被拍摄对象在晴朗天气下的清晰图像，这
一条件在实际应用中很难被满足，所以其应用往往受到很大限制，常见的方法例如结构相似性，峰值信噪比等。
本文选取亮度均值、标准差、信息熵、结构相似性、峰值信噪比这五种客观评价指标，以此判定图像的去雾效果。
（1）亮度均值
亮度均值指图像各点的平均像素值，公式如下：
（2.13）
　　式中
表示各点像素值， 为图像长度宽度占有的像素个数。亮度均值数值越大表明图像越亮，但图像质
量不一定高，还需要综合其他指标进行判断。
（2）标准差
标准差能够体现各点像素值大小较均值而言分布的离散程度，如式（2.14）所示：
（2.14）
　　式中， 表示亮度均值。标准差数值越大，表示像素灰度的动态范围越广泛，色彩更加丰富饱满；数值越小，表

示图像灰度级分布范围较窄，图像色彩暗淡，细节单一。
（3）信息熵
　　图像的信息量可以由信息熵度量，通常当图像承载更多的信息量时，该数值越大，边缘细节更明显，图像效果
更好，公式如下：
（2.15）
　　其中， 表示灰度级范围，通常为[0,255]， 表示图像中的灰度等级，
表示一幅图像中灰度值为 的像素个
数占总像素个数的比重，信息熵 越大，信息量越大，图像质感越清晰。
（4）结构相似性
　　表示去雾前后两幅图像在结构信息方面的相似程度，通常从亮度、对比度、结构这三个角度来对图像进行分
析，亮度比较函数、对比度比较函数、结构比较函数分别为：
（2.16）
（2.17）
（2.18）
　　其中
为去雾前后图像像素点的亮度均值；
为去雾前后图像像素点的方差，
为常数，结构相似
（2.19）
性（SSIM）计算公式如下：
　　式中，
为取值[0,1]的调整参数。SSIM数值范围为[0,1]，去雾前后图像结构相似程度越高，数值越接近1。
（5）峰值信噪比
峰值信噪比用于比较降质图像处理前后各像素点的误差，公式如下：
（2.20）
式中，
为两幅图像，尺寸大小为M×N。PSNR数值越大，表明图像去雾效果越好，质量越高。
2.4 本章小结
　　本章介绍了图像去雾技术的相关基础理论，首先解释了雾天现象的形成原因，并细致地分析了雾天降质图像的
具体特征。然后从物理学的角度推导了入射光衰减模型以及大气光成像模型的数学公式，进而构成大气散射物理模
型。最后对评判去雾效果时使用的评价指标进行介绍，包括主观评价指标和客观评价指标。本章内容为后续章节提
出的去雾算法提供较为详细的理论基础。

3 基于直方图均衡化的雾天图像清晰化研究

在数字图像处理中，从对图像进行初步分析直至提出行之有效的处理方法都离不开直方图。本章主要研究基于
直方图均衡化的雾天图像清晰化算法，属于基于非物理模型的图像增强类去雾算法。本章采用全局直方图均衡化和
限制对比度直方图均衡化方法进行去雾，并对两者的优势与不足作出总结和分析。

3.1 全局直方图均衡化
　　直方图均衡化算法通过将图像原始灰度分布映射地更加均匀，来增加量化间隔并扩展灰度动态范围。像素灰度
值的数量在直方图均衡化算法中不会被更改，但是会根据出现次数改变相对应的灰度级。因此，相同长度的像素间
隔显示的像素数量大致相等，从而使图像的原始结构不被损坏。
　　本节重点研究全局直方图均衡化，显而易见是对图像进行整体操作，无需分割成多个子块进行处理，将归一化
的直方图表示成：
（3.1）
式中， 为输入图像的所有灰度级； 为灰度级 的像素数目； 为图像像素的总数； 为像素灰度级总数。
进行直方图均衡化对应的离散形式如下：
（3.2）
式中， 为变换函数，表示输入图像的灰度级累积分布函数。
该算法的实现步骤如下：
（1）计算得到原始输入图像的灰度级总数 ，计算灰度级
。
（2）计算原始图像的直方图
（3）计算各灰度级的变换函数
（4）确定新的 到 映射关系。
，即各级灰度值出现的概率。
并进行舍入处理。
（5）计算每个灰度级 对应的像素数目，得到最终结果。
　　MATLAB中提供了histeq函数用于实现图像的均衡化操作，但是输入必须是灰度图像或者二值图像。因此必须将
彩色图像分解为RGB三通道，分别进行处理，最后组合成三维图像。具体代码如下：
1.function In=histequal(I)
2.%分解为RGB三个分量 做全局直方图均衡
3.R = I(:,:,1);G = I(:,:,2);B = I(:,:,3);
4.M = histeq®;N = histeq(G);L = histeq(B);
5.In = cat(3, M, N, L);
6.end
3.2 限制对比度自适应直方图均衡化
　　全局直方图均衡化（HE）是对整个图像的灰度进行拉伸变换，而不考虑各区域内的灰度值变化。全局直方图均
衡化在图像灰度变化范围不大时，增强效果较好，假若图像中存在明显的亮暗区域时，会导致过分增强，色彩失真
等现象。
　　自适应直方图均衡化（AHE）计算图像局部直方图，在矩形小窗口内进行局部均衡化，再遍历全局，继而实现整
个图像的均衡化操作。但是AHE也具有缺点，若窗口内各像素点灰度值接近，直方图在一段区域内具有峰值，经过拉
伸后反而会过度放大噪声，影响去雾后图像质量。
　　限制对比度自适应直方图均衡化（CLAHE）采用直方图规定化处理各个邻域内的像素点。为了消去人工引入的边
界，利用双线性插值方法线性组合相邻区域，有效解决了AHE中灰度值均匀区域的放大噪声问题。
3.2.1 基本原理
　　CLAHE的关键思想是如何限制对比度提高幅度，采用预定义的阈值裁剪直方图，如图3.1所示，直方图保留部分
斜度较小，因此累积直方图的斜度也被限制，由于图像对比大放大程度与变换函数斜度相关，变换函数的斜度又与
累积直方图的斜度成正比，从而限制了图像对比度[26]。

3.2.2 双线性插值法
　　CLAHE也需要划分小区域，对各个小块进行直方图均衡化，采用双线性插值的方法既能保证图像处理效果，又能
大幅提高算法计算时间，一举两得。双线性插值法步骤如下：
（1）首先将输入图像划分为大小相同的若干子块。
（2）下一步求取子块直方图，变换函数和累积直方图[27]。
　　（3）下图为双线性插值示意图，黑色区域为子块中心像素点，红色区域为图像角落像素点，绿色区域为图像边
界像素点，蓝色区域为非边界像素点。求解子块中各像素点的灰度变换函数时，若为中心像素点和角落像素点，取
块变换函数；若为边界像素点，则采用线性插值得到变换函数的值；若为中间像素点，采用双线性插值计算变换函
数。

3.3 实验结果与分析
　　本文处理降质图像算法的实验环境均是在处理器为Intel® Core™ i5-7200U CPU @2.50GHz(4 CPUs),内存
为8G的PC机上，操作系统为Windows 10家庭中文版64位，使用Matlab R2018b软件进行的。本实验使用的雾天图像集
部分源于网络。本节图像处理结果分析分为两小节，第一小节采用主观评价指标进行分析，第二小节采用客观评价
指标进行分析。
3.3.1 主观评价
　　图3.3展示了经过全局直方图均衡化处理前后图像和直方图的对比，可以观察到，雾天降质图像直方图在低灰度
区间频率较高，灰度级分布较为集中，处理后的图像灰度级分布更均匀。图3.4展示了经过限制对比度自适应直方图

均衡化处理前后图像和直方图的对比，处理后直方图保留了原先特征，斜度和原图直方图较为相似，保留了更多图
像细节。

图3.3 HE去雾效果与直方图对比

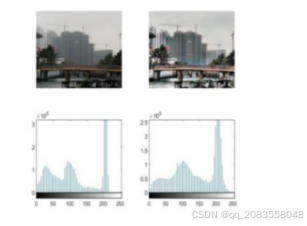
图3.4 CLAHE去雾效果与直方图对比
　　图3. 5和图3.6分别展示了两幅不同图像经过HE和CLAHE算法的去雾效果，（a）是降质图像，（b）是HE去雾图
像，（c）是CLAHE去雾图像。经过观察，（b）（c）两列图像整体对比度显著提升，图像较为清晰。相较而言，全
局直方图均衡化算法去雾不彻底，对于图像较亮和较暗区域会产生光晕和色彩失真的现象。由于全局直方图均衡化
对图像进行粗略的整体操作，必然存在缺陷，例如灰度级减少，图像高频部分细节缺失；频率较高的灰度级，会出
现过度增强的现象；天空区域出现光晕，处理后图像色调偏移等等。第三列限制对比度自适应直方图均衡化方法虽
然还存在一定程度色彩失真现象，但对此已经有很大改善，有效提升了对比度，色彩丰富性好，去雾效果更佳。
（a）降质图像 （b）HE （c）CLAHE

图3. 5直方图均衡化去雾效果对比图
（a）降质图像 （b）HE （c）CLAHE

图3. 6直方图均衡化去雾效果对比图
3.3.2 客观评价
　　本文第二章当中详细介绍了客观评价指标，亮度均值代表图像平均像素值，均值越大图像越明亮；信息熵可用
于衡量图像含有信息量的大小，信息熵越大等同于信息量越大；峰值信噪比用于比较去雾前后图像差异，数值越大
表示和原图相比有雾程度更小；结构相似性也需要将增强后的清晰图像和原始降质图像进行对比，结构相似性越
大，说明两幅图像结构越相似。
　　对图3.5和图3.6展示的图像，计算他们的客观评价指标，各项数据结果如表3.1所示。分析数据可以得出，不能
仅从亮度均值来对图像质量做出定论，因为有雾图像随着雾气加深，颜色会更加泛白。经过HE和CLAHE算法处理后，
图像的信息熵都有很大提升，符合人眼主观感受。峰值信噪比和结构相似性需要和原始图像进行对比，原始降质图
像会影响这两项的结果，对于图3.5来说，两项数据显示HE的效果更好，而对于图3.6来说，CLAHE的处理效果更优。

两种算法对原始图像都起到了一定程度的去雾效果，到底是以主观评价指标为主，还是客观评价指标为准，需要根
据不同的应用场景再作评判。

3.4 本章小结
　　本章重点研究直方图均衡化算法，首先对图像灰度直方图的概念做出阐述，接着详细分析了全局直方图均衡化
的基本原理和步骤。该方法原理简单，容易丢失很多细节信息。继而采用限制对比度直方图均衡化对降质图像进行
去雾操作，该方法和全局直方图相比，改善了色彩失真和噪声放大现象，图像更优质。

4 基于Retinex理论的雾天图像清晰化研究

上一章研究了基于直方图均衡化的雾天图像清晰化算法，属于基于非物理模型的图像增强手段，本章重点研究
Retinex理论，仍属于图像增强的范畴。首先对基础理论知识作出说明，着重研究了単尺度和多尺度Retinex算法，
通过实验分析其优缺点并做出改进。
4.1 Retinex理论
　　美国物理学家Edwin Land 基于人类视觉彩色恒常性提出了一种被称为Retinex的色彩理论[28]。该理论认为真
实图像取决于物体本质特性，不受环境影响。主要内容为以下两个方面：物体的颜色是由物体对红绿蓝三种波长的
光线的反射能力决定的，并非由反射光强决定；大气照射分量均匀与否不改变物体的颜色。
4.1.1 基本原理

图4.1 Retinex算法原理图
　　如图4.1所示，传统Retinex理论认为一幅图像可以由反射分量R和照射分量L的乘积表示。反射分量代表被拍摄
物体的本质特征，照射分量代表图像亮度范围，属于大气光的影响。如何从降质图像中准确去除照射分量的影响，
保留反射分量，是Retinex算法能否恢复清晰图像的关键。详尽数学转换流程如下：
（1）基于Retinex理论，输入图像
可以表示为：
（4.1）
式中，
为图像中的像素位置；
为输入图像；
为照射分量，代表大气环境光干扰；
为反射
分量，代表物体本质特征。

（2）变量的乘积可以转换成对数域变量的相加，由于人眼的视觉特性曲线与对数函数曲线十分相似，因此对数
域下的处理更符合人的视觉特性[29]：
（4.2）
（3）其中照射分量
可由包围函数
和输入图像
的卷积计算得到：
（4.3）
（4）结合公式（4.2）、（4.3）消除照射不均影响后，反射分量的数学描述为：
（4.4）
（5）对计算得到的对数域反射分量求指数运算，得到真实的反射分量

4.1.2 传统Retinex理论分类
　　传统Retinex理论可分为単尺度Retinex算法（SSR）、多尺度Retinex算法（MSR）、带颜色恢复的多尺度
Retinex算法（MSRCR）[30]。
　　高斯滤波器尺度的选取关乎能否在增强图像细节和保持图像色彩间保持平衡。SSR中高斯函数的尺度固定不变，
尺度越小，图像细节保持较好；尺度越大；图像色彩恢复越好。由于SSR难以保证去雾后图像细节特征明显且色彩真
实，研究人员后续提出了MSR算法和MSRCR算法。MSR对多个SSR进行加权求和，MSRCR引入色彩恢复因子记录原始RGB
三通道比例，以此控制色调。两者处理效果更好，但运算过程复杂，计算时间较长。
4.2 基于高斯滤波器的単尺度Retinex算法
　　単尺度Retinex算法是Jobsn等在Edwin的理论基础上提出，用高斯滤波器和输入降质图像进行卷积，再从降质图
像中去除该结果得到反射分量。
高斯包围函数公式如下：
（4.5）
式中， 为归一化常数； 为高斯尺度，高斯包围函数系数取值需满足下式：
（4.6）
　　高斯尺度的选取与图像去雾效果密不可分，关乎着去雾图像在细节保持方面和色彩保真方面平衡的程度。实验
时应通过多次调试来获得最合适的取值。
SSR算法的处理步骤如下所示：
（1）对原始图像进行颜色通道分解后做对数运算。
　　（2）选择合适的高斯尺度 ，必须满足式（4.6），由此得到高斯围绕函数
,利用高斯滤波器得到照度分

量
。高斯函数具体代码如下：
1.sigma=250;
2.F=zeros(N1,M1);
3.for i=1:N1
4. for j=1:M1
　　5. F(i,j)=exp(-((i-N1/2)^2+(j-M1/2)2)/(2sigmasigma));
6. end
7.end
8.F=F./(sum(F(😃));
（3）用logS-logL得到三个通道的反射分量
1.Ffft=fft2(double(F));
。具体代码如下：
2.DR0=Rfft2.*Ffft;
3.DR=ifft2(DR0);
4.DRdouble=double(DR);
5.DRlog=log(DRdouble+1);
6.Rr=Rlog-DRlog;
7.EXPRr=exp(Rr);
（4）对上面求出的反射分量再做指数运算。
（5）对反射分量进行对比度拉伸处理，公式如下：
（4.7）
其中，
指
中的最大值，
指
中的最小值。代码如下：
1.MIN = min (min (EXPRr));
2.MAX = max (max (EXPRr));
3.EXPRr = (EXPRr-MIN)/(MAX-MIN);
4.EXPRr=adapthisteq(EXPRr);
5.J(:,:,a)=EXPRr;
（6）进行通道融合，得到最终的反射分量

4.3 基于高斯滤波器的多尺度Retinex算法
　　単尺度Retinex算法只有一个滤波尺度，增强图像细节的同时必然会牺牲色彩保真度，多尺度Retinex算法利用
高斯函数与图像卷积，再对不同尺度的SSR进行加权平均运算得到去雾后清晰图像，运算公式如下：
（4.8）

式中
是高斯函数， 是尺度数量， 是各个尺度所占权重，需满足各个尺度权重和为1，即
，通常情况下对大，中，小三个尺度取等权重计算，即 =3，去雾效果较好，也能同时具备不同大小高斯尺度的优
点。
4.4 实验结果与分析
　　图4.4-图4.6为多尺度Retinex算法去雾结果，第一列为原始图像，第二列为增强后清晰图像。高斯尺度分别选
取 为128，256，512，尺度个数N=3，各尺度权重相同。
4.4.1 主观评价
　　观察图像可得，MSR算法去雾后图像清晰度大大提高，MSR算法保留了SSR算法的优点，细节信息保持较好的同时
确保图像色彩真实性。但对高亮度区域，如图4.5中的城市天空区域细节还原度不够，在图像的四周边缘和角落会出
现黑色阴影。部分区域还是会出现色彩失真的情况，例如第三幅图天际线区域，这是因为图像处理过程中改变了三
通道的颜色比例，因而可能会导致色彩失真。

图4.5 多尺度Retinex算法去雾效果对比图

Retinex理论能够提高图像对比度，但很容易导致图像色彩失真，且天空区域会出现光晕。多尺度Retinex理论
需要计算3个尺度，耗时相对较长。总的来说，Retinex理论难以在保持细节和色彩保真之间做出平衡。
4.4.2 客观评价
　　为了进一步体现算法的去雾效果，本小节使用亮度均值、标准差、信息熵这三种指标对多尺度Retinex算法的效
果进行评价，数据结果如表4.1所示，并绘制了柱状图，如图4.7所示。
　　由表4.1可得，使用MSR算法进行图像处理，恢复后图像的亮度均值得到了提升，表明去雾图像亮度增加，具有
更好的视觉效果；标准差得到增加，标准差越大，意味着图像像素动态范围越广泛，图像色彩更加丰富；信息熵增
大，表明去雾后的图像细节更完善。客观评价的结果与主观评价结果相符，证明了Retinex算法用于数字图像去雾处
理的有效性。

图4.7 客观评价指标柱状图
4.5 本章小结
　　本章重点研究Retinex理论算法，首先介绍了该理论的概念以及分类，其次详尽介绍了数学转换流程。接着重点
研究了単尺度Retinex（SSR）算法的原理与步骤。然后尝试使用多尺度Retinex（MSR）算法，对大中小三个尺度的
SSR算法进行加权融合。结果表明，改进后的MSR算法，综合了不同尺度SSR算法的优势，恢复的图像拥有更好的去雾
效果。

5 基于暗通道先验的雾天图像清晰化研究

本章研究的内容是基于物理模型的图像复原方法，深入分析图像降质根本原因，此类方法包括基于大气光偏振
信息、基于景物深度、基于先验信息的方法。本章重点研究基于暗通道先验的雾天图像清晰化算法，分析其原理和
步骤，并提出改进之处。

5.1 暗通道先验理论
　　He等人观察了大量的雾天图像，总结出暗通道统计规律，即无雾图像的绝大多数非天空区域，其三个颜色通道
中至少有一个亮度值趋于0[31]，意味着无雾图像的暗通道灰度图近乎全黑，而有雾图像的暗通道灰度图会出现白茫
茫一片。暗通道数学模型公式如下：
（5.1）
其中，
表示以 为中心的邻域，
表示一个颜色通道中 邻域内各点灰度值，
表示无雾图像
的
暗通道。

图5.1 图像暗通道对比图
　　图5.1（a）为无雾图像，观察其暗通道灰度图（b），在山脉和河流区域近乎全黑，与天空区域分界线明显；图
5.1（c）为有雾图像，其暗通道灰度图为（d），图像整体泛白，景物轮廓模糊。基于暗通道先验的雾天图像清晰化
算法就是以暗通道作为先验知识，结合物理模型求解其中重要参数，最终得到去雾后的清晰图像。
5.2 传统的暗通道先验理论算法实现
　　暗通道先验理论属于基于图像复原的雾天图像清晰化算法，利用大气散射模型进行反演去雾，在本文第二章中
详细的叙述了大气散射模型的物理构成，该模型是各种图像复原方法的理论基础，模型简化公式如下：
（5.2）
　　其中，
表示输入的降质图像，
表示去雾后清晰图像，
表示各点透射率， 表示大气光值。使用大
气散射模型进行反演就必须要先求出大气光值和透射率。暗通道先验理论方法利用暗通道作为先验知识，在求解过
程中起到了至关重要的作用。
5.2.1 暗通道先验理论算法处理步骤

整体代码如下所示，重要环节均以函数的形式调用：
1.function J = deHaze(im)
2.JDark = darkChannel(im);
3.A = atmLight(im, JDark);
4.transmission = transmissionEstimate(im, A);
5.tMat = transmission;
6.J = getRadiance(A,im,tMat);
7.end
（1）计算降质图像暗通道
根据式（5.1）求解暗通道
，提取邻域的窗口大小设置为15*15，进行两次最小值滤波。具体代码如下：
1.function JDark = darkChannel(im2)
2.[height, width, ~] = size(im2);
　　3.patchSize = 15; %the patch size is set to be 15 x 15
4.padSize = 7;
　　5.JDark = zeros(height, width); % the dark channel
　　6.imJ = padarray(im2, [padSize padSize], Inf); % the new image
7.for j = 1:height
8. for i = 1:width
　　9. patch = imJ(j:(j+patchSize-1), i:(i+patchSize-1)😅;
10. JDark(j,i) = min(patch(😃);
11. end
12.end
（2）计算大气光值A
　　求取大气光值A需要根据上一步中降质图像暗通道图，选定灰度值为前0.1%的点，在降质图像
个颜色通道内找到最大灰度值，最后取其均值作为A的估计值。具体代码如下：
1.function A = atmLight(im, JDark)
相应位置的三
2.[height, width, ~] = size(im);
3.imsize = width * height;
　　4.numpx = floor(imsize/1000); % accomodate for small images
　　5.JDarkVec = reshape(JDark,imsize,1); % a vector of pixels in JDark
　　6.ImVec = reshape(im,imsize,3); % a vector of pixels in my image
7.[JDarkVec, indices] = sort(JDarkVec);
8.indices = indices(imsize-numpx+1:end);
9.atmSum = zeros(1,3);
10.for ind = 1:numpx
11. atmSum = atmSum + ImVec(indices(ind)😅;
12.end
13.A = atmSum / numpx;
（3）粗略估计透射率
对式（5.2）左右两端同除大气光值，进行两次最小化操作：
（5.3）

根据暗通道计算公式（5.1），上式可进一步化简为：
（5.4）
其中，
为输入降质图像的暗通道。
　　晴朗天气下空气中也存在着许多小颗粒，人眼看向远处景物也会产生类似于雾的效果，为了使复原后的图像更
加真实自然，保留部分雾气，加入一个修正参数对透射率进行优化：
（5.5）
式中 范围为[0,1]，实验表明， 取值0.95是比较合适的。代码如下：
　　1.function transmission = transmissionEstimate(im, A)
　　2.omega = 0.95; % the amount of haze we’re keeping
3.im3 = zeros(size(im));
4.for ind = 1:3
5. im3(:,:,ind) = im(:,:,ind)./A(ind);
6.end
7.transmission = 1-omega*darkChannel(im3);
（4）优化透射率
　　使用粗略估计的透射率进行去雾，会使景物与天空交界处存在一条白色的线，在景深变化较大的地方处理不协
调，文献[32]提出使用软抠图算法将粗略估计的透射率进一步优化。软抠图算法使用的数学模型公式如下：
（5.6）
　　式中， 指的是原始输入图像，该模型将图像前后景进行了分离操作， 为图像前景的颜色， 为图像后景的颜
色， 表示前后景的合成系数，又指图像像素点的灰暗程度。上式与式（5.2）结构组成高度相似，为了快速求解上
式，令
为精细化后的透射率，
为原先粗略估计的透射率，构建了与式（5.6）相似的能量等式，并作最小化
操作，代价函数公式如下：
（5.7）
式中， 为修正系数， 为拉普拉斯矩阵，等式右边第一项为平滑部分，第二项为数据部分，矩阵 的定义为：
（5.8）
　　式中， 为窗口内像素点个数， 为克罗内克函数， 和 为原始图像在对应点的取值， 为图像像素的均
值， 为像素的协方差， 为归一化因子， 为3×3单位矩阵。求解式（5.8）得到精细估计的透射率：
（5.9）
式中， 和 为同样大小的单位矩阵， 为调整精度的因子。
（5）复原清晰图像
求得大气光值和透射率后，根据大气散射模型复原图像：

（5.10）
其中 是为了防止透射率估计过小使图像泛白而设置的阈值，通常取
。具体代码如下：
1.function J = getRadiance(A,im,tMat)
2.t0 = 0.1;
3.J = zeros(size(im));
4.for ind = 1:3
　　5. J(:,:,ind) = A(ind) + (im(:,:,ind) - A(ind))./max(tMat,t0);
6.end
7.J = J./(max(max(max(J))));
5.2.2 暗通道先验算法效果分析

图5.3 城市图像暗通道处理效果
　　暗通道先验去雾算法响应十分快速，但是复原后清晰图像整体亮度偏低，如图5.3（b）、（c）所示。求取降质
图像暗通道时可能产生块状效应，如图5.3（d）所示，粗略估计透射率后复原的图像存在缺陷，在景物和天空交界
处会出现带状白条，如图5.3（b）所示。经过软抠图算法优化透射率后，景物与天空衔接处更加自然，如图5.3
（c）所示，但是软抠图算法涉及大量稀疏矩阵运算，计算量非常大，算法耗时长，实时性差。
　　总的来说，传统的暗通道先验算法的原理推导简明易懂，处理效果真实自然，图像细节处也很完善，但同时也
存在着不足之处，提升图像亮度、优化透射率和改善算法效率将是进一步优化的方向。
5.3 改进的基于引导滤波的暗通道先验算法
　　传统的暗通道先验算法在处理大面积天空区域和白色物体区域时，会出现去雾不彻底的情况，在景物与天空交
界处会出现带状白条。引导滤波（Guided image filter,GIF）具有很好的边缘保持特性，利用引导滤波对大气散射
模型中的透射率进行优化，能够避免图像复原后产生伪边缘，亮度分布不均的现象。
5.3.1 引导滤波原理
　　引导滤波是个线性滤波过程，针对输入图像 ，利用引导图像 ，进行引导滤波得到输出图像 。对于 位置的像
素点，得到的滤波输出是加权平均值 ，如下式所示：
（5.11）

其中，表示像素点的位置，
表示与引导图像有关的滤波函数。
假设输出图像和引导图像在滤波窗口
上存在局部线性关系：
（5.12）
　　其中，k为窗口中心点位置，i作为像素点索引，对于一个半径r确定的窗口
,
,
是确定的常数，对上式进
行求导，得到下式：
（5.13）
　　由上式可见，在局部线性区域，若I细节边缘存在梯度，则也能获取相同梯度信息，从而保持该边缘不变，可
见该算法的边缘保持特性较好。
　　只要求解出系数
,
就能得到输出图像q，下面把
,
的求解转化为最优问题，将输入图像P中非边缘区域又
不平滑的地方视为噪声n，满足
，该优化问题处理的目标是最小化这个噪声。对于每一个滤波窗口，在
最小二乘意义上的优化可以表示为:
（5.14）
（5.15）
　　为了避免
过大而引入正则化参数，在引导滤波中使用相同的,不考虑像素值的差异，进一步得到滤波窗口
内的代价函数：
（5.16）
对等式两边求导，得到
的表达式：
（5.17）
（5.18）
（5.19）
　　其中，
为窗口内像素数量；
为输入图像在滤波窗口中的方差；
为输入图像在滤波窗口中的均值，
； 为输入图像各像素值平方在滤波窗
；为引导图像在滤波窗口中的均值，
口中的均值，
；
为输入图像和引导图像像素点乘积在滤波窗口中的均值，

。
每个像素点会处于不同滤波窗口中，对各滤波窗口的线性系数取平均得到最终结果：
（5.20）
其中
，
。
　　原始输入图像经过引导滤波得到图像基础部分，输入图像与基础部分的差值成为图像残差，即细节部分，再乘
增强系数并加到原始图像上，以此增强细节。许多研究人员对基础层和细节层采用不同的手段分别处理，最后再加
权融合，能够获得更好的效果。
　　当引导图像是原图时，引导滤波就成为边缘保持滤波器。将引导滤波和暗通道先验相结合，以原图灰度图作为
引导图像I，对简要估计后的透射率t(x)进行优化。具体代码如下：
1.function q = guidedfilter(I, p, r, eps)
2.[hei, wid] = size(I);
3.N = boxfilter(ones(hei, wid), r);
4.mean_I = boxfilter(I, r) ./ N;
5.mean_p = boxfilter(p, r) ./ N;
6.mean_Ip = boxfilter(I.p, r) ./ N;
7.cov_Ip = mean_Ip - mean_I . mean_p;
8.mean_II = boxfilter(I.I, r) ./ N;
9.var_I = mean_II - mean_I . mean_I;
10.a = cov_Ip ./ (var_I + eps);
11.b = mean_p - a .* mean_I;
12.mean_a = boxfilter(a, r) ./ N;
13.mean_b = boxfilter(b, r) ./ N;
14.q = mean_a .* I + mean_b;
15.end
5.3.2 自动色阶算法
　　由于经过暗通道先验算法处理后的图像普遍偏暗，选择采用自动色阶算法修正去雾图像的明暗分布，以获得更
好的视觉效果。
　　自动色阶的原理思想是将三个通道分开处理，各自计算当前颜色通道的最大值和最小值，设定阈值并消除。对
各通道建立分段线性映射关系，重新按比例分配至[0,255]范围内，得到颜色增强后的图像。
使用引导滤波和自动色阶改进的暗通道先验算法流程图如图5.4所示：

图5.4 改进的暗通道先验算法流程图
5.4 实验结果与分析
（c）为结合引导滤波和暗通道复原图像，
（d）为使用自动色阶算法增强后的图像。由下图可见，引导滤波对透射率进行优化，减轻了景物与天空交界处出现
的带状白条现象，但是天空区域仍有光照不均的现象。和软抠图算法相比，程序运行时间大大减少，实时性增强，
图像效果和软抠图近似，但细节部分会产生模糊。自动色阶算法对图5.5颜色调整效果较好，但该算法自适应性较
差，对如图5.6存在大片天空区域的图像颜色调整效果一般。对于图5.7，经过处理后，图像对比度得到提升。
图5.5 结合引导滤波和暗通道去雾效果对比
图5.6 结合引导滤波和暗通道去雾效果对比
图5.7 结合引导滤波和暗通道去雾效果对比

暗通道
引导滤波
自动色阶
原图
16.6064
17.2477
17.9089

0.8698
0.8917
0.8947
1
图5.6

暗通道
63.861
2.8065
2.7785
2.9221
10.2547
10.2504
13.5013
0.5896
0.593

图5.7
引导滤波
自动色阶
63.6403
91.3473
0.7748
　　从表5.1分析可得，基于暗通道先验的算法去雾后清晰图像的信息熵都比原始图像的信息熵大，可见复原图像信
息量增大；改进算法得到的结构相似性数值更接近1，优于传统的暗通道先验算法；两种方法处理后，图像亮度均值
大幅下降，图像整体颜色变暗，可以采用自动色阶算法增强其亮度分量，能够获得更佳的视觉效果。
5.5 本章小结
　　本章重点研究基于暗通道先验的雾天图像清晰化技术，首先通过无雾图像和有雾图像的对比阐述了暗通道的概
念，接着详细叙述了该方法实现的步骤，同时列出了主要功能的程序代码。在优化透射率估计步骤中，针对软抠图
法占内存大耗时长的缺点作出进一步改进，使用引导滤波算法进行替代，并使用自动色阶算法调整图像的颜色，该
方法得到的图像去雾效果较好，实时性强。

6 基于GUI的雾天图像清晰化系统设计

MATLAB是一款功能非常强大的数学软件，利用MATLAB GUI（Graphical User Interface）和Image Processing
Tool-box可以设计一个雾天图像清晰化系统。该系统能够实现雾天降质图像的清晰化操作，具体功能有：采用全局
直方图均衡化、多尺度Retinex理论算法、改进的基于引导滤波的暗通道先验理论三种方法，在窗口中显示增强或者
复原后的清晰图像；在去雾评价指标对比界面，能够显示本文选取的客观评价指标数值；针对直方图均衡化算法，
还能进行处理前后直方图的对比；可以编译成.exe执行文件，不需MATLAB环境也可运行。该系统具有良好的交互
性，能够更直观地展现去雾算法的优劣，在未来有升级需求时也易于进行功能扩展。
6.1 MATLAB GUI介绍
　　MATLAB 图形用户界面是以图形样式显示的，能够进行人机交互的界面。有两种制作GUI界面的方法，直接使用
底层代码进行设计，或是使用便捷的GUIDE命令创建，后者减少了冗余的代码编程，给使用者带来了更加便捷的体
验。GUI提供了多种图形控件，直接拖动相应种类的控件，双击可以设置所需属性、更改显示字符、重新定义标记。
通过在回调函数中编写程序，来实现各控件对应的功能。总而言之，该系统无论是在视觉上还是操作上，用户都能
获得较好的使用感。整体设计流程如图6.1所示。

图6.1整体设计流程图
6.2 雾天图像清晰化系统总体设计
6.2.1 系统界面设计
　　雾天图像清晰化系统由三大模块构成，分别是去雾算法效果对比界面、客观评价指标对比界面、直方图对比界
面，下面将对界面设计进行介绍。
（1）去雾算法效果对比界面
　　该界面主要由图像显示区和功能选择区两部分构成，如图6.2所示，包含了静态文本，按钮，面板，坐标区四种

控件，在功能选择面板中，“打开”按钮能将图像显示在axes1坐标轴中；单击“直方图均衡化”按钮，结果将显示
在axes2区域中；单击“Retinex理论”按钮，结果将显示在axes3区域中；单击“暗通道先验”按钮，结果将在
axes4区域中显示；“清空”能清除显示区域的图像；“截图”能截取系统当前图像并保存在文件夹中；单击“退
出”按钮，退出系统。

图6.2 去雾算法效果对比界面设计图
（2）客观评价指标对比界面
　　该界面由图像与数值显示区和功能选择区构成，如图6.3所示。对功能选择区的控件进行操作，原始图像打开后
将显示在axes5中；在下拉菜单中可以选择去雾算法，对应的去雾图像将显示在axes6中；单击“客观评价指标”按
钮，数值会显示在左侧静态文本框内；单击“清空”按钮，将图像与数值显示区的信息清空，可以重新选择图像；
单击“退出”按钮，退出系统。

图6.3 客观评价指标对比界面设计图
（3）直方图对比界面
　　在菜单栏中“界面选择”单击“直方图对比”界面，选择所需处理的原始图像，会直接生成经直方图均衡化处
理后的直方图对比图，效果详见6.3小节。
6.2.2 系统软件设计
　　本文采用GUIDE命令创建GUI界面，界面设计完成后，单击运行，保存为DefogSystem.fig文件，自动生成
DefogSystem.m文件，.m文件中包含了opening，output，callback等函数，在各控件的回调函数中编写相应程序就
能够实现所设计的功能。值得注意的是，如果变量要在不同回调函数之间进行调用，需要给句柄赋值，并更新结构
体。完整程序见附件，下面列举重要段落进行说明：
（1）界面切换部分
　　在系统界面设计时，把各控件放到了相应面板中，成为其子元素，通过设置面板visible属性为on/off，即可设
置该面板仅在需要时可见。具体代码如下：
　　1.function interface1_Callback(hObject, eventdata, handles)
2.set(handles.uipanel2,‘visible’,‘on’);
3.set(handles.uipanel3,‘visible’,‘on’);
4.set(handles.uipanel4,‘visible’,‘off’);
5.set(handles.uipanel5,‘visible’,‘off’);
（2）去雾算法部分
　　本设计采用了3种去雾算法，在回调函数中调用相应程序即可，注意需要更新结构体中变量，以暗通道先验算法
为例，代码如下：
　　1.function HE_Callback(hObject, eventdata, handles)
2.if handles.Img1==0
3. msgbox(‘请先选择降质图像’,‘提示’);
4. return;
5.else
6.I=handles.Img1;
7.In=histequal(I);
8.handles.Img2=In;
9.guidata(hObject,handles); %更新结构体；
10.axes(handles.axes2);
11.imshow(In);
12.end
（3）下拉菜单部分
下拉菜单用于选择去雾算法，采用switch循环语句，代码如下：
　　1.function popupmenu1_Callback(hObject, eventdata, handles)
2.pnum=get(handles.popupmenu1,‘value’);
3.switch pnum
4. case 1
5. I=handles.Img1;
6. In=histequal(I);
7. handles.Img5=In;
8. guidata(hObject,handles); %更新结构体；
9. imwrite(In,‘imgforevalue.jpg’);
10. axes(handles.axes6);

11. imshow(In);
12. case 2
13. %略
14. case 3
15. %略
    16.end
    （4）显示客观评价指标部分
    单击“客观评价指标”按钮能将数值显示在静态文本框内，其tag记为evaluation，具体代码如下：
    　　1.function evaluation_Callback(hObject, eventdata, handles)
    2.I=handles.Img1;
    3.I=rgb2gray(I);I=double(I);
    4.[m,n]=size(I);
    5.imglm=(1/(m*n))*sum(I(😃);
    6.set(handles.value1,‘string’,num2str(imglm));
    7.imgstd=std(I(😃,1);
    8.set(handles.value3,‘string’,num2str(imgstd));
    9.k=3;
    10.ie = IE(I,k);
    11.set(handles.value5,‘string’,num2str(ie));
    12.set(handles.value7,‘string’,‘/’);
    13.set(handles.value9,‘string’,‘/’);
    6.3 雾天图像清晰化系统的运行效果
    本系统设计是针对单幅图像进行清晰化处理，下面按照涉及的功能进行描述：
    6.3.1 去雾算法效果对比界面
    该界面为系统打开时的默认界面，能同时显示三种去雾算法对比图。
    　　（1）打开图像：单击“打开”按钮，展示载入图像的路径，程序中设置了选择打开.jpg格式的图像，如图
    6.4。
    　　（2）图像显示与去雾处理：雾天图像在axes1区域中显示；单击“直方图均衡化”按钮，结果将在axes2区域中
    显示；单击“Retinex理论”按钮，结果将在axes3区域中显示；单击“暗通道先验”按钮，结果将在axes4区域中显
    示，效果如图6.5。
    　　（3）截图与清空：单击“截图”按钮可以将系统展示界面保存到文件夹中；单击“清空”按钮，可以清除当前
    区域内的图像。
    

图6.5 雾天图像清晰化系统的运行效果示意图
6.3.2 客观评价指标对比界面
切换界面需要点击菜单栏中的“界面选择”，点击“客观评价指标”按钮，界面效果如图6.6所示。
（1）打开图像：单击“打开”按钮，原始雾天图像将显示在axes5区域。
（2）去雾算法选择：打开下拉菜单栏，选择相应的去雾算法，恢复图像将显示在axes6中。
（3）计算客观评价指标：单击“客观评价指标”按钮，计算各指标数值并显示在左侧静态文本框内。
（4）清空：清除左侧图像和数据。
（5）退出：退出整个系统。

图6.6 客观评价指标对比界面效果示意图
6.3.3 直方图对比界面
　　在菜单栏“界面选择”点击“直方图对比”按钮，选择要处理的图像，直接生成直方图均衡化算法处理前后的
直方图对比图，效果如图6.7所示。

图6.7 直方图对比效果示意图
6.4 本章小结
　　本章主要基于MATLAB GUI设计了雾天图像清晰化系统，首先对GUI界面以及设计流程进行简要介绍，接着重点介
绍了系统总体设计，分为界面设计和软件设计部分，最后对系统的操作步骤和运行效果做出了详细描述。该系统具
有界面友好，操作简单，交互性强，易于扩展的特点，更方便地展示了去雾算法的效果，具有一定的实用性。

7 总结与展望

随着计算机视觉和数字图像处理领域的迅猛发展，交通监控、卫星遥感、自动驾驶、军事侦察等各种智能监测
系统已经渗透进我们的生活。然而在实际应用中，图像采集设备成像会受到诸多不利因素影响，例如雾天条件下，
图像的清晰化程度降低，对比度下降。图像质量的下降会影响智能监测系统的正常运行，从而干扰人们的正常生
活。由此可见，进行雾天图像清晰化研究对于实际生产生活有重要价值。
7.1 总结
　　本文重点针对三种去雾算法进行了深入研究和对比，认真总结了各自的优缺点，提出改进之处，本文的主要工
作如下：
　　（1）前期广泛阅读文献后，本文首先总结了去雾算法的背景意义和该领域研究现状，随后阐述了雾天成因、图

像退化特征、大气散射模型、主客观评价指标等基础理论知识。
　　（2）直方图均衡化算法方面，首先简要阐述了直方图的概念，接着详细叙述了全局直方图均衡化的原理步骤。
针对该方法处理全局时产生色调失真的问题，结合局部直方图均衡的优势，采取限制对比度直方图均衡化方法加以
改进。最后从主观评价指标和客观评价指标两方面对效果做出评定。两种算法都有一定程度的去雾效果，相比而
言，限制对比度自适应直方图均衡化算法改善了色彩失真和噪声放大现象，视觉效果更佳。
　　（3）Retinex理论算法方面，首先阐明了基本原理与算法分类，接着重点研究了単尺度Retinex（SSR）算法的
原理与步骤。然后尝试使用多尺度Retinex（MSR）算法，对大中小三个尺度的SSR算法进行加权融合。结果表明，改
进后的MSR算法，综合了不同尺度SSR算法的优势，更好保持图像细节的同时改善了色调失真的情况。
　　（4）基于暗通道先验的雾天图像清晰化算法方面，细致地分析了该类方法的基本原理和实现步骤，利用计算得
到的暗通道值去估计大气光强和各像素点透射率。接着重点研究了透射率估计的优化方法，针对软抠图算法优化时
计算时间过长的问题，使用引导滤波算法对透射率进行改善，针对暗通道处理后图像过暗，提出用自动色阶算法调
整颜色。经过实验分析，改进算法复原图像效果较好，实时性强。
　　（5）在本文的研究基础上，基于GUI设计了雾天图像清晰化系统，包括去雾算法效果对比、客观评价指标对
比、直方图对比三个模块，该系统具有良好的交互性，能够更直观的展现去雾算法的优劣，在未来有升级需求时也
易于进行功能扩展。
7.2 展望
　　本文在雾天图像清晰化研究方面取得了一定成果，虽然实现了三类去雾算法并做出微小改进，但由于时间限制
和学术水平限制，所作的研究还有许多值得改进的地方：
　　（1）在传统Retinex理论中，高斯滤波器仅考虑像素点间的距离，而不考虑像素点本身灰度值相似程度，在像
素值突变的图像边缘处，模糊处理会损失图像细节，后续研究可以选取具有较好边缘保持能力的双边滤波器进行改
进。
　　（2）在暗通道先验算法中，采用引导滤波替代软抠图算法优化透射率，是否能采用其他算法估计出更准确的透
射率。此外，可以尝试分割图像中天空区域和景物区域，分别进行处理。
　　（3）本文使用的算法主要针对单幅图像，建立了自己的图像集，若在需要大批量处理图像的情况下，如何提高
算法的效率值得进一步研究。
　　（4）目前图像处理领域没有通用的质量评价标准，本文中选取合适的指标进行评判，各个学者选择的评价指标
存在差异。

致谢

清风锁不住流云，流云带走了岁月。行文至此，落笔为终，我的大学生活即将落幕。时间仓促，还未来得及细
细品味就已经飞快流逝，时光如烟火，满目繁华，皆是回忆。回顾大学以来的学习生活，我也一直在努力，一直在
成长。总觉得人生逆旅，命运多舛。但回首望去，发现幸运仍一直陪伴着我。无论何时何地，总有良师益友，在人
生的重要关口，伴我成长，与我同行。从海大到天大，充盈在内心的更多的是感激。我要向所有曾陪伴、关心、照
顾我的人道一声感谢，让我能够在这一路上勇往直前，与君相识，三生有幸。
　　 桃李不言，下自成蹊。首先，我要特别感谢我的论文指导老师袁琦教授。老师严谨的治学态度、严密的思维逻
辑、睿智宽容的学者风范和低调务实的为人原则让我在学习和做人方面都终身受益。论文从选题、开题、撰写成文
到最后的定稿，无不得益于袁琦教授的悉心指导。我将牢记老师之教诲，奋力拼搏，为实现中华民族伟大复兴贡献
青春力量。
　　 焉得萱草，言树之背。我也要特别感谢我的父母和家人，父母之爱女，则为之计深远，感谢父母20多年对我的
无微不至的照顾与支持。二十余载，让我能暖衣饱食，无后顾之忧！我将会带着他们的爱奋力前行，愿家人们身体
健康，幸福美满。
　　 岁月虽清浅，时光亦潋滟。无论是海大还是天大，我都要感谢我的朋友们，让我在千里之外的他乡感受到了温
暖。感谢你们的包容关怀。海内存知己，天涯若比邻。感谢海大天大的同学们，山水一程，三生有幸，愿此去前程
似锦，再相逢依旧如故。
　　 学贵得师，亦贵得友。感谢海大和天大的所有老师。在求学的日子里，我一直被温暖环绕。感谢专业课老师的
倾囊相授，让我不仅学习到了知识，更让我领悟了学者风范。愿各位老师工作顺利，身体健康。
　　 山水相逢，终有一别。在今后的学习和工作中，我会继续砥砺前行，脚踏实地，仰望星空，踏上更为广阔的人
生。骄阳似火的海甸岛，花堤蔼蔼的卫津路，我们后会有期。