Tensorflow 学习（一） DNN的前世今生（一）加源代码展示

这篇博客呢，主要记录的是自己对DNN的理解，然后呢，还记录了一下比较前沿的DNN的理论 ELU，Dropout,动量法，RMSProp。反向传播算法呢，由于优快云上面街上的已经很多了，不在这篇的讨论范围之类，这篇博客主要参考的台大李宏毅的机器学习、以及DeepLearning 这本书吧。

我只是知识的搬运工 JXinyee，嘿嘿

在此附上李宏毅老师的个人主页，讲的非常非常好http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html

我们刚开始在使用深度学习的使用，大多数人用的都是手写数字识别这个数据集。而且这个手写数字识别大概需要3个隐藏层就能达到92%以上的准确率。但是随着时代进步，社会发展。如果你需要解决非常复杂的问题，例如语音识别中的上百种语言，无数多个单词该怎么办？ 这时候就要训练更深的 DNN，也许有 10 层，每层包含数百个神经元，通过数十万个连接来连接。这就引入了梯度爆炸的问题了，如果你对此抱有怀疑，不妨看一下下面这个函数。

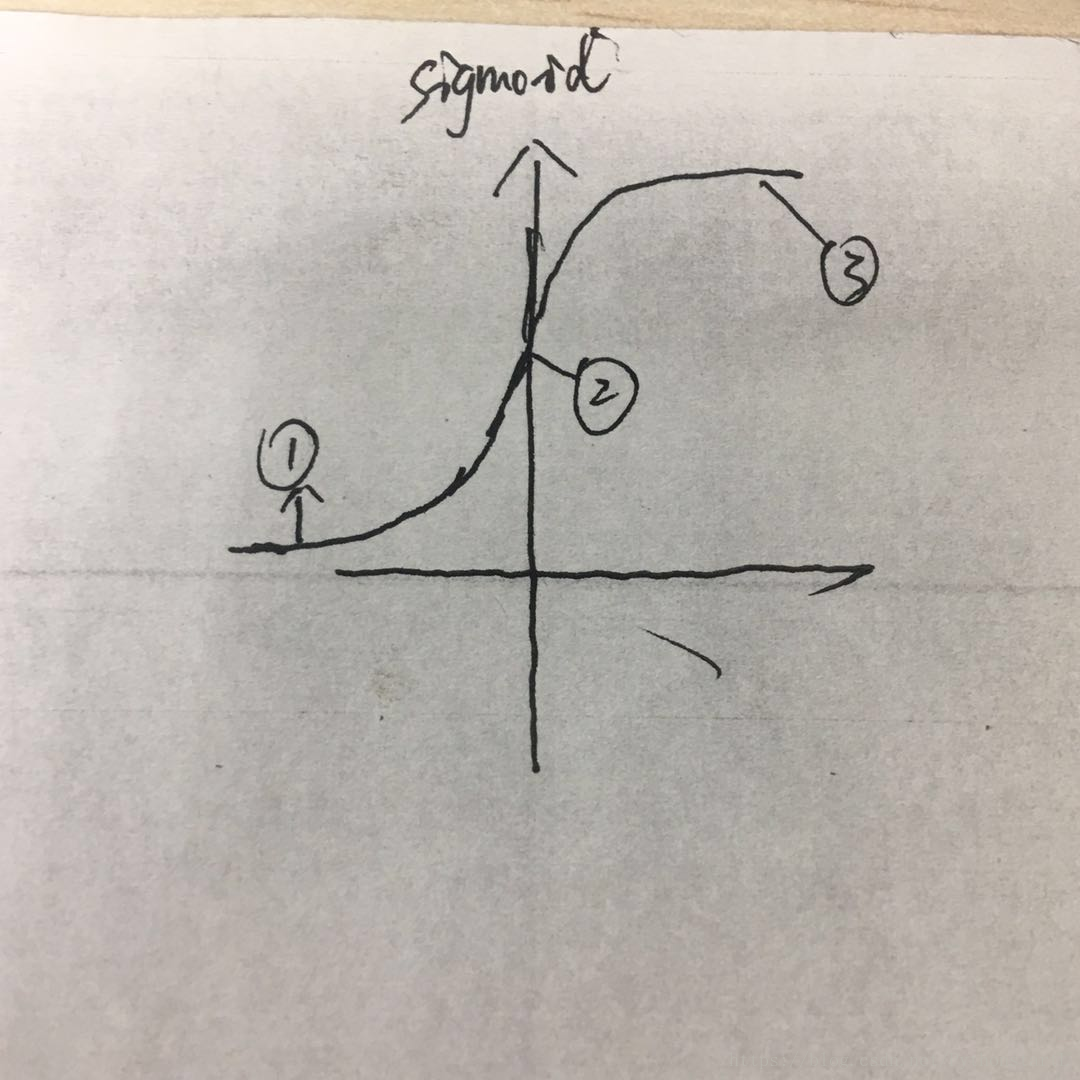
很长一段时间人们用sigmoid函数作为激活函数，人们认为这种连续性的函数似乎能模拟人的大脑神经元的活动，当然事实上，后来证明relu更好。

1 sigmoid 函数的y值 对应的都是正的，均值为0.5，这会让训练得到的方差随着层数递增不断加大，人们后来通过这个提出了tanh函数 均值为0，效果确实要好一些

2.如上图所示，函数上分别有1、2、3三个点当sigmoid函数的目标点是1的时候，但是你现在处于3这个位置时。你会发现从3用梯度下降多么多么的艰难，因为3的梯度接近于0，这也会出现，我们发现训练着训练着发现，越接近输入层的伸进网络的权重越发不动了，梯度似乎“消失”了，这会导致训练深层的神经网络，训练会非常缓慢，这也是一段时间内，神级网络臭名昭著的原因。

解决梯度消失的方法（Xavier初始化）

Glorot 和 Bengio 在2015年的一篇论文中认为，我们需要每层输出的方差等于其输入的方差。（这里有一个比喻：如果将麦克风放大器的旋钮设置得太接近于零，人们听不到声音，但是如果将麦克风放大器设置得太大，声音就会饱和，人们就会听不懂你在说什么。神经网络也是如此，我们既不希望权重在传递的过程中消失了，也不希望他爆炸饱和。

于是他们提出了一个公式：

他们发现随机初始化连接权重必须如公式 11-1 所描述的那样。其中n_inputs和n_outputs是权重正在被初始化的层（也称为扇入和扇出）的输入和输出连接的数量。具体的证明公式，请看Glorot 和 Bengio 的论文。现在好多都是这么干的。

另外Glorot 和 Bengio 在 2010 年的论文中的一个见解是，消失/爆炸的梯度问题部分是由于激活函数的选择不好造成的。 在那之前，大多数人都认为，如果大自然选择在生物神经元中使用 sigmoid 激活函数，它们必定是一个很好的选择。 但事实证明，其他激活函数在深度神经网络中表现得更好，特别是 ReLU 激活函数，主要是因为它对正值不会饱和（也因为它的计算速度很快）。而且也很简单，这也是大自然的神奇之处，越简单的函数泛性反而越好。

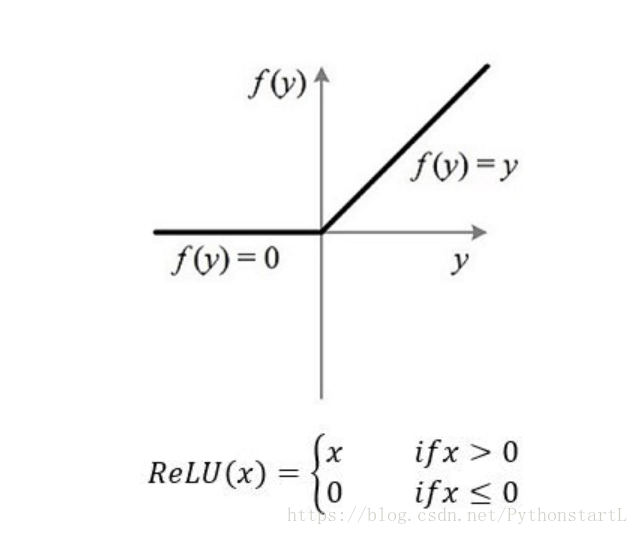
首先relu这个函数呢，我们可以看到求导非常的简单，而且是固定值，不会出现梯度消失的问题，在另一方面，relu能够更好的拟合函数，包括非常复杂的函数。拿李宏毅老师上课给的一个例子：

对于一个给定的函数f1,现在我们要找一个函数f2去拟合它，我们不妨假设这俩个