排序算法

排序算法

关心算法的两点：
1.时间复杂度
2.稳点性（相同值的元素维持原有次序）
1.用户体验
2.减少计算机开销
判断方式：是否相邻交换

冒泡排序：
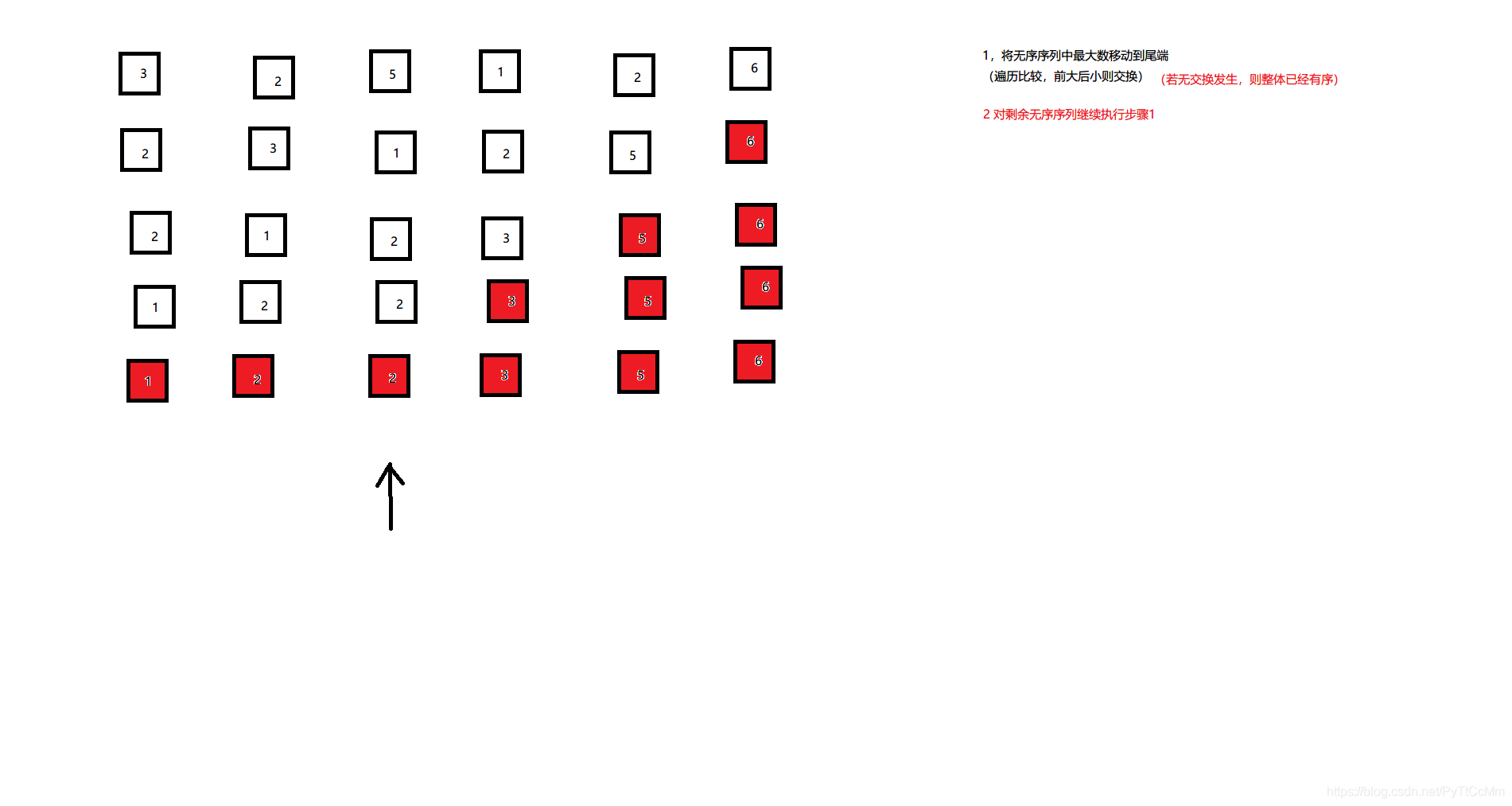
1.将无序序列最大的元素移动到尾端（遍历比较，前大后小则交换）
若本次遍历没有交换发生，则认为全部有序
2.对剩余无序序列重复步骤

时间复杂度：O（n^2）
最优时间复杂度 ：O（n）
稳定性 ：稳定

def Bubble_sort(li):
    """冒泡排序"""
    n= len(li)
    # j 表示无序序列的长度
    for  j in range(n,1,-1):
        swap_count = 0
       for i in range(0,j-1):
           if li[i] > li[i+1]:
              li[i],li[i+1] = li[i+1],li[i]
           swap_count += 1
      #如果本次交换没有发生，则认为这个序列是有序
        if 0 == swap_count :
          return
if  __name__ == "__main__":
   li = [1,2,3,5,9,7,5,6,1,5,5]
   Bubble_sort(li)
   print(li)

选择排序
1.遍历比较，选出最小值并记录该值索引（小则更新）
2.交换最小值和无序序列首个元素
3.对剩余无序序列重复步骤1，2
时间复杂度：O（n^2）
稳定性： 不稳定

def select_sort(li):
  n = len(li)
    # 1.遍历比较，选出最小值并记录该值索引（小则更新）
  # j 代表当前有序序列的长度
  for j in range(0,n-1):
      min_index = j
      for i in range(j+1,n):
          # 2.交换最小值和无序序列首个元素
          if li[i] < li[min_index]:
              min_index = i
      # 至此，最小索引已经找到，交换值
      li[min_index],li[j] = li[j],li[min_index]
      # 3.对剩余无序序列重复步骤1，2
if __name__ == '__main__':
  li= [1,2,5,9,7,6,7]
  select_sort(li)
  print(li)

插入排序：（对大概有序的序列效果好）
1.将无序序列首个元素向前插入有序序列（反向遍历）
若没有发生前大后小，则步骤结束
2.对剩余无序序列下重复步骤1
时间复杂度 ：O（n^2）
最优时间复杂度：O（n）
稳定性 ：稳定

def insert_sort(li):
    n = len(li)
    # j 代表无序序列的首个元素
    for j in range(1,n):
        # 将无序序列首个元素向前插入有序序列（反向遍历，前大后小则交换）
        for i in range(j,0,-1):
            if li[i-1] > li[i]:
                li[i],li[i-1]= li[i-1],li[i]
            else:
            # 若没有发生前大后小，则步骤1结束
               break
         # 对剩余无序序列[2:n]重复步骤1
if __name__ == '__main__':
    li= [5,2,1,9,7,3,8]
    insert_sort(li)
    print(li)

希尔排序
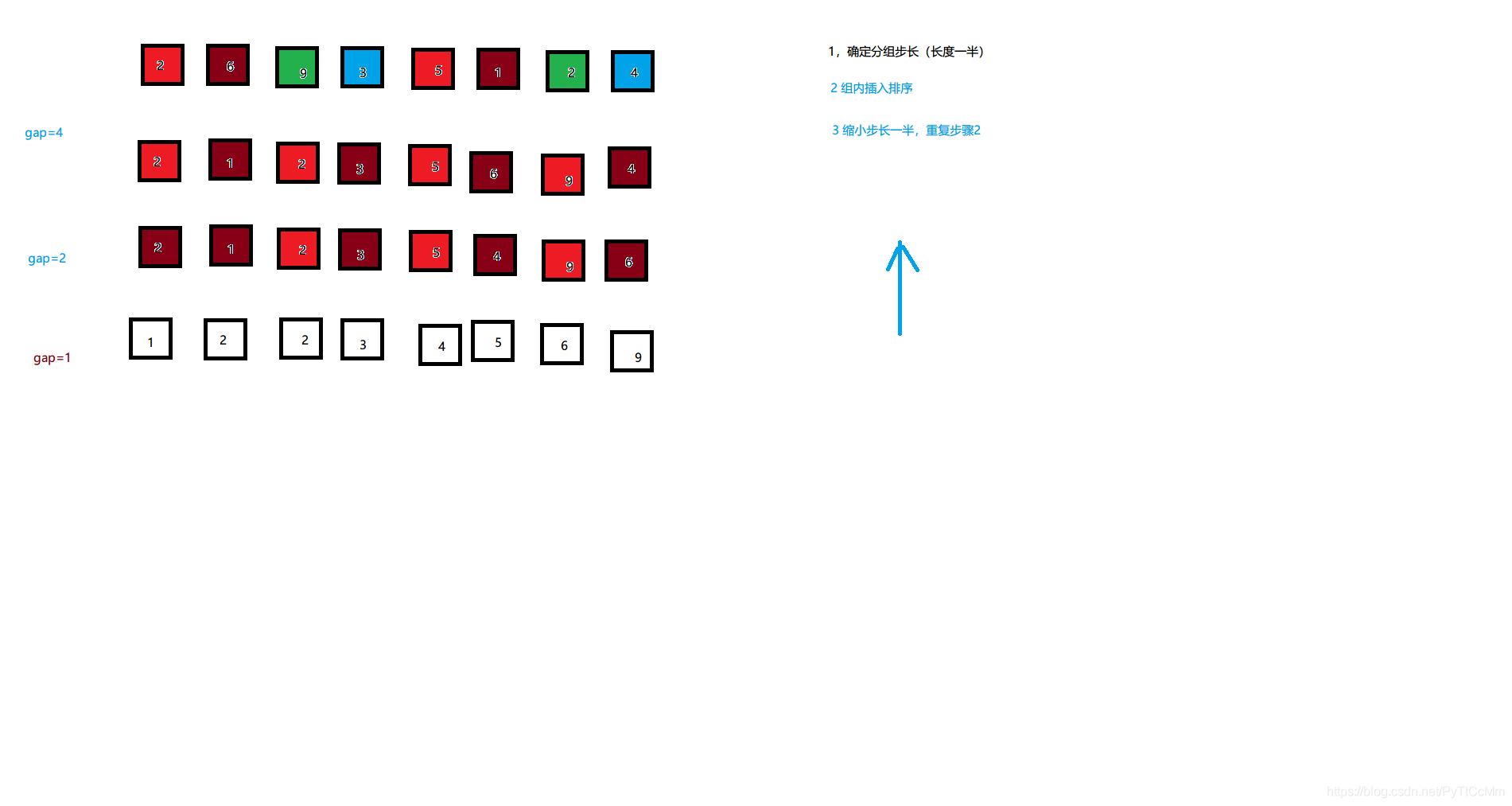
1.确定步长分组（长度的一半）
2.组内插入排序（将插入排序的所有1等量替换成步长）
3.缩小一半步长，重复步骤2
平均时间复杂度：O（n^1.3~2）
最优时间复杂度：O（nlogn）
最坏时间复杂度：O（n^2）
稳定性： 不稳定

def shell_sort(li):
 n = len(li)
 # 确定步长分组
 gap = n // 2
 while gap >0:
     # j 表示无序序列的首个元素
     for  j in range(gap,n):
         for i in range(j,0,-1):
             if li[i-gap]>li[i]:
                 li[i-gap],li[i] = li[i],li[i-gap]
             else:
                 break
     gap = gap // 2
if __name__ == '__main__':
  li = [5,4,1,2,9,8,3]
  shell_sort(li)
  print(li)

快速排序：
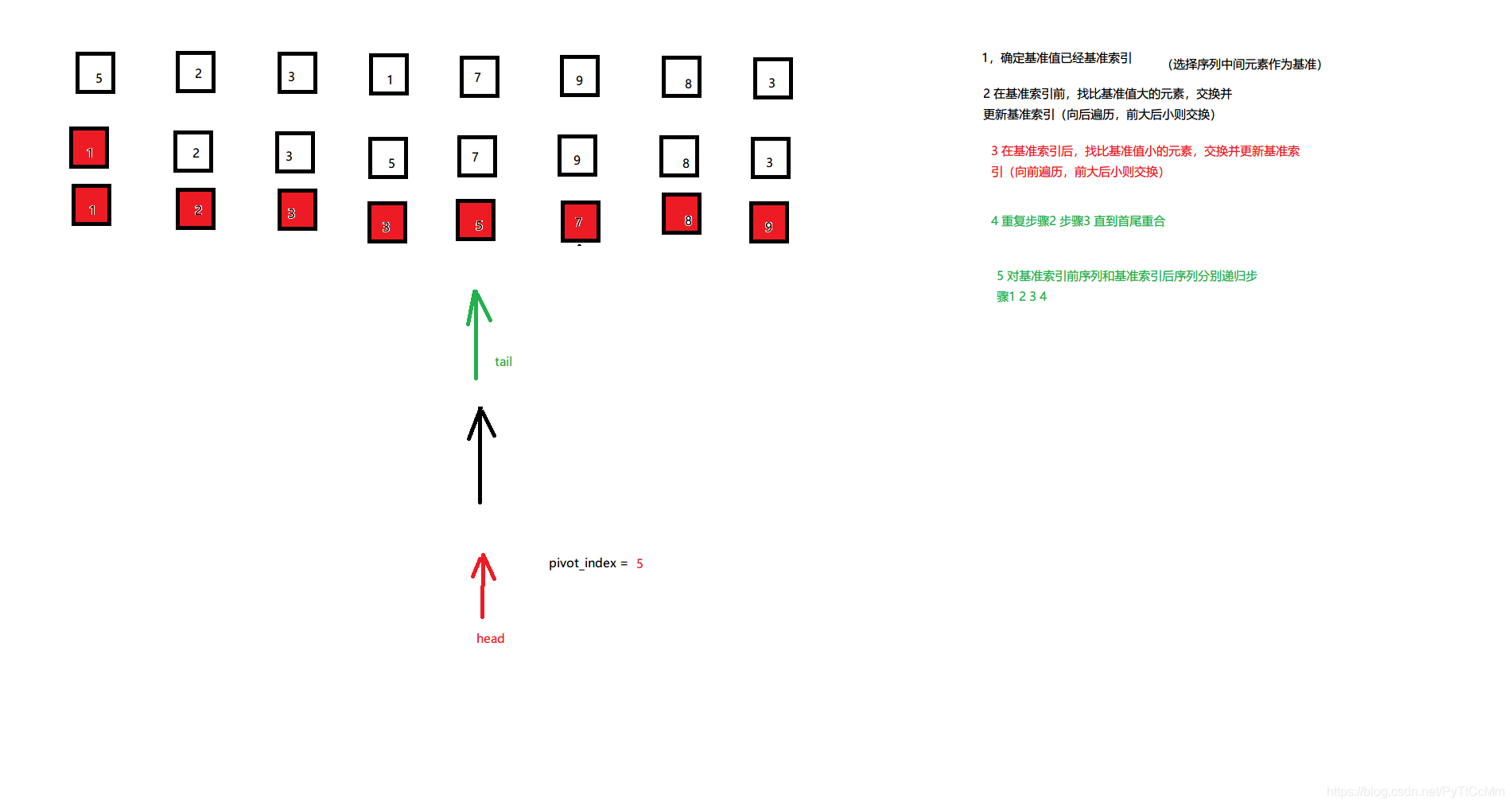
1.确定基准索引
2.在基准索引前找比基准值大的元素，交换并更新基准索引 （向后遍历，前大后小则交换）
3.在基准索引后找比基准值小的元素，交换并更新基准索引（向前遍历，前大后小则交换）
4.重复步骤2，3直到首尾重合
5.对基准索引前和后的两个序列分别指向步骤1 2 3 4

最坏时间复杂度：O（n^2）
最优时间复杂度：O（nlogn）
稳定性：不稳定

def quick_sort(li,start,end):
 if start >= end:
     return
 #  确定基准索引
 pivot_index = (start +end) //2
 head = start
 tail = end
 while head <tail:
 #  在基准索引前找比基准值大的元素，交换并更新基准索引 （向后遍历，前大后小则交换）
      while head < pivot_index and li[head] <= li[pivot_index]:
         head += 1
      li[head],li[pivot_index] = li[pivot_index],li[head]
      pivot_index = head
 #  在基准索引后找比基准值小的元素，交换并更新基准索引（向前遍历，前大后小则交换）
      while tail > pivot_index and li[tail] >= li[pivot_index]:
           tail -= 1
      li[tail],li[pivot_index] = li[pivot_index],li[tail]
      pivot_index = tail
 #  重复步骤2，3直到首尾重合
 #  对基准索引前和后的两个序列分别指向步骤1
 # 至此，原序列被分割成里li[start:pivot_index] 和li[privot_index:end]
 quick_sort(li,start,pivot_index-1)
 quick_sort(li,pivot_index+1,end)
if __name__ == '__main__':
  li = [5,6,8,9,3,1,6,7]
  quick_sort(li,0,len(li)-1)
  print(li)

归并排序：
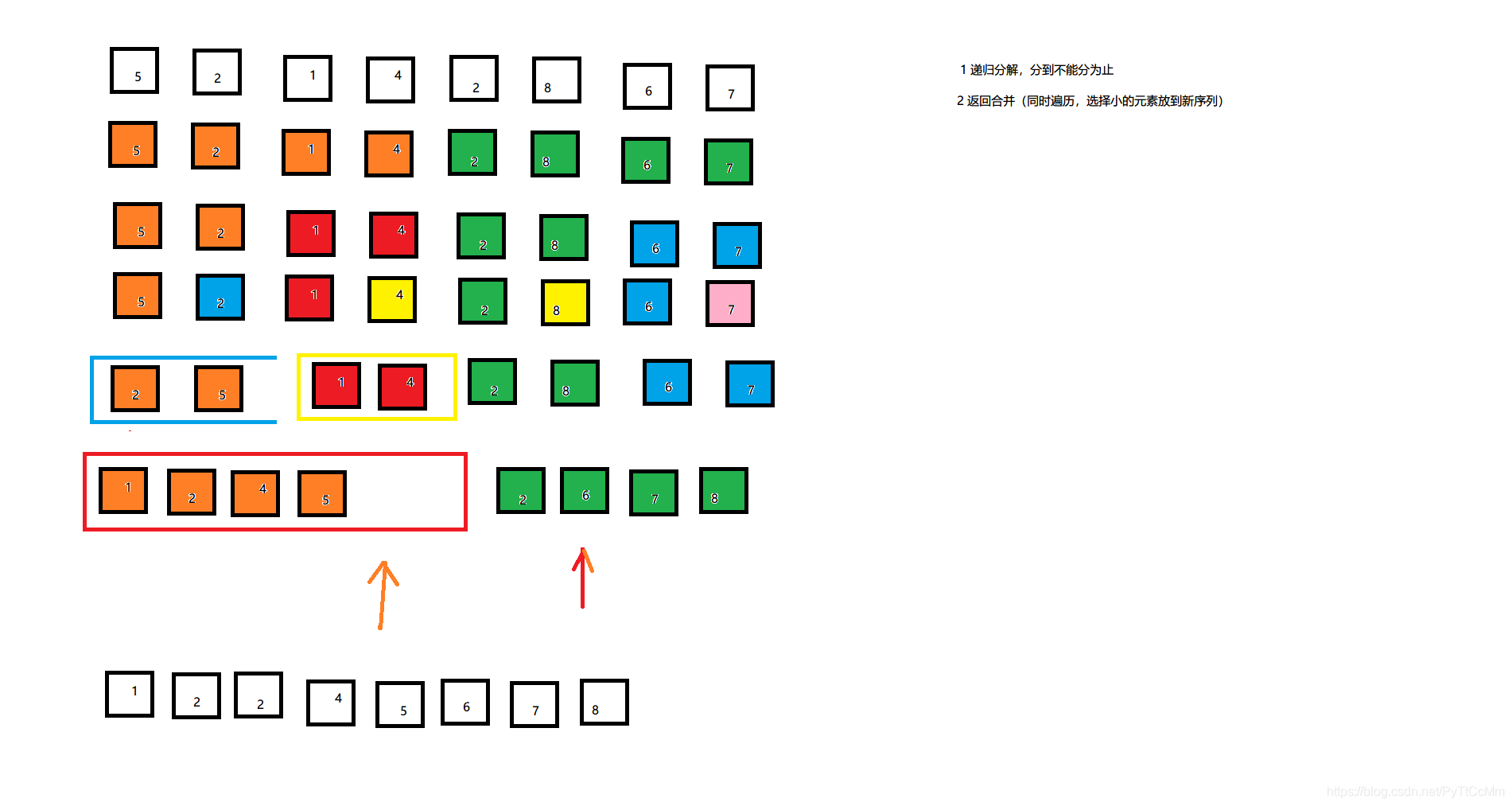
1.递归分解，分到不能分为止
2.返回归并（同时遍历，选择晓得元素放到新序列）
时间复杂度： O（nlogn）
稳定性：稳定

def merge_sort(li):
  n = len(li)
  if n <= 1:
      return
  # 递归分解，分到不能分为止
  left = li[0:n//2]
  right = li[n//2 :n]
  # 继续调用，继续分
  merge_sort(left)
  merge_sort(right)

  # 返回合并（将左右序列合并到原始序列中）
  li[:]= []
  # 同时遍历，选择小的元素放到新序列
  l_index = 0
  r_index = 0
  # 此时左半部分有序，右半部分有序
  while l_index < len(left) and r_index < len(right):
      if left[l_index] <= right[r_index]:
           li.append(left[l_index])
           l_index += 1
      else:
          li.append(right[r_index])
          r_index += 1
  # 至此，左右其中之一遍历完成，江另一部分所有严肃放入列表
  li += left[l_index:]
  li += right[r_index:]

if __name__ == '__main__':
  li = [5,8,3,9,1,2,9,7,6]
  merge_sort(li)
  print(li)