1.离散型随机变量
E(X)=∑i=1nxipiE(X)=\sum_{i=1}^{n}x_ip_iE(X)=i=1∑nxipi
D(X)=σ2=E(X2)−[E(X)]2D(X)=\sigma^2=E(X^2)-[E(X)]^2D(X)=σ2=E(X2)−[E(X)]2
1.1 二项分布
- nnn个相同试验;
- 每次试验只有2个可能的结果;
- 出现“成功”的概率ppp对每一次试验是相同的;
- 试验相互独立;
- 试验“成功”或“失败”可以计数;
E(X)=npE(X)=npE(X)=np
D(X)=npqD(X)=npqD(X)=npq- n=1n=1n=1时,P{X=x}=pxq1−xP\{X=x\}=p^xq^{1-x}P{X=x}=pxq1−x,x=0,1x=0,1x=0,1,即0−10-10−1分布。
1.2 泊松分布
描述在一指定时间范围内或在指定的面积或体积内某一时间出现的次数的分布。
P(X)=λxe−λx!,x=0,1,2,...P(X)=\frac{\lambda^xe^{-\lambda}}{x!},x=0,1,2,...P(X)=x!λxe−λ,x=0,1,2,...
λ\lambdaλ为给定时间间隔内时间的平均数。
E(X)=D(X)=λE(X)=D(X)=\lambdaE(X)=D(X)=λ
2. 连续型随机变量
P(a<X<b)=∫abf(x)dxP(a<X<b)=\int_a^bf(x)dxP(a<X<b)=∫abf(x)dx
满足f(x)>0f(x)>0f(x)>0,∫−∞∞f(x)=1\int_{-\infty}^{\infty}f(x)=1∫−∞∞f(x)=1。
E(X)=∫−∞∞xf(x)dx=μE(X)=\int_{-\infty}^{\infty}xf(x)dx=\muE(X)=∫−∞∞xf(x)dx=μ
D(X)=∫−∞∞[x−E(X)]2f(x)dx=σ2D(X)=\int_{-\infty}^{\infty}[x-E(X)]^2f(x)dx=\sigma^2D(X)=∫−∞∞[x−E(X)]2f(x)dx=σ2
2.1 正态分布
f(x)=1σ2πe−12σ2(x−μ)2,−∞<x<∞f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2},-\infty<x<\inftyf(x)=σ2π1e−2σ21(x−μ)2,−∞<x<∞
记作X∼N(μ,σ2)X\sim N(\mu,\sigma^2)X∼N(μ,σ2)。
转化成标准正态分布Z=X−μσ∼N(0,1)Z=\frac{X-\mu}{\sigma}\sim N(0,1)Z=σX−μ∼N(0,1)。
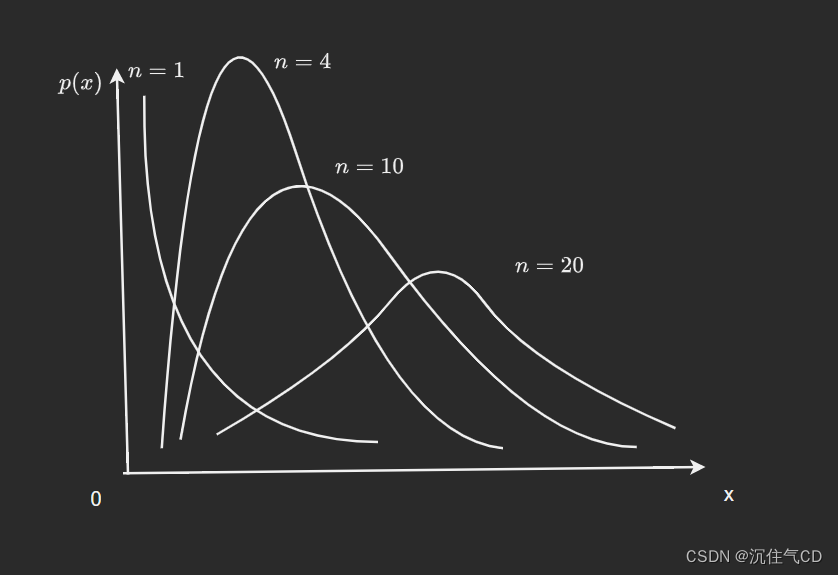
2.2 χ2\chi^2χ2分布
- 设随机变量X1,X2,...,XnX_1,X_2,...,X_nX1,X2,...,Xn相互独立,且Xi(i=1,2,...,n)X_i(i=1,2,...,n)Xi(i=1,2,...,n)服从标准正态分布N(0,1)N(0,1)N(0,1),则它们的平方和∑i=1nXi2\sum_{i=1}^{n}X_i^2∑i=1nXi2服从自由度为nnn的χ2\chi^2χ2分布。
- 自由度nnn——独立变量的个数。
- E(χ2)=nE(\chi^2)=nE(χ2)=n;D(χ2)=2nD(\chi^2)=2nD(χ2)=2n。
- 分布可加性χ12+χ22=χ2(n1+n2)\chi_1^2+\chi_2^2=\chi^2(n_1+n_2)χ12+χ22=χ2(n1+n2)
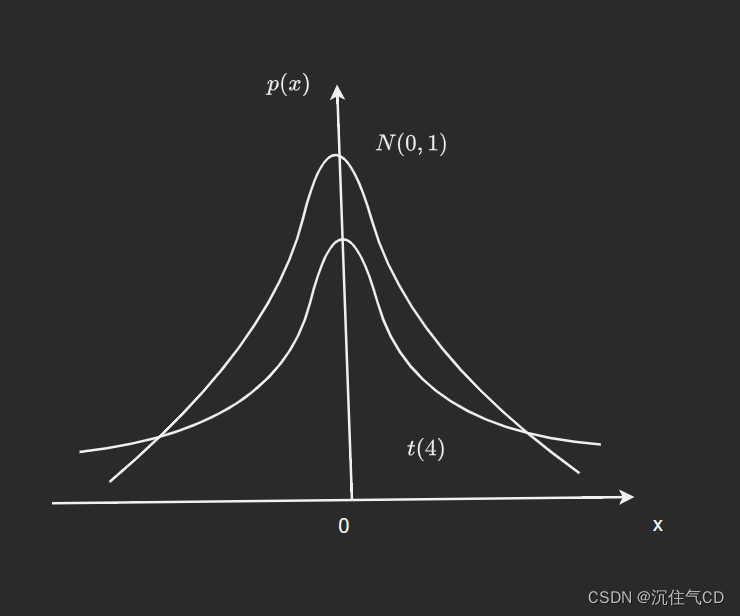
2.3 ttt分布
- 设随机变量X∼N(0,1)X\sim N(0,1)X∼N(0,1),Y∼χ2(n)Y\sim \chi^2(n)Y∼χ2(n),且XXX与YYY独立,则
t=XY/nt=\frac{X}{\sqrt {Y/n}}t=Y/nX
记为t(n)t(n)t(n),nnn为自由度。- n≥2n\ge 2n≥2时,ttt分布的数学期望E(t)=0E(t)=0E(t)=0;
- n≥3n\ge 3n≥3时,D(t)=nn−2D(t)=\frac{n}{n-2}D(t)=n−2n;
- n=1n=1n=1时,为柯西分布;
- n≥30n\ge 30n≥30时,无限接近N(0,1)N(0,1)N(0,1)。
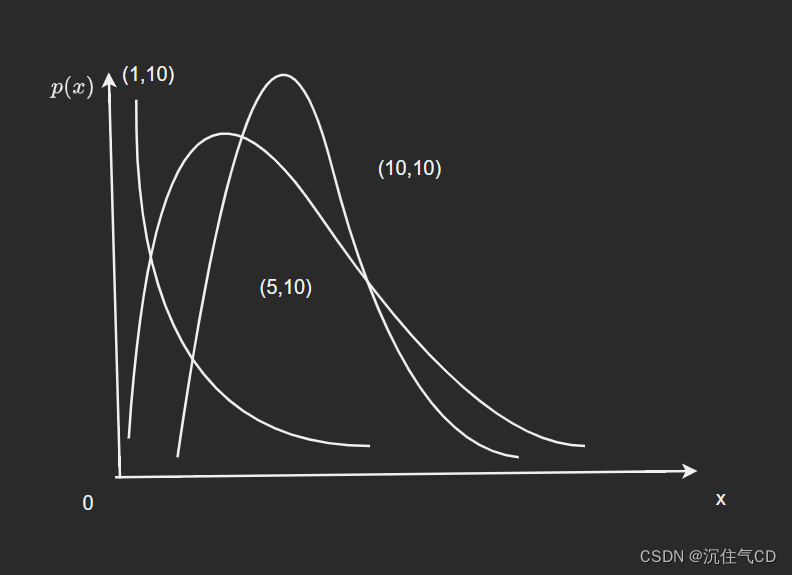
2.4 FFF分布
- 设随机变量YYY与ZZZ相互独立,且YYY和ZZZ分别服从自由度为mmm和nnn的χ2\chi^2χ2分布。
X=Y/mZ/n=mYmZX=\frac{Y/m}{Z/n}=\frac{mY}{mZ}X=Z/nY/m=mZmY
称XXX服从第一自由度为mmm,第二自由度为nnn的FFF分布,记为F(m,n)F(m,n)F(m,n)。
E(X)=nn−2,n>2E(X)=\frac{n}{n-2},n>2E(X)=n−2n,n>2
D(X)=2n2(m+n−2)m(n−2)(n−4),n>4D(X)=\frac{2n^2(m+n-2)}{m(n-2)(n-4)},n>4D(X)=m(n−2)(n−4)2n2(m+n−2),n>4





 本文概述了离散型随机变量(如二项分布和泊松分布)以及连续型随机变量(如正态分布、χ2分布、t分布和F分布)的基本概念、期望和方差计算。介绍了这些分布在实际问题中的应用,特别是对于概率论和统计分析的重要性。
本文概述了离散型随机变量(如二项分布和泊松分布)以及连续型随机变量(如正态分布、χ2分布、t分布和F分布)的基本概念、期望和方差计算。介绍了这些分布在实际问题中的应用,特别是对于概率论和统计分析的重要性。
















 6684
6684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








