文章目录
1 基本信息
| 项目 | 信息 |
|---|---|
| 名称 | Matrix factorization techniques for recommender systems |
| 作者 | Yehuda Koren, Robert Bell, Chris Volinsky |
| 期刊 | Computer |
| 年份 | 2009 |
| 卷 | 42 |
| 期 | 8 |
| 页码 | 30–37 |
| DOI | https://doi.org/10.1109/MC.2009.263 |
| 引用量 | 10063 |
2 引言
正如 Netflix 奖竞赛所证明的那样,矩阵分解模型在生成产品推荐方面优于经典的最近邻技术,允许结合其他信息,例如隐式反馈、时间效应和置信度。
推荐系统的目标是使得不同的用户都尽可能得到满足,也即是个性化推荐,使得服务提供者获取用户的满意度和忠诚度。
3 推荐系统策略
从广义上讲,推荐系统基于两种策略之一。
- 内容过滤(content filtering) 方法为每个用户或产品创建一个画像(配置文件)以表征其性质。
- 协同过滤(collaborative filtering) 方法分析用户之间的关系和产品之间的相互依赖关系,以识别新的用户-项目关联。
协同过滤相比内容过滤,有两点优势:
- 不需要刻画画像,应用更广泛。
- 通常更准确。
协同过滤相比内容过滤,有一点劣势:
- 遭遇冷启动问题。
协同过滤的两个主要领域是邻域方法(neighborhood methods) 和潜在因子模型(latent factor models)。
- 邻域方法的中心是计算项目之间或用户之间的关系。
- 潜在因素模型是一种替代方法,它试图通过对项目和用户进行表征,例如从评分模式推断出的 20 到 100 个因素来解释评分。
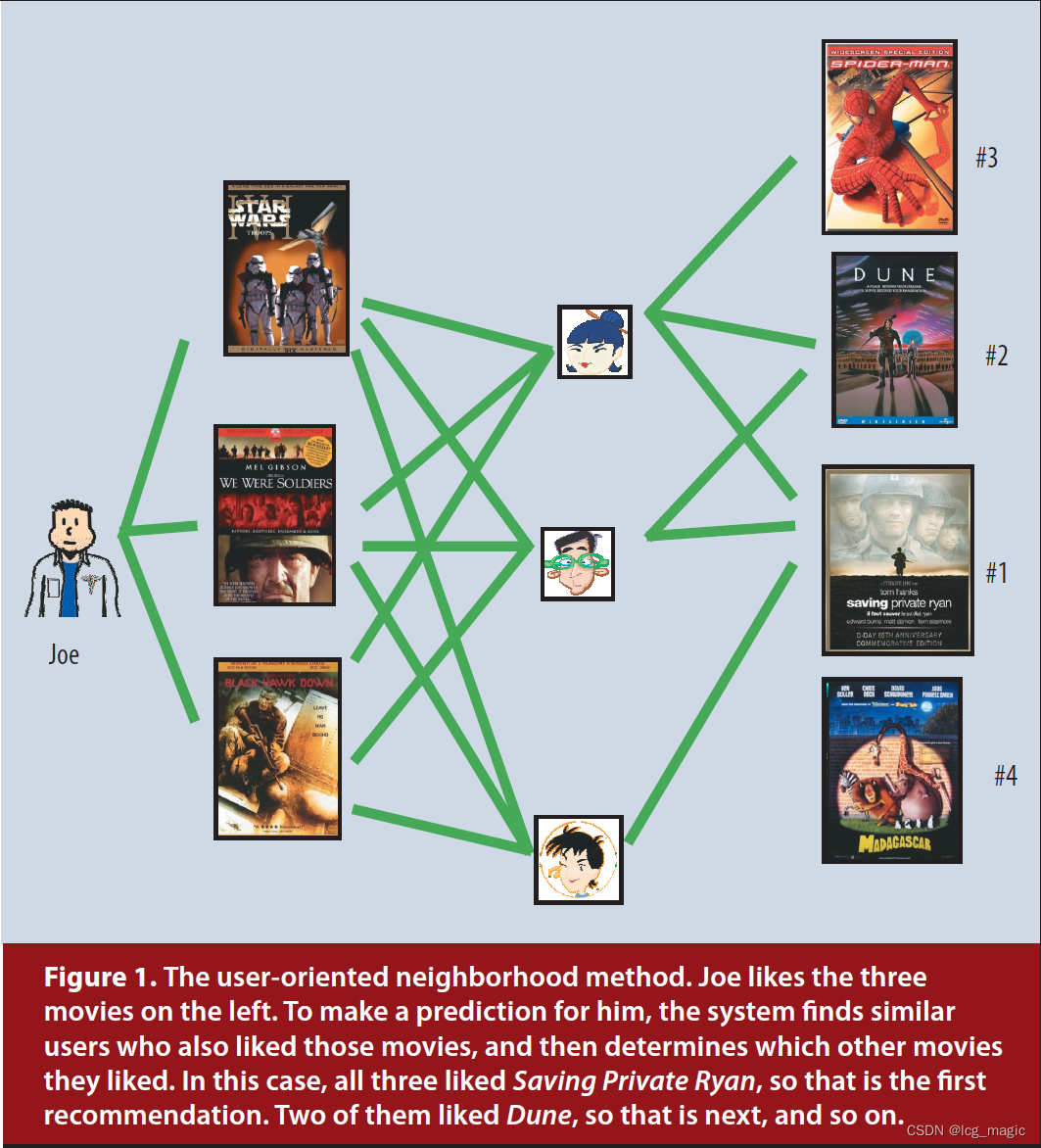
图 1 展示了面向用户的邻域方法。Joe 喜欢最左侧的 3 部电影。为了给 Joe 做预测,系统先找到同样喜欢这些电影的 3 个用户(中间)。那么如何向 Joe 推荐(预测)呢?这 3 个用户都喜欢 Saving Private Ryan 这部电影,那么最建议推荐就是它。其次,有两个用户喜欢 Dune,那么这个是第二推荐的。以此类推。
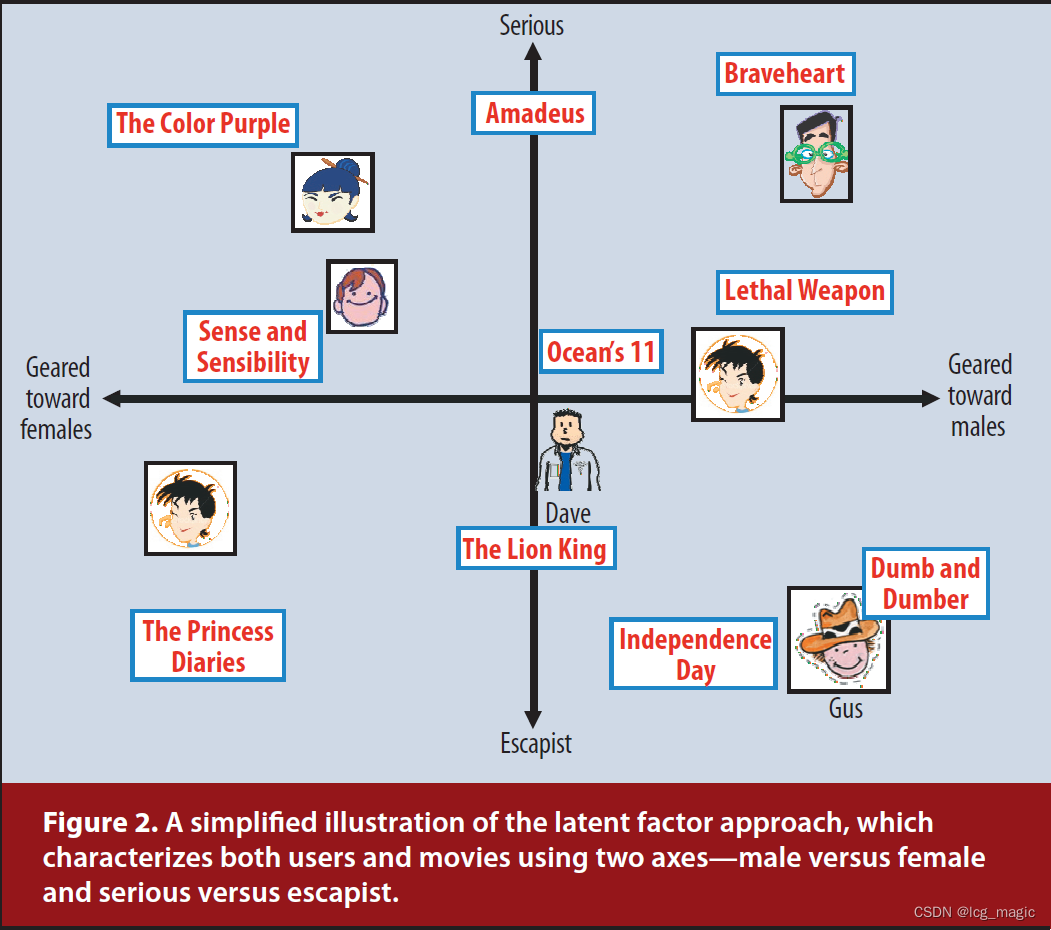
图 2 展示了潜在因子方法在 2 维下的一个简化例子。考虑两个假设维度,即女性(左)与男性(右)导向以及严肃(上)与逃避现实(下)。该图显示了几部知名电影和少数虚构用户可能落在这两个维度上的位置。对于这个模型,用户对电影的预测评分,相对于电影的平均评分,将等于电影和用户在图表上的位置的点积。例如,我们希望 Gus 喜欢 Dumb and Dumber,讨厌 The Color Purple,并对Braveheart 评分一般。
4 矩阵分解方法
潜在因子模型的一些最成功的实现是基于矩阵分解(Matrix Factorization)。在其基本形式中,矩阵分解通过从项目评分模式推断出的因子向量来表征项目和用户。项目和用户因子之间的高度对应导致推荐。
推荐系统依赖不同类型的输入数据,通常表示为一个矩阵,矩阵的一个维度表示用户,另外一个维度表示感兴趣的项目。最方便的数据是高质量的显式反馈,其中包括用户关于他们对产品的兴趣的明确输入。文中以评分(ratings) 作为显式用户反馈。通常,显式反馈包含一个稀疏矩阵,因为任意单一用户可能只对一小部分可能的项目进行了评分。
矩阵分解的一个优点是它允许合并额外的信息。当显式反馈不可用时,推荐系统可以使用隐式反馈推断用户偏好,隐式反馈通过观察用户行为间接反映意见,包括购买历史、浏览历史、搜索模式,甚至鼠标移动。 隐式反馈通常表示事件的存在或不存在,因此它通常由一个密集填充的矩阵表示。
5 基本矩阵分解模型
符号表如下所示
| 符号 | 含义 |
|---|---|
| f f f | 联合潜在因子空间维度 |
| i i i | 项目 |
| q i ∈ R f q_i \in \mathbb{R}^f qi∈Rf | 和 i i i 相关联的向量 |
| u u u | 用户 |
| p u ∈ R f p_u \in \mathbb{R}^f pu∈Rf | 和 u u u 相关联的变量 |
| r u i r_{ui} rui | 用户 u u u 对项目 i i i 的评分 |
对于给定的项目 i i i, q i q_i qi 的元素衡量该项目拥有这些因素的程度,无论是积极的还是消极的。
对于给定的用户 u u u, p u p_u pu 的元素衡量用户对相应因素高的项目的兴趣程度,同样,积极或消极。
结果的点积 q i T p u q^{\rm{T}}_i p_u qiTpu 捕获了用户 u u u 和项目 i i i 之间的交互——用户对项目特征的整体兴趣。
u u u 对 i i i 评分的一个估计:
r ^ u i = q i T p u . (1) \qquad \qquad \qquad \hat{r}_{ui}=q^{\rm{T}}_i p_u. \qquad \qquad \qquad \textbf{(1)} r^ui=qiTpu.(1)
这种模型与奇异值分解 (SVD) 密切相关,奇异值分解是一种在信息检索中识别潜在语义因素的成熟技术。在协同过滤域中应用 SVD 需要考虑用户项目评分矩阵。由于用户项目评分矩阵中的稀疏性导致缺失值的比例很高,这通常会带来困难。
为了学习因子向量( p u p_u pu 和 q i q_i qi),系统最小化一组已知评分的正则化平方误差:
min q ∗ , p ∗ ∑ ( u , i ) ∈ κ ( r u i − q i T p u ) 2 + λ ( ∥ q i ∥ 2 + ∥ p u ∥ 2 ) , (2) \min_{q^{\ast}, p^{\ast}} \sum_{(u,i) \in \kappa} \left( r_{ui} - q^{\rm{T}}_i p_u \right)^2 + \lambda \left( \Vert q_i \Vert^2 + \Vert p_u \Vert^2 \right), \qquad \textbf{(2)} q∗,p∗min(u,i)∈κ∑(rui−qiTpu)2+λ(∥qi∥2+∥pu∥2),(2)其中 κ \kappa κ 是已知 r u i r_{ui} rui 的(训练集) ( u , i ) (u,i) (u,i) 对的集合。常数 λ \lambda λ 控制正则化的程度,通常由交叉验证确定。
个 人 理 解 : {\color{Orange}个人理解:} 个人理解:
真实评分 r u i r_{ui} rui,预测评分 q i T p u q^{\rm{T}}_i p_u qiTpu,两者误差为 ( r u i − q i T p u ) (r_{ui} - q^{\rm{T}}_i p_u) (rui−qiTp





 本文探讨了矩阵分解技术在推荐系统中的核心作用,从Netflix大奖赛案例出发,介绍了矩阵分解模型、学习算法(随机梯度下降与交替最小二乘)、加入偏差、额外输入源(如隐式反馈和用户属性)、时间动态以及处理不同置信度的评分。关键概念包括协同过滤、潜在因子模型和SVD,展示了如何通过这些方法提高个性化推荐的准确性。
本文探讨了矩阵分解技术在推荐系统中的核心作用,从Netflix大奖赛案例出发,介绍了矩阵分解模型、学习算法(随机梯度下降与交替最小二乘)、加入偏差、额外输入源(如隐式反馈和用户属性)、时间动态以及处理不同置信度的评分。关键概念包括协同过滤、潜在因子模型和SVD,展示了如何通过这些方法提高个性化推荐的准确性。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 948
948

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








