算法学习（11）数学问题求解系列（8）素数求解（多种方法比较）（结尾有彩蛋~）

前言

这段时间，开始入门学习Python科学计算，关于算法的学习受到影响……不过在准备这篇博客的时候，我发现算法学习，始终是编程学习中最重要的一环。因为算法的程序实现过程中，特别考验我们对手中编程语言的理解，“明明实现一样功能的语句，为什么有些运行起来快，有些运行起来慢呢？”。在实现算法的过程中，我们会不停遇到这些问题，而当我们能自己回答这些问题的时候，我们才真正有底气声称自己掌握了某门语言。而学习Python科学计算的过程，我感觉更像是在操作一个工具，少了探究程序运行效率的乐趣……（觉得文章太长，一定记得看文章后面的彩蛋……）

问题

找出10万以内的素数

名词解释

素数，也叫质数，就是因子只有1和它本身，如$2,3,5,17$等。合数，大于2，且不属于质数的整数。

编程思路

1. 给定一个数$a$, 依次除以 $2$ 到 $Sqrt(a)+1$ （只需要除到 $\sqrt{a}+1$ 的原因见之前亲密数或是完数的求解 传送门）
2. 如果发现了能整除数 $a$ 的因子，即可退出循环
3. 等排除掉所有合数，剩下的就是质数。

实现代码

def findPrimeNum(maxLimit):
    primeNunList = [1]*maxLimit  # 创建与待研究范围一样的数组; 一开始假设都是，因为排除合数比挑出素数简单，排除只需要一个整除即可！
    for num in range(2, maxLimit):  # 全部数都要遍历一遍
        for j in range(2, int(math.sqrt(num)) + 1):  # 一定要从2开始！
            if num % j == 0:  # 说明整除
                primeNunList[num] = 0  # 标为合数，剩下的就是
                break  # 有一个即可
    for i in range(2, maxLimit):
        if primeNunList[i] == 1:
            print(i)

运行效果

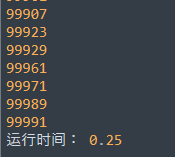
代码分析

1. 建立数组 primeNunList = [1]*maxLimit, 数组的长度等于我们要搜寻的数的范围，研究10万内的数，数组的长度就是10万（对于现代计算机，这个开销是可以承受的）
2. 每个数作为数组的索引，每个位置存储$0$ 或 $1$, $1$ 表示对应的数为质数，如 primeNumList[3] = 1
3. 之后依次除以因子，发现有整除的，更新该位置的值为0（表明为合数），然后即可跳出内层循环。

性能分析

这个算法很直观，于是，缺点也很明显，比如，素数肯定都是奇数(2除外)，对吧？但程序还是对偶数一视同仁考虑进去，同理，如果3的倍数，5的倍数，7的倍数，是不是也要排除呢？对于确定合数，我们只需要知道它一个因子就好，于是，上面说的倍数，依次排除掉，到最后不就只剩下素数了吗？(小问题，为什么这段文字里，我不说4的倍数和6的倍数排除掉？)

更强的算法

基于上一段文字的分析，在素数这里有个Eratosthenes算法，它的思路就是，依次排除素数的倍数，剩下的就都是素数了。

编程思路

1. 对于10万范围内的整数，候选的因子是 $2$ 到 $\sqrt{10万}+1$
2. 从第一个因子开始，把它的所有倍数排除掉，比如一开始因子是2，则第一遍下来，所有偶数就排除了（于是4和6，及它们的倍数，就都没了，这是上面问题的答案，你想明白了吗？）
3. 接下来是 $3,5,7...$的倍数（剩下来的因子都是质数）

实现代码

def findPrimeNum3(maxLimit):  # 在教材的方法上改进
    primeNunList = [1]*maxLimit
    for i in range(2, int(math.sqrt(maxLimit))+1):  # 这是除数，从2开始，最多到 sqrt(maxLimit)就能判断最后一个数了
        if primeNunList[i] == 0:
            continue
        for j in range(2*i, maxLimit, i):  # 步长设为 i!!!
            if j % i == 0:  # 说明 j 是合数
                primeNunList[j] = 0
                # break  这里不能使用break,因为这个循环就是要排除所有 i 的倍数
    for i in range(2, maxLimit):
        if primeNunList[i] == 1:
            print(i)

运行效果

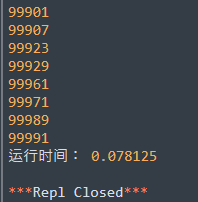
是不是效果立竿见影！！！

代码分析

1. if primeNunList[i] == 0: continue，因为所有的数字是存储在一起的，已经在之前被排除的数，还是会被考虑进来，于是，通过判断该值是$0$(合数)或是$1$ (素数) 来决定要不要用来当除数。这里 continue语法是，如果是合数，就直接跳到下一个数
2. 整个算法的核心是这一句：for j in range(2*i, maxLimit, i): # 步长设为 i!!!， 既然我们要排除的是因子 i 的倍数，那更新的步长，不正是每次加 i 吗？！(之后会列举教材的错误解法，完全毁掉了整个算法……)
3. 思考下，为什么在 $j$ 的循环里，不能使用break？
4. 上述程序还有一个bug，拖慢了程序运行，你发现了吗？（在这里致谢我的舍友，他对我写的博客很好奇，然后在跟他讨论的过程中，我意识到这个bug~果然学习要多跟人交流）

反面例子分析

在学习算法的过程中，我们确实要多看多模仿正确高效的代码实现，但是，反面的例子也要多研究分析，如果能独立分析反面例子出错的地方，或是效率低下的地方，这对加深我们对手头编程语言的理解，大有裨益。认识坑在哪，才不会掉坑，对吧？

错误例子一：选除数没有排除合数

低效代码

def findPrimeNum2(maxLimit):  # 使用Eratosthenes算法
    primeNunList = [1]*maxLimit
    for i in range(2, int(math.sqrt(maxLimit))+1):  # 这是除数，从2开始，最多到 sqrt(maxLimit)就能判断最后一个数了
        for j in range(2*i, maxLimit):  # 这里还可以增加一个判断，已经确定是合数就跳过！ 于是，这里的步长设为 i不就可以了！
            if j % i == 0:  # 说明 j 是合数
                primeNunList[j] = 0
                # break  这里不能使用break,因为这个循环就是要排除所有 i 的倍数
    for i in range(2, maxLimit):
        if primeNunList[i] == 1:
            print(i)

运行效果

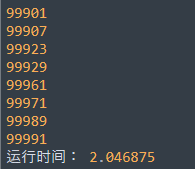
是的，速度比普通方法还慢,然后，我写的……对着教材都打错

出错分析

1. 在第一个for循环，for i in range(2, int(math.sqrt(maxLimit))+1):, 这里是选除数的地方，Eratosthenes算法高效的地方在于选出质数当除数，而我这里没有增加素数的判断，把合数也算进去，怎么可能不慢……

错误例子二 （教材的方法）

低效代码

def findPrimeNum2(maxLimit):  # 使用Eratosthenes算法
    primeNunList = [1]*maxLimit
    for i in range(2, int(math.sqrt(maxLimit))+1):  # 这是除数，从2开始，最多到 sqrt(maxLimit)就能判断最后一个数了
        if primeNunList[i] == 0:  # 素数采用做除数
            continue
        for j in range(2*i, maxLimit):  # 这里还可以增加一个判断，已经确定是合数就跳过！ 于是，这里的步长设为 i不就可以了！
            if j % i == 0:  # 说明 j 是合数
                primeNunList[j] = 0
                # break  这里不能使用break,因为这个循环就是要排除所有 i 的倍数
    for i in range(2, maxLimit):
        if primeNunList[i] == 1:
            print(i)

运行效果

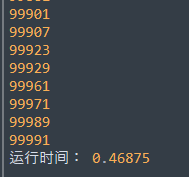
你没看错，这就是教材标榜的高效算法，怎么比普通算法还慢……

出错分析

1. 这里问题出在第二个 for 循环， for j in range(2*i, maxLimit): # 于是，这里的步长设为 i不就可以了！, 我在注释已经写出来了改正方法，既然这个算法的核心是按质数的倍数剔除合数，for这里的步长设为1，是闹哪样？

错误例子三 （搞笑的我以为）

低效的代码

def findPrimeNum3(maxLimit):  # 在教材的方法上改进
    primeNunList = [1]*maxLimit
    for i in range(2, int(math.sqrt(maxLimit))+1):  # 这是除数，从2开始，最多到 sqrt(maxLimit)就能判断最后一个数了
        if primeNunList[i] == 0:
            continue
        for j in range(2*i, maxLimit):  # 这里还可以增加一个判断，已经确定是合数就跳过！ 于是，这里的步长设为 i不就可以了！
            if primeNunList[j] == 0:  # 进来说明j已经被筛过了
                continue
            if j % i == 0:  # 说明 j 是合数
                primeNunList[j] = 0
                # break  这里不能使用break,因为这个循环就是要排除所有 i 的倍数
    for i in range(2, maxLimit):
        if primeNunList[i] == 1:
            print(i)

运行效果

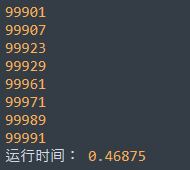
没有任何提升和改善，对比上个程序，你们看出我改了哪里吗……

低效分析

for j in range(2*i, maxLimit):  # 这里还可以增加一个判断，已经确定是合数就跳过！ 
            if primeNunList[j] == 0:  # 进来说明j已经被筛过了
                continue

1. 上面是变动的地方，我觉得，既然后面还需要判断 $j$ 是不是合数，为什么不提前判断，这样可以少循环一些数……（我现在还不知道当时脑子里在想什么）
2. 这里运行时间没有变，说明
   1） 程序计时程序很准
   2) 我所谓的改善，没有拖慢也没有提升程序……我不过是把下面的 if 判断，提到上面，根本没有任何实质性改变……所以，我这里只是增加了代码行数，

总结

综合比较

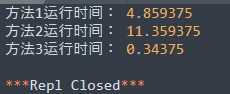
上面介绍的方法，由于实验对象是10万，运行效率差异还不是那么震撼。这里，我把每个函数的 print 语句去掉，然后数字增加到100万。 方法1是常规方法，方法2是教材的方法（错误例子二），方法三是我正确运用算法的例子，于是这里也体现了一个好的算法的重要性。

零散经验总结

1. 重点理解为什么预先假设全为素数，因为排除合数简单，只要有一个因子，就可以不用再除；而素数，是要统计，确保没有一个因子，才能退出，程序实现会更麻烦
2. 用预先一个大数组，是为了方便有筛子法，对于第一个方法，其实无所谓预先建立一个大数组
3. 这些练习的价值：因为结果简单，更容易让我们发现每一个语句如何影响程序的运行，就像口语练习，从最简单的句子，更好模仿语音语调
4. 因此，改善程序的时候，最后一次改一步，这样才知道那些改动是有价值的
5. 编写成一个函数运行，会比直接写脚本快……具体原因我不知道，这得看编译原理这些的书吧……同样的程序，我包装成函数运行，速度是0.17秒（100万规模），写成脚本，就是.0.25秒……
6. 用for循环去建立数组，会很慢……最好也是用内置赋初值的方式；同时使用数组前，预定义大小会比调用append() 快。速度比较看下图
   
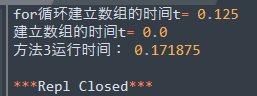
   下面代码，在程序中一定要避免，建数组最慢的方式都用上了……

for i in range(maxLimit):
        testArray2.append(1)

推荐使用,运行时间用秒是忽略不计的

testArray2 = [1]*maxLimit

彩蛋

这篇博客真的太长了……不知道有多少人能看到这，看到这就是真爱了~ 其实，上面列举的程序，都不是最高效的，真正的程序在这！上面更强算法，是有瑕疵的。

实现代码

def findPrimeNum3(maxLimit):  # 在教材的方法上改进
    primeNunList = [1]*maxLimit
    for i in range(2, int(math.sqrt(maxLimit))+1):  # 这是除数，从2开始，最多到 sqrt(maxLimit)就能判断最后一个数了
        if primeNunList[i] == 0:
            continue
        for j in range(2*i, maxLimit, i):  # 步长设为 i!!!
            # if j % i == 0:  # 说明 j 是合数， 这个判断是多余的……这是人家的倍数啊……
            primeNunList[j] = 0

运行效果

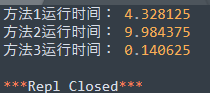
你没看错，真正运行完，只需要$0.14s$， 而不是上面的 $0.34s$。

代码分析

1. 唯一的改变，注释已经给了理由，在第二个 for 循环里。

for j in range(2*i, maxLimit, i):  # 步长设为 i!!!
            # if j % i == 0:  # 说明 j 是合数， 这个判断是多余的……这是人家的倍数啊……

小总结

这里告诉我们，if 语句对程序的影响很大，足足增加了 $0.2s$， 所以编写程序过程中，能减少判断减少判断。