算法学习（2）常用排序算法合集

前言

这篇博客会先介绍几种常用的排序算法，对于简单的，只会给出代码，不会有过多解释。之后，所有程序会引入计时部分，比较各类排序算法的速度。

常用算法

冒泡法

特点

相邻两两比较，这里面最需要注意的是，如果希望从前往后排好序，扫描的循环，必须从后面开始，这样是为了，每一遍扫描，可以把未排序部分里面最小的元素调出来，然后跟要排好序的位置比（内循环有种预选赛的感觉，大家对着代码，可以试试内循环从前面开始，会出现什么有趣现象，我是掉坑里的了……）

实现代码

# 冒泡法的核心，是每一遍遍历，把最小的数上浮，比较的是相邻的元素，到了最后一步，把后面挑选出来的最小值跟待排的位置比，完成前面的排序
def BubleSort(array):
    n = len(array)
    print('排序前：', array)
    for i in range(n):
        for j in range(n-1, i, -1):
            if array[j] < array[j-1]:
                array[j], array[j-1] = array[j-1], array[j]
        # 一个j遍历结束，一个大数就往后沉
        print('第', i+1, '次：', array)


myArray = [0]*10
isCreated = CreateRandomNumber.CreateRandomNumer(10, myArray, 1, 100)  # 固定产生10个1到100件的随机数
if isCreated:
    BubleSort(myArray)

注：CreaterandomNumber(array_length, array, min, max)是产生随机数的程序，在排序法的准备里面提及。

运行效果

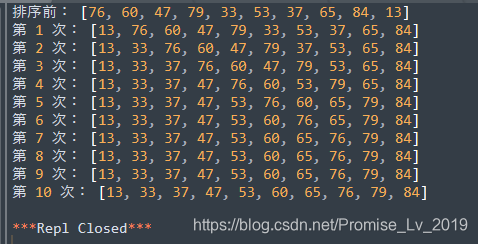
缺点

大家注意下排序次数，不管数组有没有排好序，数组多长，就会扫描多少遍，如果数组本来是有序的，或基本有序，这个算法就显得很笨。

优化的冒泡法

特点

相邻两两排序
智能判断序列是否有序： 针对普通冒泡法的改进，如果在一次扫描过程，没有任何一次交换，就说明数组已经有序，不需要循环了。

实现代码

# 冒泡法的核心，是每一遍遍历，把最小的数上浮，比较的是相邻的元素，到了最后一步，把后面挑选出来的最小值跟待排的位置比，完成前面的排序
def BubleSort(array):
    n = len(array)
    print('排序前：', array)
    for i in range(n):
        isInOrder = True  # 假设数组有序，因为只要有一次交换，自然会被更改
        for j in range(n-1, i, -1):
            if array[j] < array[j-1]:
                array[j], array[j-1] = array[j-1], array[j]
                isInOrder = False  # 在j的循环里面，只要发生一次交换，就说明数组不是有序的
        # 一个j遍历结束，一个大数就往后沉
        print('第', i+1, '次：', array)
        if isInOrder:
            break

更改的代码，已经在上图中，下面简单罗列下：

1. 在每个i循环前，设置一个 isInOrder = True
2. 如果在内层循环j 中，有发生数字交换，说明没排好，isInOrder = False
3. 如果没有交换，到了后面就会提前跳出 外层循环

运行效果：

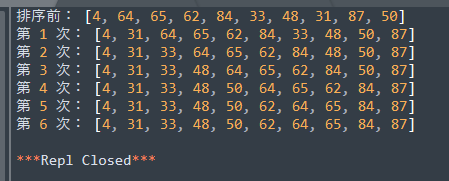
依然是10个数待排，不过因为数组不是太乱，所有用了5次就排完，第6次相当于校验。这在数字多的时候，能极大提高效率。

缺点

暂时还没发现。

快速排序法

特点

快排也是冒泡排序法的改进，不同的是，快排使用分治的思想 ，把数组不断细分，左边小于右边的两个数组，中间这个数，在这个过程就是排好的。细分到每个部分为空或是1个元素，这个大数组就排好了。

鉴于快排不是很好理解，代码里面有详细的说明，建议大家复制代码，放到Sublime Text 这些有语法高亮的编辑器里面，容易阅读。

实现代码

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date    : 2019-03-24 21:55:57
# @Author  : Promise (promise@mail.ustc.edu.cn)
# @Link    : ${link}
# @Version : $Id$
import CreateRandomArray


# 快排排序有两个部分，一个是分割（排序的关键),另一个是不断自我调用的递归函数
def Division(array, left, right):
	base = array[left]  # 统一约定
	while left < right:  # 最重要的边界条件
		while array[right] > base and left < right:  # 从右边开始, 我遗漏了个重要条件，left right要一直比较
			right -= 1
		# 跳出循环后，就找到了右边比base小的第一个元素
		array[left] = array[right]  # 这时，array[left]的值在base里面，没有丢		
		while array[left] < base and left < right:
			left = left + 1
		# 跳出循环后，就找到了左边比base大的元素
		array[right] = array[left]  # 上一步，array[right]的值挪走了，这时候可以放一个比base的值进来	
	array[left] = base  # 跳出大循环后，说明left的指标 >= right, 于是找到了中点这时base 放这里刚刚好
	print(array)
	return left  # left位置上的数，就是排好序的

def quickSort(array, left, right):
	if left < right:
		middle = Division(array, left, right)  # 找到中点，于是数组可以分成两个子数组
		print(middle)
		# 递归调用
		quickSort(array, left, middle-1)  # i这个位置是排好序的，不能再算进去
		quickSort(array, middle+1, right)
	# 至此，完成排序

运行效果

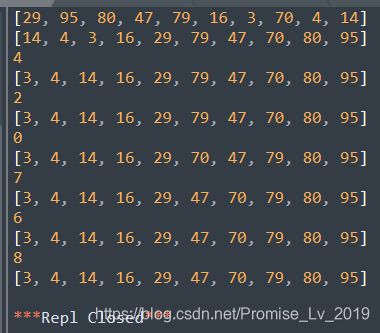
因为QuickSort函数里面运用了递归调用，所以每一次的追溯并不直观。输出的单独数字，是每次运行该程序，输出的中间位置的索引，上式说明函数递归调用了6次。

特别强调

1. 对于快排算法的两个函数，核心是第一个划分数组的函数，每次输出的中点位置，就是原数组第一个元素应该待的位置，也就是，每分一次数组，子数组的第一个元素就排好。
2. 这个函数容易出错的地方，在于left 和 right 两个参数的不断内缩（left 一直增加，right一直减少），要时刻保证， left < right 这个条件始终成立，注意Division函数中 这个条件就出现了3次
3. 特别留意每个循环后，互相赋值的顺序，你会发现，每个位置被赋值之前，它的值已经妥善保存在另外的地方了，这是个精巧的设计。

缺点

我曾经在用C#写过快排的算法，排序的数组规模是5000个数字左右，总会出现堆栈内存溢出，就是递归深度超出了堆栈的存储。以上面的例子来看，10个数字而已，就被分了六次，即QuickSort运行了六次。具体数学关系，有空会去研究。