Every day a Leetcode
题目来源:2008. 出租车的最大盈利
解法1:排序 + 二分查找 + 动态规划
将数组 rides 按照 endi 从小到大进行排序,记 m 为 rides 的大小,dp1 表示只接区间 [0,i] 内的乘客的最大盈利,显然 dp0 = 0,而对于 i∈[0,m],有两种情况:
- 对第 i 位乘客接单:由于前面已经对数组 rides 排序,因此我们可以通过二分查找来找到满足 endj ≤ starti 最大的 j,那么,设 earningi-1 = rides[i - 1][1] - rides[i - 1][0] + rides[i - 1][2],有 dp[i] = max(dp[i - 1], dp[j] + earning)。
- 不对第 i 位乘客接单:dp[i] = dp[i-1]。
于是,我们得到了状态转移方程:dp[i] = max(dp[i - 1], dp[j] + earning)。
代码:
/*
* @lc app=leetcode.cn id=2008 lang=cpp
*
* [2008] 出租车的最大盈利
*/
// @lc code=start
class Solution
{
private:
// 对数组 rides 按 end 从小到大排序
static bool cmp(const vector<int> &ride1, const vector<int> &ride2)
{
return ride1[1] < ride2[1];
}
public:
long long maxTaxiEarnings(int n, vector<vector<int>> &rides)
{
// 特判
if (n == 0 || rides.empty())
return 0;
sort(rides.begin(), rides.end(), cmp);
int m = rides.size();
// dp[i]: 接区间 [0, i] 内的乘客的最大盈利
vector<long long> dp(m + 1, 0);
// 初始化
dp[0] = 0;
// 状态转移
for (int i = 1; i <= m; i++)
{
int j = upper_bound(rides.begin(), rides.begin() + i - 1, rides[i - 1][0], [](int x, const vector<int> &r) -> bool
{ return x < r[1]; }) -
rides.begin();
int earning = rides[i - 1][1] - rides[i - 1][0] + rides[i - 1][2];
dp[i] = max(dp[i - 1], dp[j] + earning);
}
return dp[m];
}
};
// @lc code=end
结果:
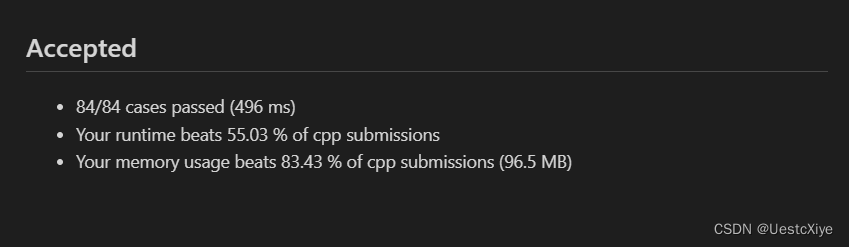
复杂度分析:
时间复杂度:O(mlogm),其中 m 是数组 rides 的长度。一次二分查找需要 O(logm) 的时间,共进行 m 次二分查找,总计的时间复杂度为 O(mlogm)。
空间复杂度:O(m),其中 m 是数组 rides 的长度。
解法2:动态规划 + 哈希表
使用哈希表 rideMap[end] 记录终点为 end 的所有乘客信息。不同于解法 1,我们使用 dp[i] 表示到达第 i 个地点时,能获取的最大盈利,显然有 dp[0] = 0,而对于 i∈[1,n],有两种情况:
- 选择一个终点为第 i 个地点的乘客 j:设这次盈利 earning = endj - startj + tipj,那么最大盈利为 dp[i] = dp[startj] + earning。
- 没有乘客在第 i 个地点下车:dp[i] = dp[i-1]。
于是,我们得到了状态转移方程:dp[i] = max(dp[i - 1], max(dp[startj] + endj - startj + tipj)。
注意,因为 unordered_map 内部是由哈希表实现的,哈希表中的每一项为一个桶,分别装着键和值,原 STL 中不包含 pair<int,int> 类型的键,不能够直接使用嵌套到哈希表中,所以需要自定义哈希值与判断相等函数。
代码:
// 哈希表 + 动态规划
class Solution
{
public:
long long maxTaxiEarnings(int n, vector<vector<int>> &rides)
{
// 特判
if (n == 0 || rides.empty())
return 0;
unordered_map<int, vector<vector<int>>> rideMap; //<end, {start, tip}>
for (const vector<int> &ride : rides)
{
int start = ride[0], end = ride[1], tip = ride[2];
rideMap[end].push_back({start, tip});
}
// dp[i]: 到达第 i 个地点时能获取的最大盈利
vector<long long> dp(n + 1, 0);
// 初始化
dp[0] = 0;
// 状态转移
for (int i = 1; i <= n; i++)
{
dp[i] = max(dp[i], dp[i - 1]);
for (vector<int> &ride : rideMap[i])
{
int start = ride[0], end = i, tip = ride[1];
int earning = end - start + ride[1];
dp[i] = max(dp[i], dp[start] + earning);
}
}
return dp[n];
}
};
结果:
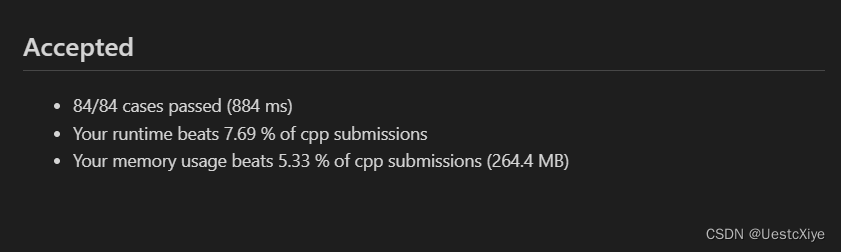
复杂度分析:
时间复杂度:O(m+n),其中 m 是数组 rides 的长度,n 是地点的数量。动态规划转移需要 O(n) 的时间,查询乘客信息需要 O(m) 的时间。
空间复杂度:O(m+n),其中 m 是数组 rides 的长度,n 是地点的数量。动态规划需要保存 n 个状态,哈希表需要保存 m 个乘客信息。





 文章介绍了两种方法解决LeetCode题目2008出租车的最大盈利问题,一种是通过排序、二分查找和动态规划,另一种是结合哈希表优化状态转移过程。两种方法都分析了时间复杂度和空间复杂度。
文章介绍了两种方法解决LeetCode题目2008出租车的最大盈利问题,一种是通过排序、二分查找和动态规划,另一种是结合哈希表优化状态转移过程。两种方法都分析了时间复杂度和空间复杂度。

















 1055
1055

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










