《机器学习》实验五:实现K-means聚类
《机器学习》实验五:实现K-means聚类
实验目的
- 了解聚类的基本概念
- 掌握K-means聚类算法的基本原理;
实验原理
- 聚类
将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合,这些对象与同一个簇中的对象彼此相似,与其他簇中的对象相异。“物以类聚,人以群分”,在自然科学和社会科学中,存在着大量的分类问题。聚类分析又称群分析,它是研究(样品或指标)分类问题的一种统计分析方法。聚类分析起源于分类学,但是聚类不等于分类。聚类与分类的不同在于,聚类所要求划分的类是未知的。聚类分析内容非常丰富,有系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类预报法等。
在机器学习中,聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常被称为无监督学习。 - K-means聚类算法
K-means聚类算法是一种迭代求解的聚类分析算法。算法思想是:需要随机选择k个对象作为初始的聚类中心,然后计算每个对象和各个聚类中心之间的距离,然后将每个对象分配给距离它最近的聚类中心。
K-means聚类算法的一般步骤如下所示:

图1 K-means聚类算法的一般步骤
实验内容与要求
- 数据预处理;
- 实现K-means聚类算法;
- 计算各簇的质心,打印结果;
- 绘制图像。
实验器材(设备、元器件)
处理器:Intel® Core™ i5-8300H CPU @ 2.30GHz
Python 3.9.0
matplotlib 3.4.0
numpy 1.23.4
实验步骤
- 数据预处理
给定的数据样本是data文件,将数据转存到K-means.txt中。读取这个文件,将顶点坐标转为浮点数,存储在一个列表中。代码如下:
# 读取数据
f = open('data/K-means.txt', 'r')
for line in f:
points.append(np.array(line.split(','), dtype=np.string_).astype(np.float64))
# print(points)
- 实现K-means聚类算法
首先,设置簇数k、最大迭代次数、均值向量变化量下界等参数。代码如下:
# 参数设置
# 簇数
k = 3
# 迭代次数
round = 0
# 最大迭代次数
ROUND_LIMIT = 50
# 均值向量变化量下界
THRESHOLD = 1e-10
接着初始化k个簇的质心,实现K-means算法,距离选择为欧式距离,当均值向量变化量足够小或达到最大迭代量时,退出K-means算法。代码如下:
# 随机取k个不重复的顶点作为初始质心
mean_vectors = random.sample(points, k)
# K-means算法
while True:
# 迭代次数自增
round += 1
# 初始化均值向量变化量
change = 0
# 清空对簇的划分
clusters = []
for i in range(k):
clusters.append([])
for point in points:
'''
argmin函数找出容器中最小的下标,在这里这个目标容器是
list(map(lambda vec: np.linalg.norm(melon - vec, ord = 2), mean_vectors)),
它表示melon与mean_vectors中所有向量的距离列表。
(numpy.linalg.norm计算向量的范数,ord = 2即欧几里得范数,或模长)
'''
c = np.argmin(
list(map(lambda vec: np.linalg.norm(point - vec, ord=2), mean_vectors))
)
clusters[c].append(point)
for i in range(k):
# 求每个簇的新均值向量
new_vector = np.zeros((1, 2))
for point in clusters[i]:
new_vector += point
new_vector /= len(clusters[i])
# 累加改变幅度并更新均值向量
change += np.linalg.norm(mean_vectors[i] - new_vector, ord=2)
mean_vectors[i] = new_vector
# 当均值向量变化量足够小或达到最大迭代量时,退出K-means算法
if round > ROUND_LIMIT or change < THRESHOLD:
break
- 计算各簇的质心,打印结果
簇的聚类结果保存在列表clusters中,其中每一个元素都是一个列表,列表的元素就是位于同一个簇中的顶点坐标。将同簇中各顶点坐标求和后取平均值即是该簇的质心坐标。打印迭代次数round和各个簇的质心坐标。代码如下:
# 打印结果
print('共迭代%d轮。' % round)
for i, cluster in zip(range(k), clusters):
# 求各簇的质心
centroid = []
x_mean = 0.0
y_mean = 0.0
for point in cluster:
x_mean += point[0]
y_mean += point[1]
x_mean /= len(cluster)
y_mean /= len(cluster)
centroid.append(x_mean)
centroid.append(y_mean)
print('簇%d的质心为:' % (i + 1), centroid)
- 绘制图像
绘制散点图,使得不同簇的顶点的颜色不同,同一个簇的顶点的颜色相同。代码如下:
# 绘图
colors = ['red', 'green', 'blue']
# 每个簇换一下颜色,同时迭代簇和颜色两个列表
for i, color in zip(range(k), colors):
for point in clusters[i]:
# 绘制散点图
plt.scatter(point[0], point[1], color=color)
plt.savefig('聚类结果.jpg')
plt.show()
- 实验结果
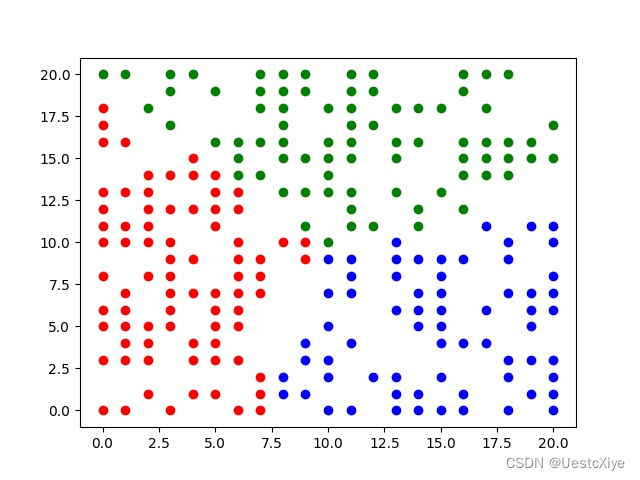
当k=3时,

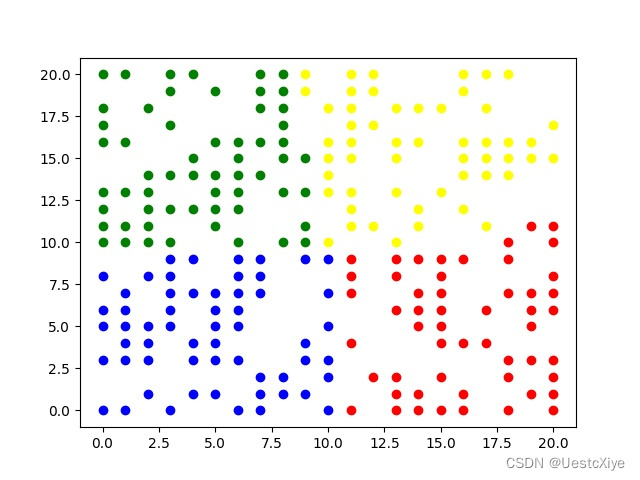
当k=4时,

当k=5时,

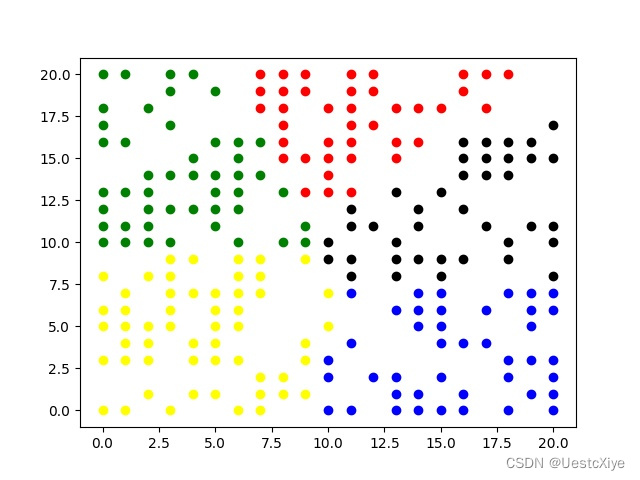
从上述实验结果可以看出,K-means算法能够将数据样本划分为指定个数的簇的集合。通过迭代计算,使得簇内距离尽可能小,簇间距离尽可能大。从绘制的散点图可以看出,该算法很好地达到了聚类的效果。
心得体会
本实验实现了K-means聚类,分别将簇的个数设置为3、4、5,得到了不同的聚类结果,实验效果良好。通过此次实验,很好地掌握了K-means聚类算法的基本原理,熟悉了Python第三方库——matplotlib和numpy的使用。
 K-means聚类算法实现与实验分析
K-means聚类算法实现与实验分析





 本文详细介绍了《机器学习》实验中K-means聚类算法的实现过程,包括实验目的、原理、步骤及结果。通过Python实现K-means算法,对不同簇数的聚类效果进行了展示,展示了数据预处理、质心计算、散点图绘制等关键步骤,并对实验结果进行了讨论。实验表明,K-means算法能有效地将数据样本划分为指定数量的簇,实现良好的聚类效果。
本文详细介绍了《机器学习》实验中K-means聚类算法的实现过程,包括实验目的、原理、步骤及结果。通过Python实现K-means算法,对不同簇数的聚类效果进行了展示,展示了数据预处理、质心计算、散点图绘制等关键步骤,并对实验结果进行了讨论。实验表明,K-means算法能有效地将数据样本划分为指定数量的簇,实现良好的聚类效果。

















 3657
3657

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










