图解利用栈实现递归函数的非递归计算

最新推荐文章于 2022-12-06 15:34:12 发布
原创 最新推荐文章于 2022-12-06 15:34:12 发布 · 748 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #栈 #递归 #算法

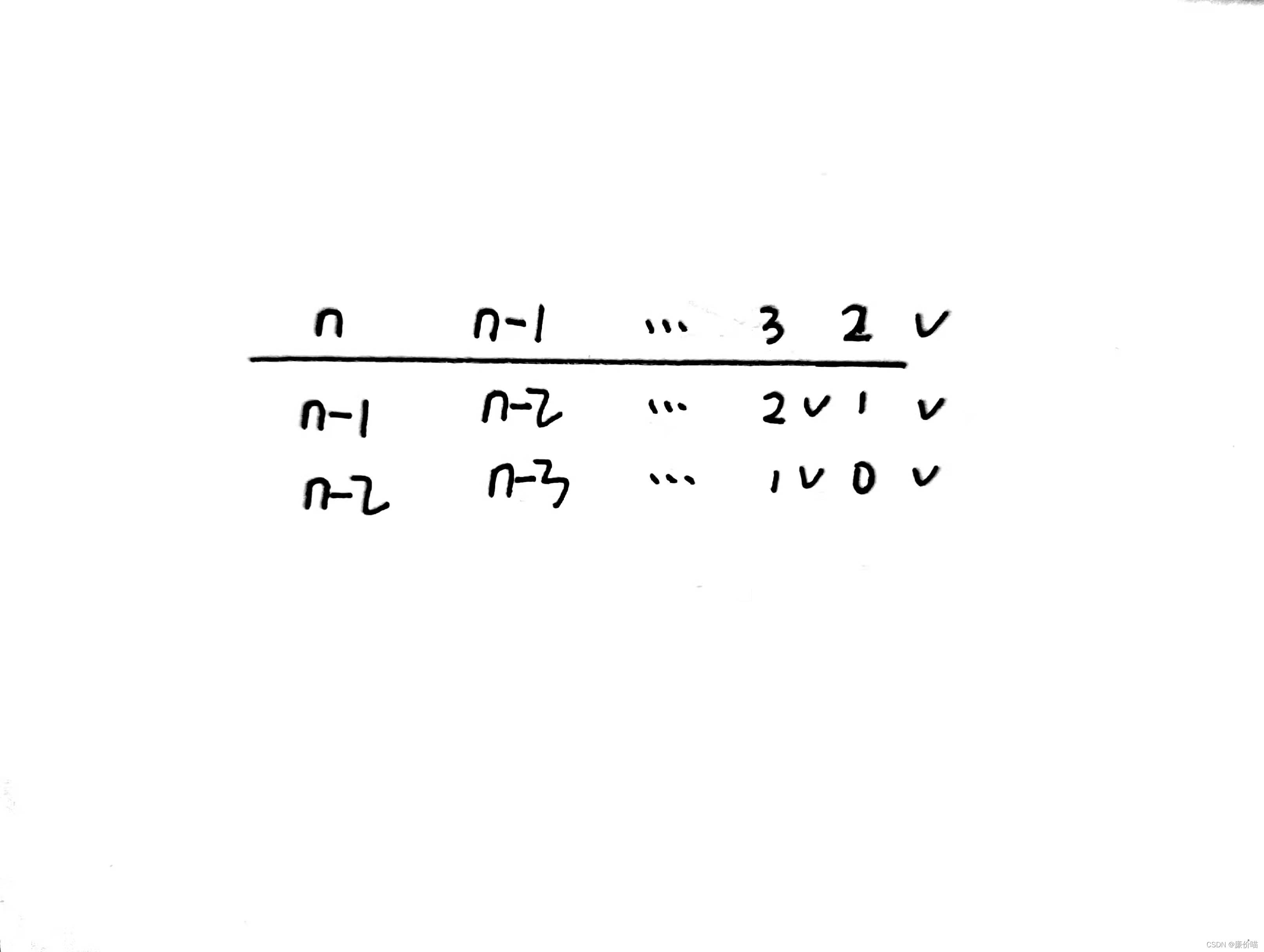
本文通过图解方式介绍如何利用栈来实现递归函数的非递归计算。作者在理解过程中发现，关键在于找出递归计算的规律，并利用栈的数据结构从后向前推导每个值。

例题

在这里插入图片描述

一开始我看网上说的是要模拟实际函数调用堆栈的行为
然后我就一直在想怎么模拟
比如我一开始想的是

n
n-1 n-2
n-1 n-3 n-4
n-1 n-3 n-5 n-6

这样
但是我不知道怎么存住数值
然后看了解析之后才发现这就是找规律而已……
堆栈也只是为了从后面把每一个 Pn(x) 求出来

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

最低0.47元/天 解锁文章
利用栈实现递归函数的非递归计算
北街lhy的博客
06-05 3323
题目：利用栈实现以下递归函数的非递归计算 分析： 这里我们需要使用栈的先进后出特性。我们可以看出，从n=2开始，每一个值便都与前两个值挂钩，且式子不变，我们可以从栈顶到栈底依次边出栈边计算，直至栈底，便可以得出最终结果。 代码如下： #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> struct Recursion { int no; int val; ...
快速排序（非递归）——C语言实现
qq_41890240的博客
04-12 5788
一、递归算法快速排序分析 在快速排序这篇文章中——>【快速排序点击这里】已经提到并分析了，递归会建立函数栈帧，递归的深度越深，占用栈区的空间就越大，栈区的大小一般是8M，10M。当深度足够深时，栈区的空间就会被用完，导致栈溢出，即便是加了小区间优化，依然会存在栈溢出的缺陷，所以我们必须寻求一种稳妥的方法，这种方法就是非递归实现。 二、非递归算法实现快速排序 2.1 需求分析 我们采用递归算法来实现快速排序时，我们递归的到底是什么？很简单，我们通过递归，就是再次调用该函数的功能，也就是单趟排序。那么我们
如何用栈实现递归与非递归的转换
05-07
递归与非递归转换的基础知识是能够正确理解三种树的遍历方法：前序、中序和后序。第一篇就是关于这三种遍历方法的递归和非递归算法。
数据结构:栈的应用-递归函数转非递归函数
04-19
演示了如何把低效率的递归函数转换成非递归的函数并完成相同的计算。
数据结构:使用栈实现递归函数的非递归计算
qq_44955742的博客
09-03 1174
对于以下一个递归函数，可用一个栈实现 ![递归函数](https://img-blog.csdnimg.cn/20200903205736982.png#pic_center) 用栈实现的C语言代码为： #include <stdio.h> #define Maxsize 10 //栈的最大容量，此时n能取的最大值为11 double p(int n, double x); int main(){ int n = 0; double x = 0; printf("输入n:",
【数据结构】利用栈实现递归函数的非递归计算
GW_Krystal的博客
09-01 1195
利用栈实现递归函数的非递归计算
java实现哈密顿路径，递归和非递归两种方式
04-13
本项目提供了两种Java实现方式来解决哈密顿路径：递归与非递归。 首先，让我们讨论递归方法。递归是通过函数自我调用来解决问题的一种策略。在哈密顿路径的递归实现中，通常会定义一个函数，该函数接受当前顶点和已...
排序算法6——图解归并排序及其递归与非递归实现
优快云_dzh的博客
12-14 1682
基本思想 归并排序就是利用归并的思想来实现排序。 原理是： 假设初始序列有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1， 然后两两归并，得到n/2（+1）个长度为2（或1）的有序的子序列 再两两归并…… 如此重复，知道得到一个长度为n的有序序列为止 这种排序方法称为 2路归并排序 归并排序递归方法实现 下面看递归的实现，思路是 先将数组通过mid拆成两半，首先对左边的子序...
全排列问题的细节讲解（递归：DFS、非递归实现）
一只攻城狮的博客
12-24 1474
全排列问题的细节讲解（递归：DFS、非递归实现） 在这里插入代码片 package Permutation; /** * @Description Full Permutation Algorithm * @author zhuwei * @Email zhu_wei2019@163.com * @version v1.0 */ public class FullPermutaion { public static void main(String[] args) { int[] n
算法图解之递归(一)(JAVA版本)
m0_53318344的博客
05-02 927
一步一步学习算法图解里面的算法
汉诺塔非递归算法 用栈 C语言
10-18
用栈来实现汉诺塔，要明白递归就是栈的重要应用之一，递归是系统自动调用栈来处理。
王道数据结构3.3.6——3、利用栈实现以下递归函数的非递归算法
Hillbox
10-14 1241
思路 代码 double p(int n,double x){ struct stack{ int no; double val; }st[MaxSize]; int top=-1,i; double fv1=1,fv2=2*x; for(i=n;i>=2;i--){ //入栈 top++; ...
利用栈实现递归函数的非递归计算（非递归求阶乘）
weixin_61866141的博客
10-16 1781
(5）返回处理：在栈不空的情况下，反复退出栈顶记录，根据记录中的返回地址进行题意规定的操作，即逐层计算当前的数值，直全栈空为止。(3）进人递归调用入口：当不满足递归结束条件时，逐层递归，将实参、返回地址及局部变量入栈，这一过程可用循环语句来实现。初始输入n=3，由于n大于1，不满足结束条件，将n=3进行存储表示F(3)未计算。计算n=n-1，n=2>1，不满足结束条件，将n=2进行存储表示F(2)未计算。计算n=n-1，n=1，满足结束条件，F(1)=1完成计算。（模拟递归分解的过程）（模拟递归求值过程）
[转]如何用栈实现递归与非递归的转换
weixin_30399055的博客
06-13 399
一.为什么要学习递归与非递归的转换的实现方法? 1)并不是每一门语言都支持递归的. 2)有助于理解递归的本质. 3)有助于理解栈,树等数据结构.二.递归与非递归转换的原理. 递归与非递归的转换基于以下的原理:所有的递归程序都可以用树结构表示出来.需要说明的是,这个"原理"并没有经过严格的数学证明,只是我的一个猜想,不过在至少在我遇到的例子中是适用的. 学习过树结构的人都知道,有...
[数据结构习题]用栈实现递归函数的非递归运算
weixin_64274123的博客
12-06 760
利用一个栈实现以下递归函数的非递归计算
利用栈将递归转化为非递归
m0_54223074的博客
03-03 791
1)设置一个工作栈存放递归工作记录（包括实参、 返回地址及局部变量等）。 (2)进入非递归调用入口（即被调用程序开始处） 将调用程序传来的实在参数和返回地址入 栈（递归程序不可以作为主程序，因而可认为初始是被某个调用程序调用。 (3)进入递归调用入口：当不满足递归结束条件时，逐层递归，将实参、 返回地址及局部变 量入栈，这一过程可用循环语句来实现一模拟递归分解的过程。 (4)递归结束条件满足，将到达递归出口的给定常数作为当前的函数值。 (5)返回处理：在栈不空的情况下，反复退出栈顶记录，根据记录中的返回地址
栈实现斐波那契数列递归过程的非递归模拟
幽兰止水
09-27 6892
//斐波那契数列求和的非递归算法 //非递归算法利用栈作工具，栈的数据类型      struct Node {         int n,tag; }; //利用栈作工具，非递归算法 long Fibnacci ( long N )   {
递归函数运行逻辑
最新发布
11-07
用户之前关注过递归函数的具体实现（引用[3]里提到变量地址的差异），说明ta可能更关心运行时细节而非理论。因此需要着重解释递归栈的物理层面，比如： - 每次递归调用如何创建独立的栈帧 - 变量隔离性（同名变量...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值