Adam 算法（Adaptive Moment Estimation）

原创于 2025-11-06 08:00:00 发布 · 2.2k 阅读

41 ·

CC 4.0 BY-SA版权

文章标签：

#算法

深度学习_02 同时被 2 个专栏收录

20 篇文章

订阅专栏

算法设计与分析（含刷题）

10 篇文章

订阅专栏

该文章已生成可运行项目，

Adam 算法（Adaptive Moment Estimation）是深度学习领域极具影响力的优化算法，它融合了动量法（Momentum）和RMSProp的优势，通过自适应调整每个参数的学习率，实现高效且稳定的模型训练。

一、算法背景与核心设计

Adam 由 Diederik P. Kingma 和 Jimmy Ba 于 2014 年提出，旨在解决传统随机梯度下降（SGD）的两大痛点：

SGD 收敛慢且对学习率敏感；
传统自适应学习率算法（如 AdaGrad、RMSProp）缺乏 “动量” 概念，难以应对复杂损失曲面。

Adam 的核心是同时跟踪梯度的一阶矩（均值，体现梯度方向的稳定性）和二阶矩（方差，体现梯度的波动程度），并为每个参数自适应调整学习率。

二、数学推导：从初始化到参数更新

Adam 的完整流程可分为5 个关键步骤，每一步都有明确的物理意义：

1. 初始化

模型参数：θ0（如权重w、偏置b）；
一阶矩（动量）：m0=0（记录梯度的指数移动平均）；
二阶矩（梯度平方的移动平均）：v0=0（记录梯度波动的程度）；
超参数：学习率α（默认 0.001）、一阶矩衰减率β1（默认 0.9）、二阶矩衰减率β2（默认 0.999）、数值稳定项ϵ（默认 $10^{-8}$ ）。

2. 计算当前梯度

对于时间步t，计算小批量数据的梯度：

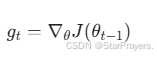
其中J(θ)是损失函数，∇θ表示对参数θ求偏导。

3. 更新一阶矩（动量项）

一阶矩mt是梯度的指数加权移动平均，体现梯度方向的 “惯性”：

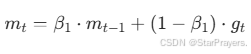
β1越接近 1，越重视历史梯度（如β1=0.9表示当前梯度仅占 10% 权重，历史梯度占 90%）；
该机制可平滑梯度噪声，让参数更新方向更稳定。

4. 更新二阶矩（梯度平方的移动平均）

二阶矩vt是梯度平方的指数加权移动平均，体现梯度的波动幅度：

β2越接近 1，越重视历史梯度的波动（如β2=0.999表示当前梯度平方仅占 0.1% 权重）；
该机制为自适应学习率提供依据：梯度波动大的参数，学习率会自动减小；波动小的参数，学习率会自动增大。

5. 偏差校正

由于m0和v0初始为 0，训练初期的mt和vt会偏向 0。因此需通过偏差校正消除这种偏差：

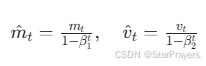
当t增大时，β1t和β2t趋近于 0，校正项趋近于 1，偏差的影响逐渐消失。

6. 参数更新

最终，每个参数的更新公式为：

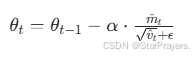
是自适应学习率的核心：结合了梯度方向的稳定性（）和梯度波动的程度（），让每个参数的更新步长 “因地制宜”。

三、直观理解：梯度下降的 “智能导航员”

可以将 Adam 比作 “下山导航员”：

一阶矩m^t：记录 “历史行走方向”，避免因局部噪声偏离大方向（类似动量法的 “惯性”）；
二阶矩v^t：评估 “山势陡峭程度”（梯度波动大则山势陡），陡峭处小步走（减小学习率），平缓处大步走（增大学习率）；
偏差校正：训练初期 “校准指南针”，确保起步阶段的方向不偏航。

四、优缺点与适用场景

1.优点

收敛速度快：在深层网络（如 Transformer、ResNet）中，收敛速度通常比 SGD 快 2-5 倍；
自适应学习率：无需手动调整全局学习率，对不同参数 “因材施教”；
鲁棒性强：能适应损失函数的 “峡谷”（曲率变化大）或 “平原”（梯度小）地形，不易震荡或停滞；
对新手友好：默认参数（α=0.001,β1=0.9,β2=0.999,ϵ= $10^{-8}$ ）在大多数任务中表现良好。

2.缺点

泛化性可能不足：自适应学习率可能让模型陷入 “尖锐的局部极小值”，在小数据集上泛化能力可能不如 SGD；
内存占用稍高：需为每个参数存储一阶矩和二阶矩（额外两个张量），但现代硬件可轻松承载；
超参数仍需关注：虽然默认参数好用，但某些任务（如强化学习）可能需要调整β1、β2或学习率。

3.适用场景

大规模数据集（如 ImageNet、BERT 预训练）；
深层神经网络（CNN、RNN、Transformer）；
需快速迭代的实验（如模型原型设计）；
稀疏梯度任务（如自然语言处理中的文本分类）。

五、变种与扩展

为解决 Adam 的局限性，研究者提出了诸多变种：

AdamW：在 Adam 基础上加入权重衰减（Weight Decay），增强正则化能力，缓解过拟合；
AMSGrad：修改二阶矩的更新方式，确保其单调递增，提升收敛稳定性；
AdaBound：为学习率添加上下界约束，结合 Adam 的自适应能力和 SGD 的泛化能力。

六、代码实践：手动实现与框架调用

1. 手动实现（Python）

import numpy as np

class AdamOptimizer:
    def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
        self.learning_rate = learning_rate
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.m = None  # 一阶矩
        self.v = None  # 二阶矩
        self.t = 0     # 时间步

    def update(self, params, grads):
        if self.m is None:
            self.m = np.zeros_like(params)
            self.v = np.zeros_like(params)
        self.t += 1
        
        # 更新一阶、二阶矩
        self.m = self.beta1 * self.m + (1 - self.beta1) * grads
        self.v = self.beta2 * self.v + (1 - self.beta2) * (grads ** 2)
        
        # 偏差校正
        m_hat = self.m / (1 - self.beta1 ** self.t)
        v_hat = self.v / (1 - self.beta2 ** self.t)
        
        # 参数更新
        params -= self.learning_rate * m_hat / (np.sqrt(v_hat) + self.epsilon)
        return params

2. 框架调用（TensorFlow/Keras）

以 MNIST 手写数字识别为例：

import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 加载数据
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(-1, 784) / 255.0  #  flatten + 归一化

# 构建模型
model = Sequential([
    Dense(25, activation='sigmoid'),
    Dense(15, activation='sigmoid'),
    Dense(10, activation='linear')  # 配合SparseCategoricalCrossentropy(from_logits=True)
])

# 编译模型：使用Adam优化器
model.compile(
    optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3),
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    metrics=['accuracy']
)

# 训练模型
model.fit(X_train, y_train, epochs=10, batch_size=32, validation_split=0.2)

本文章已经生成可运行项目