一、多分类(Multiclass Classification)
1.1 多分类任务的定义
多分类任务是指将样本划分到三个或更多类别中的任务(区别于二分类的 “是 / 否”)。
- 二分类示例:将样本分为 “class 1” 和 “not 1” 两类,用逻辑回归即可解决。
- 多分类示例:将样本分为 4 个类别(红叉、蓝圈、黄方块、紫三角),需要更复杂的模型(如 Softmax 回归、带 Softmax 输出的神经网络)。
1.2 多分类的核心模型:Softmax 回归
Softmax 回归是逻辑回归在多分类场景的推广,核心是通过 “Softmax 函数” 将线性输出转化为类别概率分布。
①逻辑回归 vs. Softmax 回归(Cost 部分)
-
逻辑回归(二分类):
-
输入
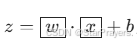 ,通过 Sigmoid 函数输出类别 1 的概率:
,通过 Sigmoid 函数输出类别 1 的概率: -
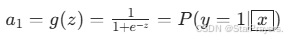
-
类别 0 的概率为
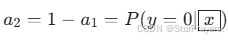 。
。 -
损失函数(交叉熵损失)为:
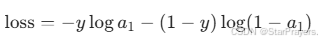
-
其中 y∈{0,1} 是真实标签。
-
-
Softmax 回归(多分类):
-
.假设共有 N 个类别,先计算每个类别的线性得分 z1,z2,…,zN(即
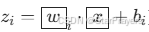 ),再通过 Softmax 函数将得分转化为概率:
),再通过 Softmax 函数将得分转化为概率: -
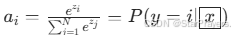
-
所有 ai 之和为 1,满足概率的基本性质。
-
损失函数(交叉熵损失)为:
-
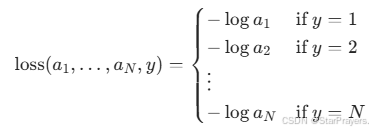
-
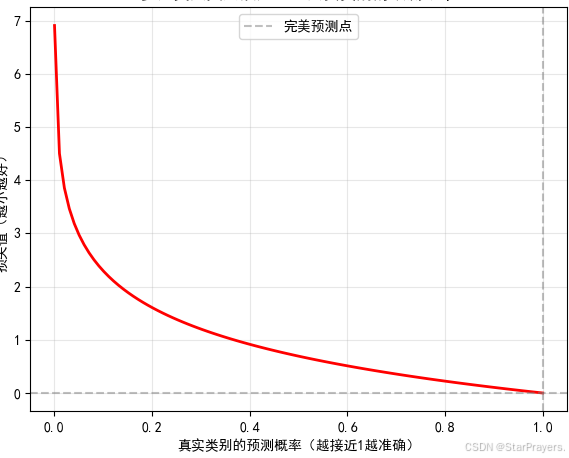
直观理解:若真实类别是 j,则损失是 “对预测概率 aj 取负对数”
-
aj 越接近 1,损失越小;越接近 0,损失越大。
-
1.3 带 Softmax 输出的神经网络
在深度学习中,我们可以将 Softmax 作为神经网络的输出层,处理多分类任务。
以识别手写数字的 MNIST 数据集(10 个类别:0-9)为例,网络结构通常为:
- 隐藏层:使用 ReLU 激活(引入非线性,高效训练),如 “25 个神经元的 Dense 层 + 15 个神经元的 Dense 层”。
- 输出层:10 个神经元,使用 Softmax 激活,输出 10 个类别各自的概率(如
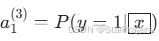 ,
,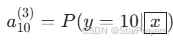 。
。
这种结构的本质是:隐藏层提取输入的非线性特征,输出层通过 Softmax 将特征映射为类别概率。
1.4 实战:TensorFlow/Keras 实现多分类模型(MNIST with softmax)
基于 TensorFlow/Keras 的代码框架,步骤如下:
- ①定义模型(specify the model):
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
model = Sequential([
Dense(units=25, activation='relu'), # 隐藏层1:25个神经元,ReLU激活
Dense(units=15, activation='relu'), # 隐藏层2:15个神经元,ReLU激活
Dense(units=10, activation='softmax') # 输出层:10个类别,Softmax激活
])
- ②定义损失函数(specify loss and cost):
多分类任务通常使用稀疏分类交叉熵损失(SparseCategoricalCrossentropy):
from tensorflow.keras.losses import SparseCategoricalCrossentropy
model.compile(loss=SparseCategoricalCrossentropy())
- ③训练模型(Train on data):
model.fit(X, y, epochs=100) # X是输入特征,y是真实标签(如0-9的整数)
1.5 数值稳定性优化(Numerical Roundoff Errors)
在深度学习中,直接计算 Softmax 或 Sigmoid 可能因数值溢出(如 ![]() 当
当 ![]() 很大时趋于无穷)导致计算不稳定。因此需要更精确的实现方式:
很大时趋于无穷)导致计算不稳定。因此需要更精确的实现方式:
①. 逻辑回归的数值稳定优化
对于二分类任务,避免直接计算 Sigmoid 后再求损失,而是直接对线性输出(logits)计算损失:
# 不推荐:先过Sigmoid再算损失
model = Sequential([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
Dense(units=1, activation='sigmoid')
])
model.compile(loss=BinaryCrossentropy())
# 推荐:对logits直接计算损失(数值更稳定)
model = Sequential([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
Dense(units=1, activation='linear') # 输出层无激活,直接输出logits
])
model.compile(loss=BinaryCrossentropy(from_logits=True))
# 预测时再用Sigmoid转换为概率
logits = model.predict(X)
prob = tf.nn.sigmoid(logits)
②. Softmax 回归的数值稳定优化
同理,多分类任务也应对输出层的 logits 直接计算损失:
# 不推荐:先过Softmax再算损失
model = Sequential([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
Dense(units=10, activation='softmax')
])
model.compile(loss=SparseCategoricalCrossentropy())
# 推荐:对logits直接计算损失(数值更稳定)
model = Sequential([
Dense(units=25, activation='relu'),
Dense(units=15, activation='relu'),
Dense(units=10, activation='linear') # 输出层无激活,直接输出logits
])
model.compile(loss=SparseCategoricalCrossentropy(from_logits=True))
# 预测时再用Softmax转换为概率
logits = model.predict(X)
prob = tf.nn.softmax(logits)
这种优化的核心是将 “激活函数 + 损失计算” 合并为更高效的数值计算方式,避免中间步骤的精度损失或溢出。
1.6 扩展:多分类的其他场景与技巧
- 类别不平衡问题:若某类别样本极少,可通过加权损失(如
class_weight参数)或数据增强来缓解。 - 多标签分类:区别于 “每个样本仅属于一个类别” 的多分类,多标签分类允许样本同时属于多个类别(如一张图片同时包含 “猫” 和 “狗”),此时输出层通常用 Sigmoid 激活(每个类别独立预测),损失用二元交叉熵损失。
- 模型评估指标:多分类任务常用准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1 分数等指标,需根据业务场景选择(如医疗诊断更关注召回率,避免漏诊)。
二、多标签分类(Multi-label Classification)
2.1 多标签分类的任务定义
多标签分类是指一个样本可以同时属于多个类别的分类任务(区别于 “多分类任务中每个样本仅属于一个类别”)。
- 想象第一张图:同时包含 “car(汽车)” 和 “pedestrian(行人)”,所以标签为 y=
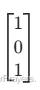 (“1” 表示存在该类别,“0” 表示不存在)。
(“1” 表示存在该类别,“0” 表示不存在)。 - 想象第二张图:仅包含 “pedestrian(行人)”,标签为 y=
 。
。 - 想象第三张图:同时包含 “car(汽车)” 和 “bus(公交车)”,标签为 y=
 。
。
2.2 多标签分类与多分类的核心区别
| 维度 | 多分类(Multiclass) | 多标签分类(Multi-label) |
|---|---|---|
| 类别关系 | 互斥(一个样本仅属于一个类别) | 非互斥(一个样本可属于多个类别) |
| 标签形式 | 单个整数(如 y∈{0,1,2,3}) | 二进制向量(如 y∈{0,1}3,每个维度对应一个类别是否存在) |
| 输出层激活 | Softmax(输出概率和为 1) | 多个 Sigmoid(每个类别独立输出概率,和不一定为 1) |
| 损失函数 | 分类交叉熵(如 SparseCategoricalCrossentropy) | 多个二元交叉熵(如 BinaryCrossentropy,每个类别独立计算) |
2.3 多标签分类的模型结构
两种模型构建思路:
①独立模型法(训练多个二分类模型)
对每个类别(如 car、bus、pedestrian)单独训练一个二分类神经网络:
- 模型 1:输入图片 → 输出 “是否有 car”(Sigmoid 激活,输出 0-1 概率)。
- 模型 2:输入图片 → 输出 “是否有 bus”(Sigmoid 激活)。
- 模型 3:输入图片 → 输出 “是否有 pedestrian”(Sigmoid 激活)。
这种方法的优点是每个类别独立训练,逻辑简单;缺点是重复计算(多个模型共享底层特征却重复训练),效率低。
②多输出单模型法(共享特征的多输出网络)
训练一个共享隐藏层的多输出神经网络:
- 隐藏层:提取图片的通用特征(如边缘、形状等),所有类别共享这些特征。
- 输出层:有 3 个神经元,每个神经元对应一个类别,使用Sigmoid 激活(因为每个类别是独立的二分类问题,输出 0-1 的概率)。
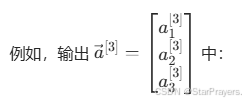
- a1[3] 是 “存在 car” 的概率,
- a2[3] 是 “存在 bus” 的概率,
- a3[3] 是 “存在 pedestrian” 的概率。
这种方法的优点是共享特征提取,训练高效,参数更少;是工业界更常用的方案。
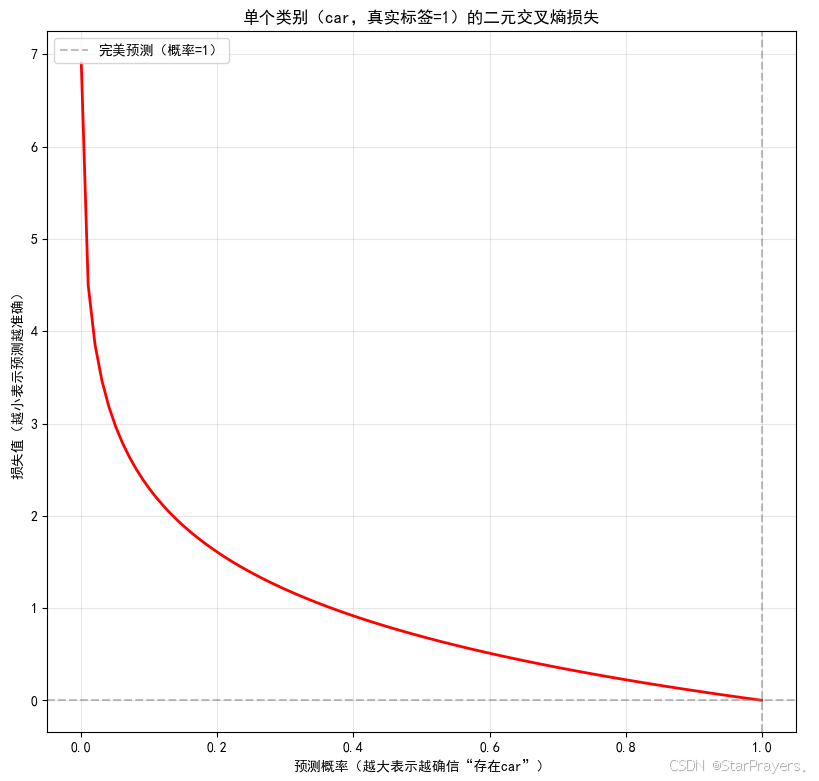
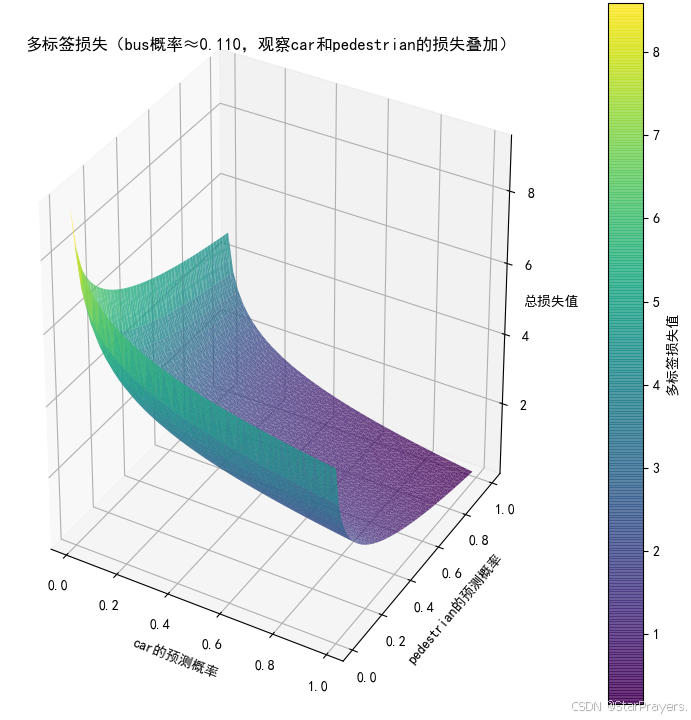
2.4 多标签分类的损失函数
由于每个类别是独立的二分类问题,多标签分类的损失函数是多个二元交叉熵损失的和。
对于单个样本,若真实标签为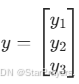 (yi∈{0,1}),模型输出为
(yi∈{0,1}),模型输出为 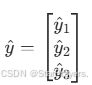 (y^i 是 Sigmoid 输出的概率),则损失为:
(y^i 是 Sigmoid 输出的概率),则损失为:
![]()
在框架中(如 TensorFlow/Keras),可直接使用 BinaryCrossentropy 损失函数,因为它会对每个输出维度独立计算二元交叉熵并求和。
2.5 多标签分类的应用场景
多标签分类在现实中非常常见,典型场景包括:
- 图像标注:一张图片可能同时包含 “猫”“狗”“草地” 等多个标签。
- 文本分类:一篇新闻可能同时属于 “科技”“经济”“国际” 等多个类别。
- 医疗诊断:一个病人可能同时患有 “高血压”“糖尿病” 等多种疾病。
2.6 扩展:多标签分类的评估指标
由于标签非互斥,多分类的 “准确率” 指标不再适用,需采用更适合的指标:
- 精确率(Precision):模型预测为 “存在” 的类别中,真正存在的比例(
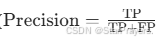 )。
)。 - 召回率(Recall):真实存在的类别中,模型预测为 “存在” 的比例(
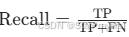 )。
)。 - F1 分数:精确率和召回率的调和平均(
 ),综合两者性能。
),综合两者性能。 - Hamming 损失:预测错误的标签数占总标签数的比例,衡量整体标签预测的准确性。






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








