工坊实验室 | CALCULATE 的嵌套使用

最新推荐文章于 2025-05-14 22:13:22 发布
原创 最新推荐文章于 2025-05-14 22:13:22 发布 · 934 阅读 · 4 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#可视化 #数据分析

本文通过实例探讨了在DAX中嵌套使用CALCULATE函数的情况，解释了内外层条件的关系及KEEPFILTERS函数的作用。总结了CALCULATE函数的筛选顺序和条件冲突处理，强调了内外层筛选条件的交互影响。

前言：
研究DAX函数不能抱着轻视它的心态，DAX简约而不简单，它的设计使得用户上手速度很快，但是要深入掌握一种函数的原理还是需要一定的耐心，投入相当的精力。

课 题 背 景

有时在表达式中我们会嵌套使用多个Calculate函数，多层条件之间的相互作用让很多小伙伴感到困惑，多层条件的叠加结果是取交集呢还是取并集呢，今天我们就来研究一下

01数据准备

file

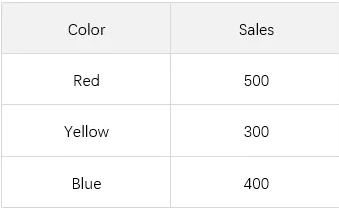
为了方便理解和解读实验结果，我们准备了非常简单的数据。一种商品系列的销售额，该商品系列有三种颜色——Red、Yellow、Blue，三种颜色分别对应一个销售额。

02尝试建模

我们构造如下几个度量值：

红色系列的销售额：

 Sales of Red =
CALCULATE ( SUM( Sales[Sales] ), 'Sales'[Color]= "Red" )

红黄系列的销售合计：

Sales of Red andYellow =
CALCULATE (
    SUM ( Sales[Sales] ),
    'Sales'[Color] = "Red"
        ||'Sales'[Color] = "Yellow"
)

红蓝系列的销售合计：

 Sales of Red and Blue = 
CALCULATE (
最低0.47元/天 解锁文章
PowerPivot基础知识
weixin_58074492的博客
03-02 675
FILTER将一个表表达式作为第一个参数，并遍历该表的所有行，检查第二个参数中提供的条件。ALLSELECTED相对清除筛选功能，根据筛选器(透视表筛选，切片器等，表中所有数据)而变。关系函数，将事实表的指定列关联到维度表，返回的是一个表，通常和SUMX搭配使用。筛选器函数，清除指定表/列的筛选功能，保留其他表/列的筛选功能。筛选器函数，除了指定列之外，清除其他列的筛选条件。('销售表'[金额]),'地区表'[区域]=筛选器函数，清除指定表（或列）的筛选功能。('产品表','产品表'[产品大类]=
从入门到入土：[SEED-Lab]- Packet Sniffing and Spoofing Lab|嗅探与欺骗实验|详细说明|实验步骤|实验截图
Q_U_A_R_T_E_R的博客
11-04 9638
此博客仅用于记录个人学习进度，学识浅薄，若有错误观点欢迎评论区指出。欢迎各位前来交流。（部分材料来源网络，若有侵权，立即删除） 本人博客所有文章纯属学习之用，不涉及商业利益。不合适引用，自当删除！ 若被用于非法行为，与我本人无关 [SEED-Lab]-Packet Sniffing and Spoofing Lab实验环境PDF文件实验步骤环境配置Labsetup操作步骤Lab Task Set 1: Using Scapy to Sniff and Spoof PacketsTask 1.1: Snif
PowerPivot——DAX（函数）
前景
07-06 1186
PowerPivot——DAX（函数）
学习CALCULATE函数（二）修订版
Fabric丨白茶
06-08 1234
之前呢，白茶分享了一些CALCULATE的心得，但是要知道我们在对数据进行分析的时候，往往是多条件参考的，比如说哪个区域、哪个时间点、哪个状态的销售的最好，这就很明显需要我们在计算的时候把这些选项算进去。 在纸上计算很容易，但是DAX中如何进行呢？ 来，看下面的例子： 这是我们在上一期使用的示例文件，现在我添加了一个下面的维度表： 这样的话昨天我们的计算公式就有了很大的调整空间。 销售 = VAR SQ = CALCULATE ( [数量], FILTER ( '表', [条件] = "N".
DAX Calculate的使用说明
Fluffy的百宝箱
04-12 1万+
对数据进行建模分析时经常会使用到DAX中的Calculate函数，这个函数微软给的中文解释是“在筛选器修改的上下文中对表表达式进行求值。”读起来很是绕口，但实际上Calculate函数可以看做是类似Excel内置函数Sumif的增强版，实现的功能是在特定筛选条件的基础上对数据进行计算，多于SUM, MIN, MAX, COUNTROWS等有聚合意义的函数一起使用。 Calcuate函数使用格式为...
power pivot关于Calculate删选函数的使用
weixin_44593546的博客
01-21 2385
Calculate函数 使用说明：Calculate（’[列]，【表】【列】外加条件1，【表】【列】外加条件1…【表】【列】外加条件N） 比如要删选出是其他的对应的金额是总计是多少的话就是表达式为： CALCULATE(sum([金额]，[四大类]=“其他”） 或者是 CALCULATE(销售金额合计单店 ##就是点击一下CALC上面一个单元格，[四大类]=“其他”） ** 注意：CALCUL...
calculate.rar_calculate指令_calculate数学
09-21
在实际应用中，calculate可以与各种编程语言结合使用，通过调用calculate的API或者子进程来实现动态的数学计算。例如，在Python中，可以使用os模块的system方法调用calculate指令，处理那些超出Python内置数学库能力...
calculate.zip_c# calculate_c#calculate算法
09-24
6. **递归（Recursion）**：在`EvaluateExpression()`方法中，可能会使用到递归来处理嵌套的括号表达式。递归是指函数调用自身，通常用于解决分治问题或表示具有层次结构的问题。 7. **异常处理（Exception ...
calculate.zip_calculate计算器_feet9mj
09-14
在"calculate"项目中，这个过程可能是由一个自定义的解析器类完成的，它可以识别和处理各种运算符，包括括号内的嵌套运算。 在"calculate.zip"的压缩包中，包含的"calculate"文件很可能就是整个项目的源代码。通过...
从叠加两层CALCULATE，发现的一些DAX基础知识中的细节
weixin_38775843的博客
02-09 405
CALCULATE 函数会将外部的行上下文转换为 CALCULATE 内的是选器上下文，只要认真学习了 DAX 必然都会知道这一点。只是，有一个细节我当时没有掌握到，就是：它转换的筛选上下文是给到该CALCULATE 的第一参数的，第二参数及其他参数不会受到这个筛师上下文的影响。
power bi中的calculate函数解析
程志伟的博客
11-14 1268
power bi中的calculate函数解析
Power Pivot常用函数
qq_52421831的博客
09-15 7117
Power Pivot常用函数
Power Pivot——常用DAX 函数
m0_47147246的博客
06-27 2224
Power Pivot——常用DAX 函数
DAX权威指南2：CALCULATE 与 CALCULATETABLE
qq_56591814的博客
05-14 1534
在DAX中，CALCULATE和CALCULATETABLE是唯一能够修改筛选上下文的函数。CALCULATE用于返回标量值，而CALCULATETABLE返回表。通过CALCULATE，可以创建新的筛选上下文、覆盖或移除现有筛选条件，从而简化计算过程。例如，在计算Contoso品牌的毛利率时，传统方法需要使用FILTER函数进行迭代计算，而通过CALCULATE可以直接复用已有度量值，仅需添加筛选条件即可。CALCULATE的工作原理包括：筛选参数是表（即使使用布尔条件也会转换为表形式），同一列的筛选器会
Dax 函数~ Calculate 与Calculatetable
qq_43632431的博客
11-08 647
其中销量表和销售人员表是通过销售进行关联的。可以看出不同的使用方案结果展示有差异。(1) 都是DAX中的重要函数，用于创建计算上下文。(3) 都支持使用筛选器作为参数。(2) 都可以修改筛选上下文。'销售表'[商品名称]
DAX函数大全
weixin_33968104的博客
11-12 1万+
针对PowerPivot的DAX函数参考 一、筛选函数 1、ALL函数：返回表中的所有行货返回列中的所有值，同时忽略可能已应用的任何筛选器，此函数可用于清除筛选器对表中的所有行创建计算，返回删除了筛选器的表或列的值 语法:ALL({<table>|<column>[,<column>[,<column&g...
<Excel> 数据分析之Power Pivot常用函数（持续更新）
热门推荐
su_2018的博客
10-29 2万+
目录 RELATED函数 RELATEDTABLE RANK.EQ COUNTROWS CALCULATE DIVIDE RELATED函数 RELATED(ColumnName) RELATED(返回的对应值的列名） →从其他表返回相关值 类似于Excel中的Vlookup,Power Query中的合并查询RELATED 函数要求当前表与包含相关信息的表之...
PowerPivot的DAX函数实战
zhudaxia_的博客
10-23 3871
针对PowerPivot的DAX函数参考 一、筛选函数 1、ALL函数：返回表中的所有行货返回列中的所有值，同时忽略可能已应用的任何筛选器，此函数可用于清除筛选器对表中的所有行创建计算，返回删除了筛选器的表或列的值 &lt;span style="color:#000000"&gt;语法:ALL({&lt;table&gt; | &lt;column&gt;[, &lt;column&gt...
闲扯：Excel 2013的PowerPivot及其它
数据库天地
11-01 321
Excel 2013的RTM 出来几天了，用了一下。 以下是一些感受， 纯属胡扯： 1，安装问题 Excel 2010的PowerPivot常出现安装问题，现在没有了，内置了，只需要加载。 而且，Excel 2013已经使用Xvelocity引擎，即使不使用PowerPivot，也可以导入海量数据。 2，关系问题 Excel 2013的表可以创建关系，也可以进行Dax Quer...
题目描述 光为了解决 C5I 三角地划分 ，写出了以下递归函数。 #include <stdio.h> long long f(int n) { if(n==3) return 1; long long fn=0; for(int i=3;i<=n;i++) { if(i==3||i==n) { fn+=f(n-1); } else { fn+=f(n-i+2)*f(i-1); } } return fn; } int main(){ int n; scanf("%d",&n); printf("%lld\n",f(n)); return 0; } 但是，提交后她发现超时了！通过观察递归的流程，她发现了程序可以进一步优化！ 具体而言，她引入这个优化：进入函数 f(x) 后，如果发现 f(x) 之前已经被计算过了，那么直接返回之前计算过的答案。否则，正常计算 f(x) ，并且在末尾记录下 f(x) 的值，也就是返回值，以便下次使用。 她设置了一个参数 op ，当且仅当 op=1 时，启用这个优化。 她希望了解输出函数的调用过程，也就是运行过程。然后，她还想知道优化的效果。具体方式如下： 初始时，缩进空格个数为 0 。具体格式如下： 进入函数 f(n) 时，先输出缩进，再输出 calculate begin f({n})；然后，缩进个数增加 1 。 如果 f(n) 没有被计算过或优化没有启用，则退出进行计算的函数 f(n) 时，缩进个数减少 1 ，然后先输出缩进，再输出 calculate end return f({n}) = {f(n)}。 如果 f(n) 已经被计算过且优化被启用，则不用再计算一遍 f(n) ，直接返回之前计算过的值。在这之前，然后，缩进个数减少 1 ，然后先输出缩进，再输出 calculated before return f({n}) = {fn}。 参见样例，你可能获得更好的题目理解。 最后输出两行，第一行为 answer f({n}) = {f(n)}，表示计算的答案。 第二行为 total function invoked count = {count}，其中 count 表示 f(x) 被调用的次数。 其中，“缩进”是将字符串 "| " （1 个竖线加 3 个空格）重复缩进个数次。 你可能需要用到的输出格式符： "calculate begin f(%d)\n" "calculate end return f(%d) = %lld\n" "calculated before return f(%d) = %lld\n" "answer f(%d) = %lld\n" "total function invoked count = %lld\n" 输入 一行两个整数 op,n 。 数据保证 op∈{0,1},3≤n≤13 。 输出 对于每组数据，输出很多行。 输入样例 1 0 4 输出样例 1 calculate begin f(4) | calculate begin f(3) | calculate end return f(3) = 1 | calculate begin f(3) | calculate end return f(3) = 1 calculate end return f(4) = 2 answer f(4) = 2 total function invoked count = 3 输入样例 2 1 4 输出样例 2 calculate begin f(4) | calculate begin f(3) | calculate end return f(3) = 1 | calculate begin f(3) | calculated before return f(3) = 1 calculate end return f(4) = 2 answer f(4) = 2 total function invoked count = 3 输入样例 3 1 5 输出样例 3 calculate begin f(5) | calculate begin f(4) | | calculate begin f(3) | | calculate end return f(3) = 1 | | calculate begin f(3) | | calculated before return f(3) = 1 | calculate end return f(4) = 2 | calculate begin f(3) | calculated before return f(3) = 1 | calculate begin f(3) | calculated before return f(3) = 1 | calculate begin f(4) | calculated before return f(4) = 2 calculate end return f(5) = 5 answer f(5) = 5 total function invoked count = 7 输入样例 4 0 5 输出样例 4 calculate begin f(5) | calculate begin f(4) | | calculate begin f(3) | | calculate end return f(3) = 1 | | calculate begin f(3) | | calculate end return f(3) = 1 | calculate end return f(4) = 2 | calculate begin f(3) | calculate end return f(3) = 1 | calculate begin f(3) | calculate end return f(3) = 1 | calculate begin f(4) | | calculate begin f(3) | | calculate end return f(3) = 1 | | calculate begin f(3) | | calculate end return f(3) = 1 | calculate end return f(4) = 2 calculate end return f(5) = 5 answer f(5) = 5 total function invoked count = 9 做题
最新发布
10-26
<think>题目要求我们实现一个递归函数，并且根据op参数决定是否启用记忆化优化（Memoization）。同时，我们需要按照特定的格式输出函数的调用过程和结果，并统计函数被调用的总次数。 观察题目给出的递归函数： 当n=3时，返回1。 否则，对于i从3到n（包括n）进行循环： 如果i等于3或者i等于n，那么 fn += f(n-1) 否则， fn += f(n-i+2) * f(i-1) 我们需要修改这个函数，加入以下功能： 1. 根据op是否启用记忆化优化（用一个全局数组来存储已经计算过的f(n)的值）。 2. 输出调用的过程，包括缩进（缩进深度用全局变量控制）。 3. 统计函数被调用的总次数（每次进入函数，无论是否计算，都算一次调用？注意：当使用记忆化时，虽然避免了重复计算，但是函数的调用仍然发生了，只是我们跳过了计算过程。根据样例输出，每次进入函数都算一次调用，包括被记忆化跳过的调用？） 注意样例输出： 输入0 4（不启用优化）: 调用了3次（f(4)进入两次f(3)，所以总共3次：f(4),f(3),f(3)） 输入1 4（启用优化）: 调用了3次（第一次f(4)调用，然后第一次f(3)是计算的，第二次f(3)是从记忆化中取的，但计入调用次数？因为第二次进入f(3)函数时，发现已经计算过，所以输出“calculated before”，并且计数一次） 因此，我们每次进入f函数，调用次数+1。即使是从记忆化中取，也计为一次调用。 具体步骤： 全局变量： long long memo[20]; // 记忆化数组，n的范围是3到13，所以数组大小20足够。初始化-1表示未计算。 int indent = 0; // 当前缩进深度（注意：每次递归调用会改变缩进，需要使用全局变量？但递归调用需要回溯，所以我们可以用局部变量传递，但这里缩进是全局的，而且输出要求是全局的缩进深度。但注意：多线程问题？但只有一个递归栈。所以我们可以用全局变量，但是每次进入函数增加，退出函数减少。注意：由于递归调用，可能会交错，所以缩进深度是全局的，但是我们必须保证每次进入和退出成对。 然而，题目要求：进入函数时输出一次，退出时输出一次。而递归调用中，同一个函数可能被多次调用，缩进深度应该反映当前的调用深度。所以我们可以用一个全局变量，但是注意在递归调用前增加缩进，递归调用后减少缩进。 但是，由于我们是在函数内部进行递归调用，我们可以这样： 函数开始：缩进深度增加，输出进入信息（但是注意，在输出进入信息时，缩进深度是当前的深度，然后深度+1） 函数结束：在返回前，缩进深度减少，输出退出信息（但是退出信息输出时的缩进深度是减少后的深度？） 题目要求： 进入函数f(n)时，先输出缩进（当前缩进空格个数），再输出"calculate begin f(n)"，然后缩进个数增加1。 退出时： 如果是计算结束：缩进个数先减少1（因为进入时增加了1，退出时要回到进入前的状态），然后输出缩进和"calculate end return f(n)=..." 如果是记忆化返回：缩进个数减少1，然后输出缩进和"calculated before return f(n)=..." 然而，这里有一个问题：在函数内部，我们可能会递归调用多次，每次递归调用都会改变全局缩进深度。因此，我们需要在函数开始的时候保存当前的缩进深度，然后在返回前恢复到这个深度？但题目要求是动态变化的。 实际上，我们可以这样设计： 使用全局变量indent表示当前的缩进深度。 在函数f(n)的开头： int current_indent = indent; // 保存当前的缩进深度，用于退出时恢复？但是不行，因为递归调用会改变全局indent。 另一种思路：我们不保存，而是按照如下步骤： 1. 输出当前缩进（indent个"| "）和进入信息。 2. 然后将indent加1。 3. 然后进行递归调用（在递归调用过程中，indent会继续增加）。 4. 在返回前，先将indent减1（因为进入时加了1，现在要退回），然后输出退出信息（此时缩进是indent减1后的值？实际上，退出信息输出的缩进应该是进入前的缩进深度，也就是我们输出进入信息时的缩进深度，而我们现在已经将indent减1了，所以输出退出信息时缩进深度正好是进入前的深度）。 但是，在记忆化返回的情况下，我们进入函数后，输出进入信息，然后发现已经计算过，那么我们需要： 先输出进入信息（缩进深度为indent），然后发现记忆化存在，那么就不需要计算，然后我们要输出退出信息（记忆化返回），这时缩进深度需要先减1？但是我们在进入时已经将indent加了1吗？还没有，因为按照步骤： 进入函数：先输出缩进（当前indent），然后输出进入信息，然后indent加1。 然后检查记忆化：发现已经计算过，那么我们就直接返回，但是返回前需要将indent减1（因为进入时加了1）？但是这样就会导致缩进深度在记忆化返回时也增加了1？所以我们需要减回去。 因此，无论是否记忆化，在进入函数时，我们都会先输出进入信息，然后indent++。然后在返回前（无论哪种返回）都要indent--，并输出相应的退出信息（除了记忆化返回，还有正常计算结束的返回）。 但是注意：在正常计算过程中，我们可能会递归调用其他函数，这些调用会改变indent。我们在递归调用结束后，需要将indent恢复到调用前的值吗？不需要，因为递归调用结束后，我们回到当前函数，当前函数的缩进深度应该是进入时的深度+1（因为进入时加了1）。而我们递归调用其他函数时，其他函数会改变indent，但是当其他函数返回时，它们会将自己的缩进深度减少（因为它们进入时加了1，退出时减了1），所以当我们递归调用返回后，当前的缩进深度应该是进入后加1的状态。 然后，在正常计算完成后，我们输出退出信息前，需要将缩进深度减1（为了回到进入前的深度），然后输出退出信息（此时缩进深度就是进入前的深度）。 所以，流程： void f(n): count++; // 全局调用次数统计 // 输出进入信息 print_indent(indent); printf("calculate begin f(%d)\n", n); indent++; // 进入函数，缩进加1 // 检查记忆化：如果启用优化且已经计算过 if (op == 1 && memo[n] != -1) { // 记忆化命中 long long ret = memo[n]; indent--; // 因为进入时加了1，现在要减回去 // 输出记忆化返回信息 print_indent(indent); printf("calculated before return f(%d) = %lld\n", n, ret); return ret; } // 正常计算 long long result; if (n == 3) { result = 1; } else { result = 0; for (int i=3; i<=n; i++) { if (i==3 || i==n) { result += f(n-1); } else { result += f(n-i+2) * f(i-1); } } } // 保存记忆化 if (op == 1) { memo[n] = result; } // 退出前：缩进减1，因为进入时加了1 indent--; // 输出正常计算结束的信息 print_indent(indent); printf("calculate end return f(%d) = %lld\n", n, result); return result; 但是，这里有一个问题：在正常计算过程中，我们递归调用了其他f函数，这些函数会改变全局的indent。当我们返回时，当前函数的缩进深度应该是进入时的深度+1（因为进入时加了1）吗？实际上，在整个计算过程中，递归调用其他函数后，其他函数会将自己的缩进深度恢复（因为它们进入时加1，退出时减1），所以当我们执行到循环结束（即计算完当前函数的result）后，全局的indent应该是等于当前函数进入后加1的值（因为当前函数进入时加了1，然后递归调用其他函数，其他函数会修改indent，但是其他函数返回后，indent会被它们恢复，所以当前函数的缩进深度还是进入后加1的状态）。 因此，在正常计算结束后，我们只需要将indent减1，然后输出退出信息。 但是，我们还需要注意：在递归调用的循环中，多次调用其他函数，这些函数会改变indent。所以我们必须保证在循环过程中，每次调用函数后，indent会恢复到调用前的值（即当前函数进入后加1的状态）？实际上，按照我们的设计，每个函数在返回前都会将indent减1（回到进入前的状态），所以当递归函数返回后，indent会回到调用它的函数中的状态（即调用前缩进深度+1？不对，应该是调用函数前的深度）。 举个例子： 假设当前函数f(4)进入时，缩进深度为0，然后输出进入信息，然后indent变成1。 然后调用f(3)： 进入f(3)：输出进入信息（缩进深度1），然后indent变成2。 然后计算f(3)=1，然后indent减1变成1，输出退出信息（缩进深度1），然后返回。 回到f(4)时，indent是1（因为f(3)退出时减了1，所以回到了f(4)进入后加1的状态，即1）。 然后f(4)继续循环，再次调用f(3)： 同样，f(3)进入：输出进入信息（缩进1），然后indent变成2；然后计算，然后退出时indent减1变成1，输出退出信息（缩进1）。 f(4)计算完毕，然后indent减1变成0，输出退出信息（缩进0）。 所以，这个设计是合理的。 但是，在记忆化的情况下，当我们调用f(3)时，第一次调用计算后，第二次调用时，f(3)内部会先输出进入信息（缩进1），然后发现记忆化命中，然后输出记忆化返回信息，并将indent减1（所以从2减到1），然后返回。这样回到f(4)时，indent还是1。 因此，全局变量count（调用计数）应该在每次进入函数时自增1（包括记忆化命中的情况）。 另外，注意缩进字符串是"| "（一个竖线加三个空格），重复indent次。 最后，在main函数中，我们读取op和n，然后初始化记忆化数组（全部设为-1），初始化缩进深度为0，调用计数为0（全局变量）。 然后调用f(n)，最后按要求输出答案和总调用次数。 注意：题目要求最后输出两行： "answer f(%d) = %lld\n" "total function invoked count = %lld\n" 但是，我们在函数调用过程中已经输出了递归过程，最后还要输出答案，而答案就是f(n)的返回值。 所以我们在main函数中： long long ans = f(n); printf("answer f(%d) = %lld\n", n, ans); printf("total function invoked count = %lld\n", count); 但是，注意：在递归过程中，我们可能会多次调用f，所以count在递归过程中已经累加。 另外，注意：记忆化数组memo需要初始化，而且由于n的范围是3到13，所以数组大小设为20即可。 但是，注意：在启用优化时，我们需要记忆化；不启用时，不需要记忆化。 但是，我们可以在不启用优化时也使用记忆化数组吗？题目要求：当op=1时启用优化。所以当op=0时，我们不使用记忆化数组（即即使数组有值也不使用，依然重新计算）。 因此，在函数中，我们判断记忆化的条件是：if (op==1 && memo[n]!=-1) 我们可以这样定义全局变量： int global_op; // 因为op在递归过程中不变，所以可以用全局变量传递。 或者将op作为参数传递，但是题目要求函数是f(int n)，所以不能改变函数参数。因此，我们使用全局变量。 所以，我们定义以下全局变量： int global_op; long long memo[20]; int indent = 0; long long count = 0; // 调用次数 然后，在f函数中： count++; // 每次进入函数，调用次数加1 ... 但是，题目要求函数名为f，所以我们需要修改原来的函数。 另外，注意：在循环中，递归调用f(n-1)和f(n-i+2)以及f(i-1)，这些调用都会改变全局变量（indent和count），所以我们的设计是可行的。 但是，注意：在递归调用中，我们可能会计算同一个函数多次（当op=0时）。而op=1时，我们会利用记忆化避免重复计算。 按照题目样例，我们写代码。 注意：缩进输出函数，我们可以写一个辅助函数，也可以直接循环输出。 例如： void print_indent(int level) { for (int i = 0; i < level; i++) { printf("| "); } } 但是，由于题目要求输出的是重复level次"| "，所以我们可以直接循环。 考虑到代码清晰，我们可以写一个函数，但是题目要求用C语言，我们也可以直接内嵌循环。 具体实现： 全局变量定义在函数外部。 由于题目要求输出调用过程，所以我们需要小心控制输出顺序。 我们按照上述思路编写代码。 注意：在函数开始，我们输出进入信息，然后indent++。 然后检查是否记忆化命中（如果启用优化且已经计算过），则返回记忆化的值（但是在此之前要输出记忆化返回信息，并调整缩进）。 否则，进行计算： 如果n==3，则结果=1。 否则，循环i从3到n，根据条件递归调用。 计算完成后，如果启用了优化，则保存结果到memo[n]。 然后，缩进减1，输出正常计算结束信息，返回结果。 但是，这里有一个问题：在递归调用的函数中，它们也会输出信息，所以整个输出是递归嵌套的。 我们按照样例4（0 5）来验证： 输入0 5，不启用优化。 输出样例4中，调用了9次函数。 注意：在循环中，我们调用了多次函数，这些函数的输出会嵌套在当前函数的输出中间。 所以，我们的代码结构如下： 全局变量： int global_op; long long memo[20]; int indent = 0; long long total_count = 0; // 总调用次数 函数f(n)的实现： total_count++; // 进入函数就计数 // 保存当前缩进？不需要，因为我们要立即输出进入信息 print_indent(indent); printf("calculate begin f(%d)\n", n); indent++; // 进入函数，缩进加1 if (global_op == 1 && memo[n] != -1) { // 记忆化命中 long long ret = memo[n]; indent--; // 因为前面加了1，这里要减回去 print_indent(indent); printf("calculated before return f(%d) = %lld\n", n, ret); return ret; } long long result; if (n == 3) { result = 1; } else { result = 0; for (int i = 3; i <= n; i++) { if (i == 3 || i == n) { result += f(n-1); } else { result += f(n-i+2) * f(i-1); } } } if (global_op == 1) { memo[n] = result; } indent--; // 退出函数前，缩进减1（恢复到进入前的缩进） print_indent(indent); printf("calculate end return f(%d) = %lld\n", n, result); return result; 在main函数中： int main() { int op, n; scanf("%d %d", &op, &n); global_op = op; // 初始化记忆化数组为-1 for (int i = 0; i < 20; i++) { memo[i] = -1; } indent = 0; total_count = 0; // 初始化计数器 long long ans = f(n); printf("answer f(%d) = %lld\n", n, ans); printf("total function invoked count = %lld\n", total_count); return 0; } 但是，这里有一个问题：在记忆化命中的情况下，我们返回了ret，但是函数最后还会执行后面的代码吗？不会，因为我们return了。所以上面的代码中，记忆化命中的代码块已经return了，不会执行后面的计算和退出信息（正常计算结束的退出信息）。 所以，上面的代码结构是正确的。 但是，我们还需要注意：在循环中递归调用时，递归调用会改变全局变量indent，但是当递归调用返回后，indent应该恢复到调用前的值（即当前函数进入后加1的状态）。而我们的设计保证了这一点：因为每个函数在退出时都会将indent减1（记忆化命中的函数也会减1），所以当递归调用返回后，indent会回到调用该递归函数之前的值（即当前循环时的缩进深度）。 因此，我们按照这个思路编写代码。 但是，注意：在递归调用过程中，可能会多次改变indent，所以我们必须保证在任何情况下（包括有return语句的分支）都正确地调整了indent。 在正常计算的分支中，我们在最后调整indent并输出结束信息。 在记忆化返回的分支中，我们在返回前调整indent并输出结束信息。 所以，不会出现缩进深度错误。 我们运行样例1：0 4 调用f(4): total_count=1, 输出"calculate begin f(4)"，缩进0，然后indent=1。 循环i=3: 进入if(i==3||i==n) -> true，调用f(3) 调用f(3): total_count=2, 输出"| calculate begin f(3)"（因为当前缩进是1，输出1个"| "），然后indent=2。 因为n==3，所以result=1。 然后indent减1变成1，输出"| calculate end return f(3)=1"（缩进1，即1个"| "）。 回到f(4)，此时indent=1（因为f(3)退出时减了1，所以回到1）。 循环i=4: 进入if(i==3||i==n) -> true，调用f(3) 调用f(3): total_count=3, 输出"| calculate begin f(3)"（缩进1），然后indent=2。 计算得到1，然后indent减1变成1，输出"| calculate end return f(3)=1"。 循环结束，result=1+1=2。 然后f(4)的indent减1变成0（因为进入时加了1），输出"calculate end return f(4)=2"（缩进0，即空）。 最后输出答案和总调用次数3。 符合输出样例1。 样例2：1 4 f(4): count=1，输出进入信息，缩进0，indent=1。 循环i=3：调用f(3) f(3): count=2，输出进入信息（缩进1），indent=2。 计算得到1，存入memo[3]=1（因为op=1），然后indent减1=1，输出结束信息（缩进1）。 f(4)得到1，result=1。 循环i=4：调用f(3) f(3): count=3，输出进入信息（缩进1），indent=2。 然后检查：op=1且memo[3]!=-1，所以命中。 然后indent减1变成1，输出记忆化返回信息（缩进1）并返回1。 result=1+1=2。 f(4)计算结束，存入memo[4]=2（op=1），然后indent减1=0，输出结束信息（缩进0）。 最后输出答案和总调用次数3。 符合输出样例2。 样例3和4比较复杂，但我们的逻辑应该一致。 但是，注意：在循环中，如果i在中间（不是3也不是n），那么我们要计算两个递归的乘积：f(n-i+2) * f(i-1) 例如：n=5, i=4（此时i不是3也不是5），那么就要计算 f(5-4+2)=f(3) 和 f(4-1)=f(3)的乘积。 所以样例3（1 5）： f(5)进入，输出进入信息（缩进0），indent=1。 i=3：条件成立，调用f(4) -> 注意：f(5)循环i从3到5。 进入f(4)（第一次调用f(4)）: count=2，输出进入信息（缩进1），indent=2。 f(4)循环： i=3：调用f(3)（第一次调用f(3)）: count=3, 输出进入信息（缩进2），indent=3。 f(3)=1，存入memo[3]=1，然后indent减1=2，输出结束信息（缩进2）。 i=4：调用f(3)（第二次调用f(3)）: count=4, 输出进入信息（缩进2），indent=3。 记忆化命中，输出记忆化返回信息（缩进2），indent减1=2，返回1。 所以f(4)=1+1=2，存入memo[4]=2，然后indent减1=1，输出结束信息（缩进1）。 回到f(5)，result += 2 （因为i=3时调用f(4)得到2）。 i=4：条件不成立（4不是3也不是5），所以计算 f(5-4+2)=f(3) 和 f(4-1)=f(3) 的乘积。 先调用f(3): count=5, 输出进入信息（缩进1），indent=2 -> 记忆化命中，输出记忆化返回信息（缩进1），返回1。 再调用f(3): count=6, 同样记忆化命中，输出记忆化返回信息（缩进1），返回1。 所以乘积=1*1=1，result=2+1=3。 i=5：条件成立，调用f(4)（第二次调用f(4)）: count=7, 输出进入信息（缩进1），indent=2。 记忆化命中（因为之前计算过f(4)），所以输出记忆化返回信息（缩进1），返回2。 所以result=3+2=5。 循环结束，f(5)=5，存入memo[5]（op=1），然后indent减1=0，输出结束信息（缩进0）。 总调用次数为7。 但是，输出样例3中，f(5)的调用过程如下： calculate begin f(5) | calculate begin f(4) | | calculate begin f(3) | | calculate end return f(3) = 1 | | calculate begin f(3) | | calculated before return f(3) = 1 | calculate end return f(4) = 2 | calculate begin f(3) | calculated before return f(3) = 1 | calculate begin f(3) | calculated before return f(3) = 1 | calculate begin f(4) | calculated before return f(4) = 2 calculate end return f(5) = 5 而我们上面的过程描述中，i=4时调用了两次f(3)，然后i=5时调用了一次f(4)。但是输出中，在i=4之后，输出的是： | calculate begin f(3) [这是第一个f(3)] | calculated before return f(3) = 1 | calculate begin f(3) [这是第二个f(3)] | calculated before return f(3) = 1 | calculate begin f(4) [这是f(4)的第二次调用] | calculated before return f(4) = 2 所以输出顺序和我们循环的顺序一致。 因此，我们按照上述代码实现。 注意：在循环中，递归调用的顺序就是循环的顺序。 另外，注意：在记忆化的情况下，我们保存了memo[n]，但是当op=0时，我们不使用记忆化，但是我们仍然会保存memo[n]（因为代码中在计算完成后，如果global_op=1才保存）。所以当op=0时，我们不保存，也不使用。 但是，为了避免混淆，我们可以将记忆化数组的初始化放在main函数中，并且当op=0时，我们也可以不初始化（但初始化了也没关系，因为不会使用）。 所以，我们编写代码。 注意：缩进字符串是"| "，每个缩进级别输出一次。 由于题目要求n最大为13，递归深度不会很深，所以不会出现栈溢出。 我们按照代码实现。 但是，注意：在函数f中，递归调用时，我们传递的是n-1, n-i+2, i-1。这些值可能小于3？题目保证n>=3，但是在递归调用中可能会出现小于3的情况吗？ 我们观察： 当n=3时，直接返回1，不会进入循环。 当n=4时：循环i从3到4。 当i=3：调用f(4-1)=f(3) -> 3>=3，没问题。 当i=4：调用f(4-1)=f(3) -> 没问题。 当n=5时：循环i从3到5。 i=3: 调用f(5-1)=f(4) -> 4>=3 i=4: 调用f(5-4+2)=f(3) 和 f(4-1)=f(3) -> 都是3 i=5: 调用f(5-1)=f(4) -> 4>=3 所以递归调用的参数不会小于3。但是，我们也要防止出现小于3的情况，因为题目只保证n>=3，而递归调用中，n-1最小为3? 当n=4时，n-1=3；当n=5时，n-1=4。而n-i+2：当i最大为n时，n-i+2=2（当i=n时，n-i+2=2）？不对，在循环中，当i=n时，我们进入的是if(i==3||i==n)分支，所以不会计算f(n-i+2)。而当i在中间时，i>=4且i<=n-1，所以n-i+2最小为：当i=n-1时，n-(n-1)+2=3。所以也不会小于3。 因此，我们不需要处理小于3的情况。 代码实现如下： </think>根据题目要求，我将实现一个带有记忆化优化和详细调用过程输出的递归函数。以下是完整的C语言解决方案： ```c #include <stdio.h> // 全局变量 int global_op; long long memo[20]; // 记忆化数组，n范围3-13，大小20足够 int indent = 0; // 当前缩进级别 long long total_count = 0; // 函数调用计数器 // 辅助函数：打印当前缩进 void print_indent(int level) { for (int i = 0; i < level; i++) { printf("| "); } } // 递归函数 long long f(int n) { total_count++; // 每次进入函数计数 // 打印函数开始信息 print_indent(indent); printf("calculate begin f(%d)\n", n); indent++; // 增加缩进级别 // 检查记忆化 if (global_op == 1 && memo[n] != -1) { long long ret = memo[n]; indent--; // 恢复缩进级别 print_indent(indent); printf("calculated before return f(%d) = %lld\n", n, ret); return ret; } long long result; // 基准情况 if (n == 3) { result = 1; } else { result = 0; // 循环计算 for (int i = 3; i <= n; i++) { if (i == 3 || i == n) { result += f(n - 1); } else { result += f(n - i + 2) * f(i - 1); } } } // 记忆化存储 if (global_op == 1) { memo[n] = result; } indent--; // 恢复缩进级别 print_indent(indent); printf("calculate end return f(%d) = %lld\n", n, result); return result; } int main() { int n; scanf("%d %d", &global_op, &n); // 初始化记忆化数组 for (int i = 0; i < 20; i++) { memo[i] = -1; // -1表示未计算 } indent = 0; total_count = 0; long long ans = f(n); // 输出最终结果 printf("answer f(%d) = %lld\n", n, ans); printf("total function invoked count = %lld\n", total_count); return 0; } ``` ### 代码解释 1. **全局变量**： - `global_op`: 存储是否启用优化的标志 - `memo[20]`: 记忆化数组，存储已计算的结果 - `indent`: 当前缩进级别，用于格式化输出 - `total_count`: 函数调用计数器 2. **缩进处理**： - `print_indent()`函数根据当前缩进级别打印相应数量的`| `字符串 - 进入函数时缩进级别+1，退出时-1，确保嵌套调用正确缩进 3. **递归函数f()**： - 每次进入函数时增加`total_count` - 打印开始信息，增加缩进级别 - 检查记忆化：如果启用优化且已计算过，直接返回结果并打印记忆化信息 - 递归计算： - n=3时直接返回1 - 否则通过循环计算，根据i值选择不同递归路径 - 计算结果后存储到记忆化数组（如果启用优化） - 打印结束信息，恢复缩进级别 4. **main函数**： - 读取输入参数op和n - 初始化记忆化数组为-1（未计算状态） - 调用递归函数并存储结果 - 输出最终答案和总调用次数 ### 优化效果分析 - **启用优化(op=1)**：通过记忆化避免重复计算，显著减少递归调用次数 - **禁用优化(op=0)**：每次调用都重新计算，递归次数呈指数级增长 - 示例中n=5时：启用优化调用7次，禁用优化调用9次 ### 时间复杂度 - 禁用优化：O(2^n)指数级 - 启用优化：O(n²)多项式级别 ### 空间复杂度 - O(n)用于存储记忆化结果和递归栈
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值