首先来讲一下数据结构中图的基本概念:
什么是图结构:
图数据结构是每个数据元素之间可以任意关联,构成了图结构。正是这种任意关联性,导致图结构中的数据关系的复杂性。
典型的图结构包含两个部分:
顶点(vertex): 图中的数据元素。
边(Edge):图中连接这些顶点的线。
所有的顶点构成一个顶点集合,所有边构成边集合,图结构就是由顶点集合和边集合组成。
无向图:
每条边都没有方向性,这种图称为无向图。
有向图:
每条边都有方向性,称为有向图。
顶点的度(Degree):
连接顶点的边的数量称为顶点的度。顶点的度在有向图和无向图中具有不同的意义。
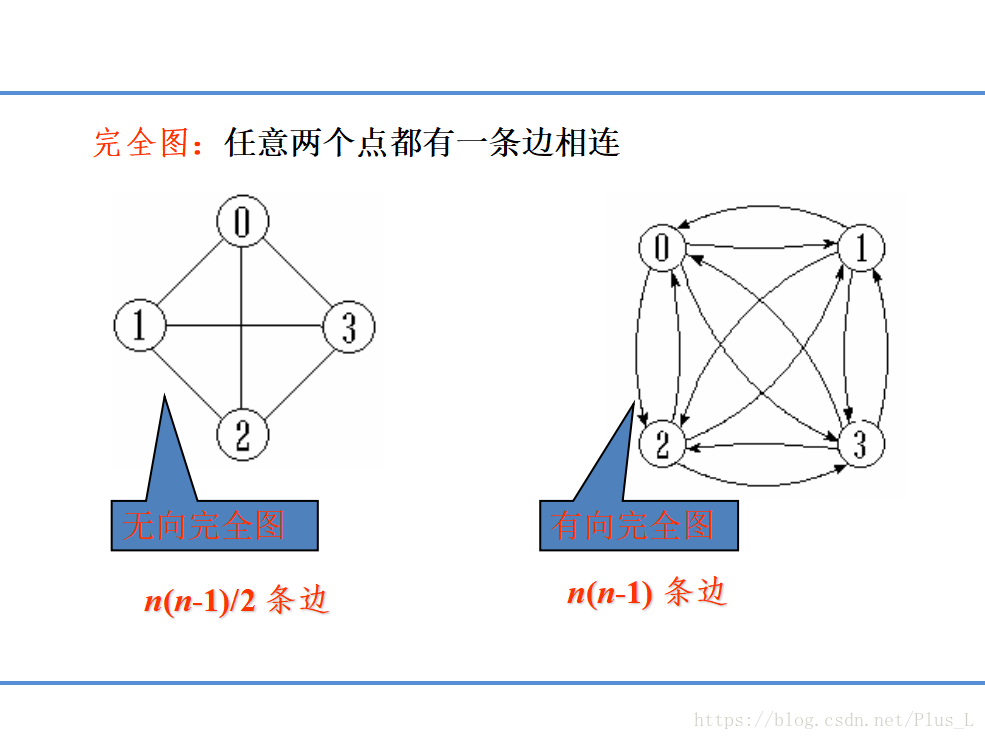
例如上图无向图的顶点 1 的度为 3 。
对于有向图则稍微复杂点,根据顶点的方向性,顶点有入度和出度之分:
入度是以该顶点为端点的入边数量,记为ID(V)例如:ID(0) = 3。
出度是以该顶点为端点的出边数量,记为OD(V)例如:OD(1) = 3。
邻接顶点:
邻接顶点是指图结构中一条边的两个顶点。无向图邻接顶点比较简单,在有向图中则意义不同。
有向图的入边邻接顶点:连接该顶点的边中的起始顶点。例如 <V0,V1>,V1是V0的入边邻接顶点。
有向图的出边邻接顶点:连接该顶点的边中的结束顶点。例如:<V1,V2>,V1是V2的出边邻接顶点。
图的顶点定义:
#include <iostream>
using namespace std;
#define MaxNum 20 //图的最大顶点数
#define MaxValue 65535 //最大值
typedef struct {
char Vertex[MaxNum]; //保存顶点信息
int GType; //图的类型
int VertexNum; //顶点的数量
int EdgeNum; //边的数量
int EdgeWeight[MaxNum][MaxNum]; //保存边的权
int isTrav[MaxNum]; //遍历标志
}GraphMatrix;
图的创建:
void CreateGraph(GraphMatrix *GM) //创建邻接矩阵图
{
int i, j, k;
int weight; //权
char EstartV, EendV; //边的起始顶点
cout << "输入图中各项顶点信息" << endl;
for (int i = 0; i < GM->VertexNum;i++) //输入顶点
{
getchar();
cout << "第" << i + 1 << "个顶点: " << endl;
cin >> GM->Vertex[i]; //保存到各顶点数组元素中
}
cout << "输入构成各边的顶点及权值:\n";
for (k = 0; k < GM->EdgeNum; k++)
{
getchar();
cout << "第" << k + 1 << "条边";
cin >> EstartV >> EendV >> weight;
for (i = 0; EstartV != GM->Vertex[i]; i++); //在已有顶点中查找始点
for (j = 0; EendV != GM->Vertex[j]; j++); //在已有顶点中查找终点
GM->EdgeWeight[i][j] = weight; //对应位置保存权值
if (GM->GType == 0) //若是无向图
GM->EdgeWeight[j][i] = weight; //在对角位置保存权值
}
}
清空图:
void ClearGraph(GraphMatrix *GM)
{
int i, j;
for (i = 0; i < GM->VertexNum; i++) //清空矩阵
{
for (j = 0;j < GM->VertexNum; j++)
{
GM->EdgeWeight[i][j] = MaxValue;
}
}
}
显示图:
void OutGraph(GraphMatrix *GM) //输出邻接矩阵
{
int i, j;
for (j = 0; j < GM->VertexNum; j++)
{
cout <<"\t"<< GM->Vertex[j]; //在第一行输出顶点信息
}
cout << endl;
for (int i = 0; i < GM->VertexNum; i++)
{
cout << GM->Vertex[i];
for (j = 0; j < GM->VertexNum; j++)
{
if (GM->EdgeWeight[i][j] == MaxValue) //若权值为最大值
{
cout << "\t Z"; //用Z表示无穷大
}
else
{
cout <<"\t"<<GM->EdgeWeight[i][j]; //输出边的权值
}
}
cout << endl;
}
}
遍历图:
1.首先,从数组中isTrav中选择一个未被访问的顶点V,将其标记为1,表示已访问。
2.接着,从Vi的一个未被访问过的邻接顶点出发进行深度优先遍历。
3.重复 步骤2,直至图中所有和Vi路径相通的顶点都被访问过。
4.重复步骤3,直至所有顶点都被访问。
void DeepTraOne(GraphMatrix *GM,int n)
{
int i;
GM->isTrav[n] = 1; //标记改顶点已处理过
cout << " " << GM->Vertex[n]; //输出结点数据
//添加处理节点的操作
for (i = 0; i < GM->VertexNum; i++)
{
if (GM->EdgeWeight[n][i] != MaxValue && !GM->isTrav[n])
{
DeepTraOne(GM, i); //递归进行遍历
}
}
}
//深度优先遍历
void DeepTraGraph(GraphMatrix *GM)
{
int i;
for (i = 0; i < GM->VertexNum; i++) //清除各顶点遍历标志
{
GM->isTrav[i] = 0;
}
cout << "深度优先遍历节点: ";
for (int i = 0; i < GM->VertexNum; i++)
{
if (!GM->isTrav[i]) //若该顶点未遍历
{
DeepTraOne(GM, i); //调用函数进行遍历
}
}
cout << endl;
}
main函数:
int main()
{
GraphMatrix GM;
cout << "输入生成图的类型: ";
cin >> GM.GType;
cout << "输入图的顶点数量: ";
cin >> GM.VertexNum;
cout << "输入图的边的数量: ";
cin >> GM.EdgeNum;
ClearGraph(&GM);
CreateGraph(&GM);
cout << "该图的邻接矩阵数据如下: " << endl;
OutGraph(&GM);
DeepTraGraph(&GM);
system("pause");
return 0;
}
测试输出:
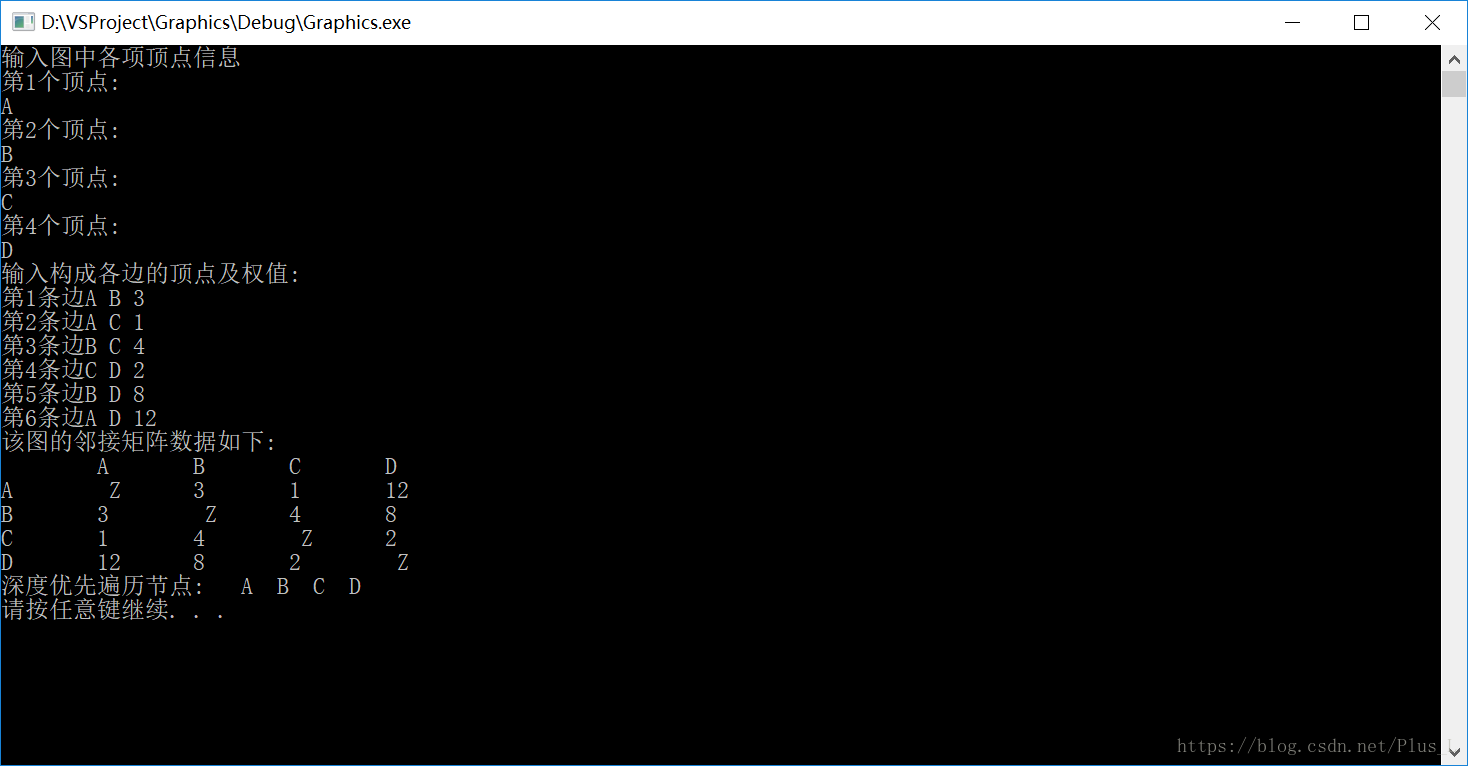







 本文深入讲解了图数据结构的基本概念,包括无向图和有向图的区别,顶点的度、入度和出度的概念,以及邻接顶点的定义。同时,提供了C++代码示例,展示了如何创建图结构,进行深度优先遍历,以及如何实现图的显示和清空操作。
本文深入讲解了图数据结构的基本概念,包括无向图和有向图的区别,顶点的度、入度和出度的概念,以及邻接顶点的定义。同时,提供了C++代码示例,展示了如何创建图结构,进行深度优先遍历,以及如何实现图的显示和清空操作。
















 8202
8202

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








