树及二叉树的定义与前中后序遍历

树的定义：

树(Tree)是n(n >= 0)个结点的有限集，它或为空树(n = 0);或为非空树，对于非空树T:

1.有且仅有一个根节点。

2.除根节点以外的其余节点可以分为m (m > 0)个互不相交的有限集 T1,T2,T3,...,Tm,其中每一个集合本身又是一棵树，并且称为根的子树。

 

 

树的一些基本名词，术语：

根：根节点，没有直接前驱

叶子：终端节点，没有后继

森林：m棵不相交的树的集合

节点：树的数据元素

节点的度：节点挂接的子树数

节点的层次：从根节点到该节点的层数

树的度：所有节点度中的最大值

树的深度：所有节点中最大的层数（也称为树的高度)

二叉树定义:

二叉树（binary tree）是 n (n >= 0) 个节点所构成的集合，它或为空树 （n = 0）；或为非空树，对于非空树T：

1.有且仅有一个根节点。

2.除根节点以外的其余节点分为两个互不相交的子集T1 和 T2，分别称为T的左子树和右子树，且T1和T2本身又是二叉树。

 

二叉树的性质：

1.一棵非空二叉树的第i层最多有2^i+1个节点（i>1)。

2.深度为 k 的非空二叉树最多有 2^k-1个节点。

3.若非空二叉树有 n0 个叶节点，有 n2 个度为2的节点，则    n0 = n2 + 1。

4.具有 n 个节点的完全二叉树的深度 k = (log2n) +  1。

 

二叉树的基本特点：

 

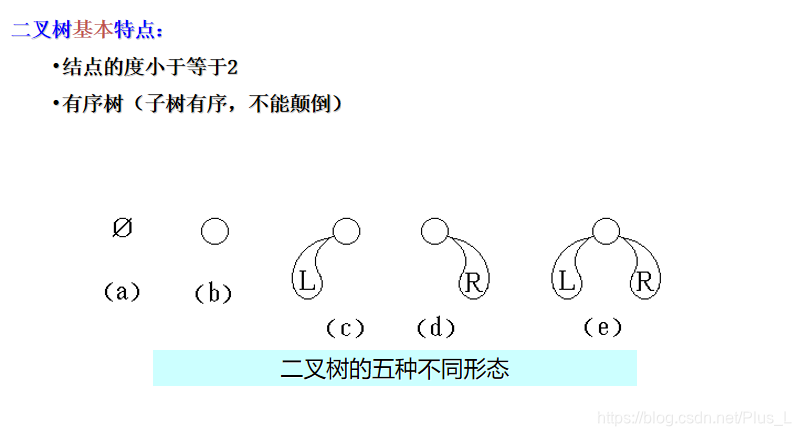
完全二叉树和满二叉树：

 

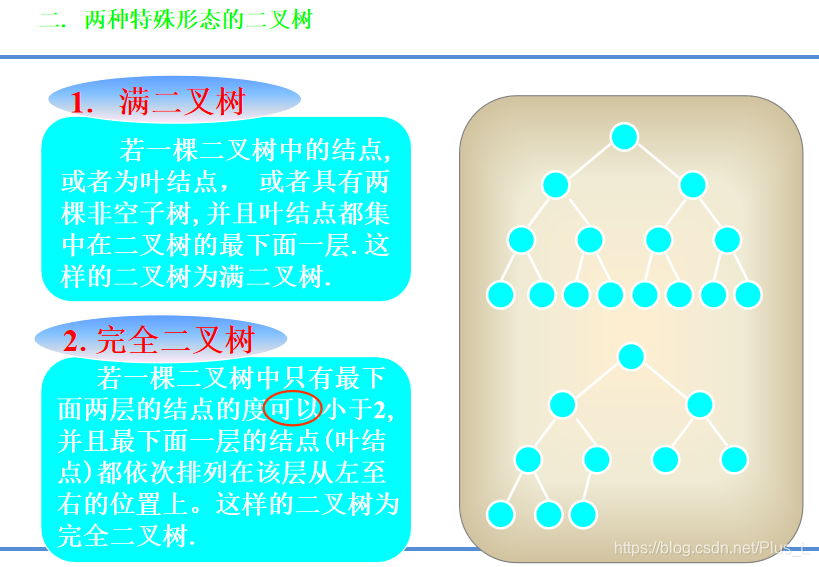
一般二叉树的顺序存储:

 

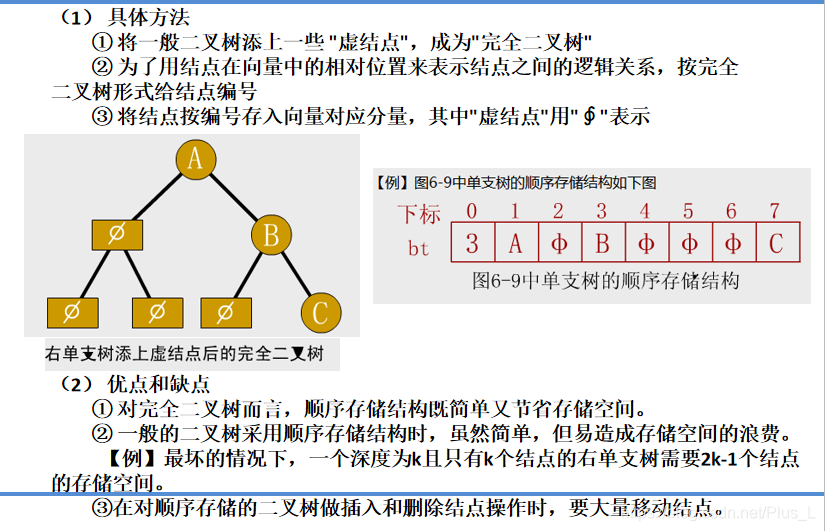
 二叉树链式存储:

 

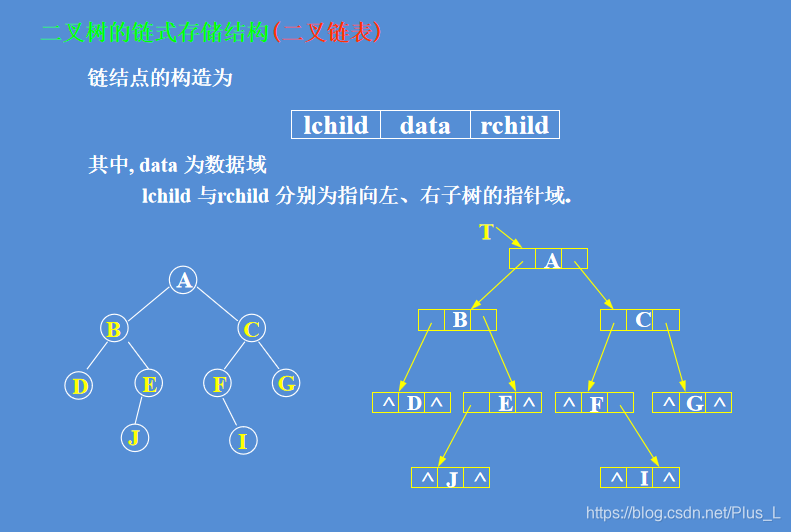
遍历的基本概念：

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。    

遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

 1．遍历方案     从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作：  

（1）访问结点本身(N)，    

（2）遍历该结点的左子树(L)，    

（3）遍历该结点的右子树(R)。

以上三种操作有六种执行次序：

    NLR、LNR、LRN、NRL、RNL、RLN。  

注意：    

     前三种次序与后三种次序对称，故只讨论先左后右的前三种次序。

 

先序遍历：

若二叉树非空：

1.访问根节点。

2.遍历左子树。

3.遍历右子树。

 

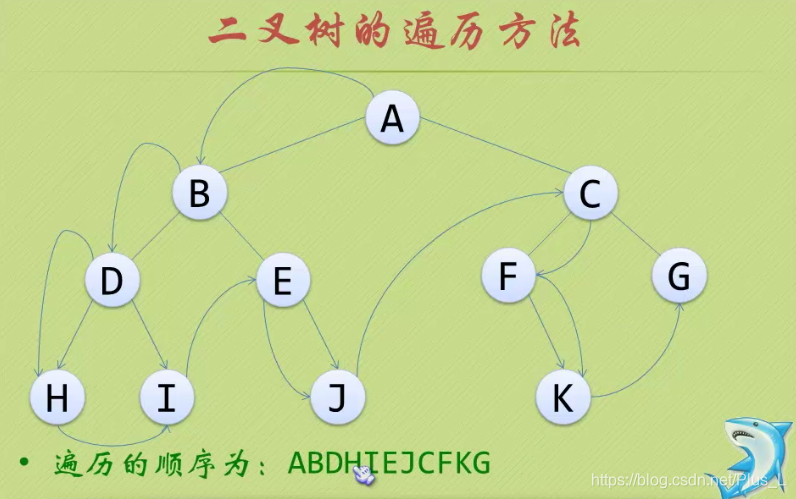
中序遍历：

若二叉树非空：

1.遍历左子树。

2.遍历根节点。

3.遍历右子树。

 

typedef char TElemType;

typedef enum PointerTag{Link,Thread};

typedef struct ThrBiNode{
	TElemType data;
	ThrBiNode *lchild, *rchild;  // 左右孩子指针
	PointerTag lTag, RTag;    // 左右指示
}ThrBiNode, *ThrBiTree;

// 中序遍历进行中序线索化（左 根 右）
void InThreading(ThrBiTree T, ThrBiTree &pre)
{
	if (T){
		InThreading(T->lchild, pre);   // 左子树线索化

		if (!T->lchild){
			// 当前结点的左孩子为空
			T->lTag = Thread;
			T->lchild = pre;
		}
		else
		{
			T->lTag = Link;
		}

		if (!pre->rchild){
			// 前驱结点的左孩子为空
			pre->RTag = Thread;
			pre->rchild = T;
		}
		else
		{
			pre->RTag = Link;
		}
		pre = T;
		InThreading(T->rchild, pre);   // 右子树线索化
	}
}

// 中序遍历二叉树T，并将其中序线索化，Thrt指向头结点
void InOrderThreading(ThrBiTree T, ThrBiTree &Thrt)
{
	// 初始化线索链表，为建立一个头结点
	Thrt = (ThrBiTree)malloc(sizeof(ThrBiNode));
	Thrt->lTag = Link;
	Thrt->RTag = Thread;
	if (!T)    // 如果二叉树为空树，则Thrt->lchild指针回指
	{
		Thrt->lchild = Thrt;
		Thrt->rchild = Thrt;
	}
	else
	{
		Thrt->lchild = T;
		ThrBiNode *pre = Thrt;   // pre指针总指向当前结点的前驱结点
		InThreading(T, pre);
		// 继续为最后一个结点加入线索
		pre->RTag = Thread;  
		pre->rchild = Thrt;// 最后一个结点的rchild域指针回指
		Thrt->rchild = pre;  // 头结点的rchild域指针指向最后一个结点
	}
}

// 中序遍历打印二叉线索树T（非递归算法）,T指向头结点，头结点的lchild链域指向二叉树的根结点
void InOrderTraversePrint(ThrBiTree T)
{
	ThrBiNode *p = T->lchild;  // p指向根结点
	while (p != T)  // 空树 或遍历结束 p==t
	{
		while (p->lTag == Link)
			p = p->lchild;	

		// 此时p指向中序遍历序列的第一个结点（最左下的结点）
		printf("%c ", p->data);  // 打印其左子树为空的结点

		while (p->RTag == Thread && p->rchild != T)
		{
			p = p->rchild;
			printf("%c ", p->data);   // 访问后续结点
		}
		p = p->rchild;

	}
	printf("\n");
}

// 利用先序序列建立一颗二叉树，'.'代表空树
// 测试数据：abc..de.g..f...#
void CreateBiTreePreOrder(ThrBiTree &T)
{
	char ch;
	scanf("%c", &ch);
	if (ch != '#')
	{
		if (ch == '.'){
			T = NULL;
		}
		else
		{
			T = (ThrBiNode*)malloc(sizeof(ThrBiNode));
			T->data = ch;
			CreateBiTreePreOrder(T->lchild);
			CreateBiTreePreOrder(T->rchild);
		}
	}
}

int main(int argc, char* argv[])
{
	ThrBiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	CreateBiTreePreOrder(T);  // 建立二叉树

	ThrBiTree Thrt;
	InOrderThreading(T, Thrt); // 将二叉树T中序线索化

	// 中序遍历二叉线索树
	InOrderTraversePrint(Thrt);

	return 0;
}

 

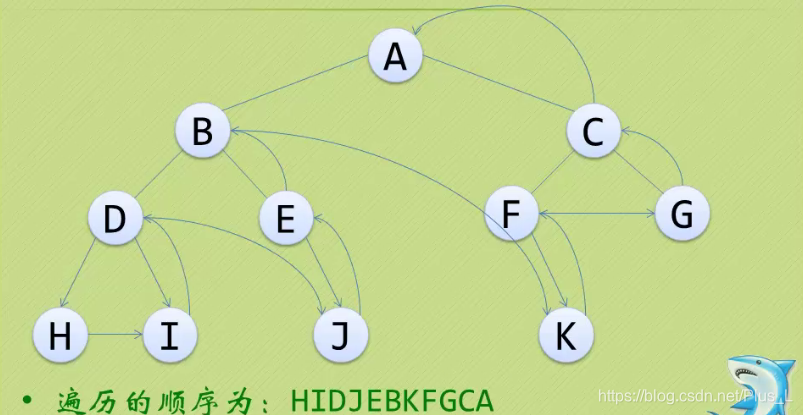
后序遍历：

若二叉树非空:

1.遍历左子树。

2.遍历右子树。

3.遍历根节点。