硅基计划4.0 算法二叉树深搜(DFS)

最新推荐文章于 2025-12-17 20:27:06 发布

原创最新推荐文章于 2025-12-17 20:27:06 发布 · 1k 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #leetcode #剪枝 #java #数据结构

1752388689910

文章目录

一、计算布尔二叉树的值

题目链接
这里，题目给了我们值，我们要自己转换成一棵真正的布尔二叉树
我们对于每一个子树的根节点，我们需要知道其左右子树的布尔值，然后再根据当前子树的根节点值进行判断，向上返回结果
这不就是一个后序遍历吗，直接

boolean left = dfs(root.left);
boolean right = dfs(root.right);
2-->||-->left||right,3-->&&-->left&&right

递归出口就是当我们遇到叶子节点，直接返回叶子节点的值然后判断是要返回true还是false

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean evaluateTree(TreeNode root) {
        if(root.left == null){
            return root.val == 0 ? false : true;
        }
        boolean left = evaluateTree(root.left);
        boolean right = evaluateTree(root.right);
        return root.val == 2 ? left || right : left && right;
    }
}

二、求根节点到叶子节点的数字之和

题目链接
注意，这一题中每一条路径上的数字都是有位数的，因此我们可能需要一个全局变量记录
我们可以这么想，既然我们递归的时候每一条路径都要遍历到
那么我们可以搞一个全局变量value写在方法参数那里，用来记录从最开始的根节点到当前根节点路径上的数字之和
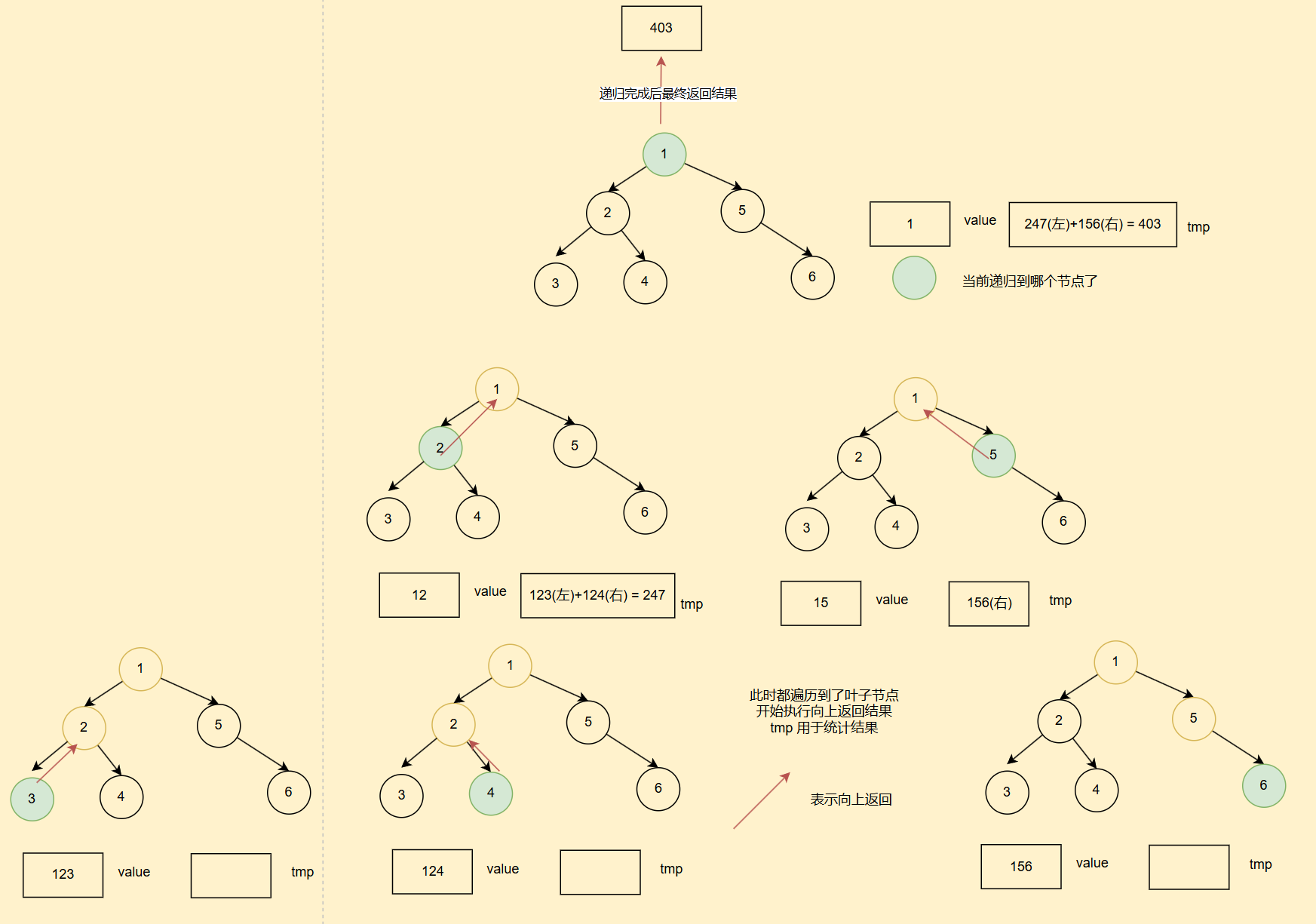
然后我们方法内部再搞一个临时变量tnp，用来接收从叶子节点返回的结果
我们递归的出口就是遇到叶子节点，直接返回我们之前设定好的全局变量value的值就好了，那么我们这一条路径上的值就求完了
先写个伪代码

dfs(root,value){
    value = value * 10+root.val;
    //判断叶子节点
    return value;
    //临时变量
    int tmp = 0;
    root.left != null --> tmp += root.left;
    root.right != null --> tmp += root.right;
    //返回
    return tmp;
}

我们直接画图来讲解

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumNumbers(TreeNode root) {
        return sumNumbersChild(root,0);
    }

    private int sumNumbersChild(TreeNode root,int value){
        //value用于表示在遇到叶子节点后返回这个路径上的值
        //tmp用于统计每一条叶子节点路径上的值，进行求和，返回上一级节点
        value = value*10 + root.val;
        //遇到叶子节点
        if(root.left == null && root.right == null){
            //遇到叶子节点返回这个路径上的值
            return value;
        }
        int tmp = 0;
        if(root.left != null){
            //每次深度递归都要传入当前路径上的值
            tmp += sumNumbersChild(root.left,value);
        }
        if(root.right != null){
            tmp += sumNumbersChild(root.right,value);
        }
        return tmp;
    }
}

三、二叉树剪枝——决策树

题目链接
这一题题目意思就是要把值为0的子树剪去
我们对于每一个节点，如果左子树是需要剪去的树，右子树也是需要剪去的树
那么当前根节点的子树需要剪去吗
不一定，虽然我左右子树都是0（即需要剪去的树），但是我当前根节点的值不为0，那么当前根节点就要保留
要做到这一点，我们可以进行后序遍历的DFS
先正常递归，即root.left = dfs(root.left),root.right = dfs(root.right)
然后再判断左右子树是不是需要剪去的树，并且再判断当前根节点值是否为0
如果是0，就把当前根节点置为null，然后直接返回root
反之不用置null，直接向上返回

对于递归出口，如果遇到叶子节点，因为左右子树都是空树，不需要判断了，仅需判断当前叶子节点的值是否是0，是0就置null然后向上返回，不是就直接向上返回

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode pruneTree(TreeNode root) {
        if(root == null){
            return null;
        }
        root.left = pruneTree(root.left);
        root.right = pruneTree(root.right);
        if(root.left == null && root.right == null && root.val == 0){
            root = null;
        }
        return root;
    }
}

四、验证二叉搜索树

题目链接
还记得我们之前讲过二叉搜索树中序遍历的结果是一个升序的数组吗
我们利用这个特性，对其进行中序遍历，判断就好了

但是，难道需要把整棵树遍历完后，根据结果的数组再去一个个比较吗，未免太麻烦了
因此我们可以定义一个全局变量preV，这个遍历意义就在于保存中序遍历时，在当前节点的前一个节点的值
然后我们根据这个值去比较，如果当前根节点值大于prev，说明是正确的，因为中序遍历结果是一个升序排序的数组
反之如果是小于等于preV，我们直接返回false

好，现在我们讲宏观的递归过程
对于每一个节点，如果左子树不是二叉搜索树
那么整棵树就一定不是一棵二叉搜索树，我们直接return false达到左子树剪枝的目的，减少递归次数，优化代码执行效率
同样对于右子树，如果不是一棵二叉搜索树，直接return false达到右子树剪枝的目的
最后再判断根节点，这就是我们刚刚讲的根节点判断
如果根节点是符合的，记住要把preV = root.val，好让下一次比较能够正确地进行

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    long preV = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root == null){
            //空节点默认是二叉搜索树
            return true;
        }
        boolean left = isValidBST(root.left);
        //如果左子树本身就不是搜索树，直接返回
        if(!left){
            return false;
        }
        boolean current = true;
        //验证当前根节点是否符合特征，因为二叉搜索树的中序遍历是升序
        //因此理应当前根节点的值要大于前驱节点的值
        if(root.val <= preV){
            current = false;
        }
        //如果当前根节点也不是搜索树，也是直接返回
        if(!current){
            return false;
        }
        //如果符合要求，我们修改前驱节点的值，再去右子树看看
        preV = root.val;
        boolean right = isValidBST(root.right);
        //因为之前左子树禾根节点都判断了，此时只需要看看右子树是不是符合要求就好了
        return right;
    }
}

五、二叉搜索树中第K小的元素

题目链接
这一题就是我们讲数据结构的时候的TopK问题，我们跟刚刚那一题一样，弄一个全局变量
进行中序遍历，如果遍历到当前根节点的时候，就是第K个元素，我们直接返回结果就好了

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int count = 0;
    int ret = 0;
    public int kthSmallest(TreeNode root, int k) {
        count = k;
        kthSmallestChild(root);
        return ret;
    }

    //中序遍历
    private void kthSmallestChild(TreeNode root){
        if(root == null || count == 0){//剪枝
            return;
        }
        kthSmallestChild(root.left);
        //遍历到当前根节点才算一个
        count--;
        if(count == 0){
            //如果count==0直接返回，不用继续递归了
            ret = root.val;
            return;
        }
        kthSmallestChild(root.right);
    }
}

六、二叉搜索树所有路径

题目链接
这一题大家不会觉得和我们的第二题很像吗，只不过不是计算值，而是统计value
对于每一个节点，添加当前根节点数值后，需要加上->，然后递归左右子树
如果是叶子节点，添加当前根节点值后，不需要再添加上->，添加结果，直接回溯

我们可以在参数中定义一个变量paths，用来记录从根节点到当前节点的路径上的数字
对于每一个方法体内部，我们再定义一个临时变量path，然后去递归左右子树

我们还可以采用剪枝策略进一步优化代码，如果左子树是空子树，不需要递归，同理右子树是空子树也不需要递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<String> list;
    public List<String> binaryTreePaths(TreeNode root) {
        list = new ArrayList<>();
        binaryTreePathsChild(root,new StringBuilder());
        return list;
    }

    private void binaryTreePathsChild(TreeNode root,StringBuilder paths){
        //每一层的StringBuilder，然后paths是上一层的变量
        //我们要基于前面的路径创建当前层的字符串
        StringBuilder path = new StringBuilder(paths);
        path.append(root.val);
        if(root.left == null && root.right == null){
            list.add(path.toString());
            return;
        }
        path.append("->");
        if(root.left != null){
            binaryTreePathsChild(root.left,path);
        }
        if(root.right != null){
            binaryTreePathsChild(root.right,path);
        }
    }
}

七、全排列

题目链接
对于这种复杂问题，我们可以通过绘制决策树来编写代码

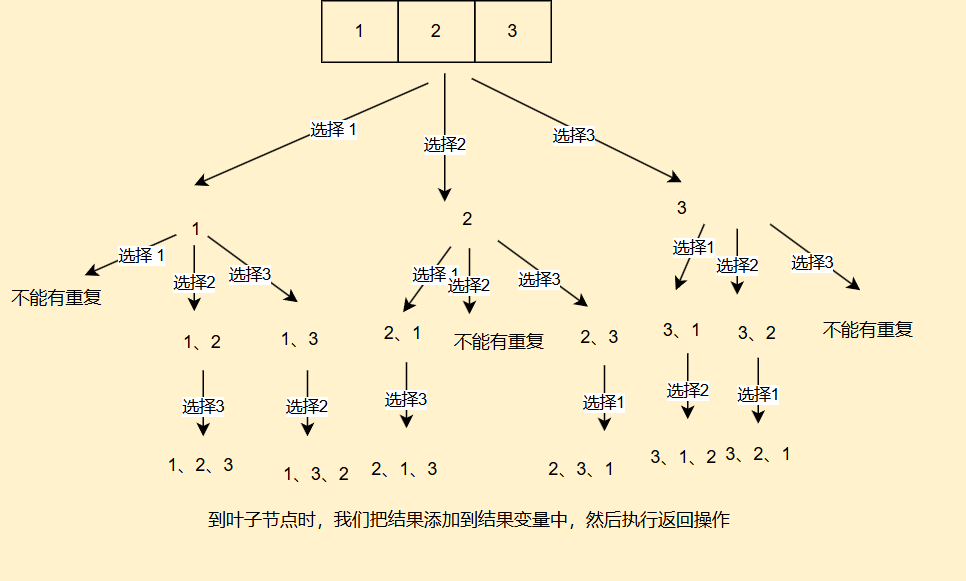
因此，我们需要两个全局变量，一个用来存放结果，一个用来标记路径
记得再向上回溯到时候，要恢复成上一个节点的路径，因此需要把末尾元素删除

接下来再说说如何剪枝，即如何选择不重复的元素，这就需要我们再定义一个全局变量boolean [] isChoic
只要这个数字被选择一次，我们就把这个数字看成这个数字下标，然后把isChoic[下标] = true就好

在后续递归的时候，如果这个数已经被选择过了，就直接跳过，否则我们就进行添加数字-->isChoic置为true-->递归-->恢复现场
最后在恢复现场（回归）的时候，要重新置为false，因为你还要递归其他数啊
比如你先递归1,1回溯后你还要递归2，但是假如2你刚刚没有置为false，就会导致2的情况被全部忽略
即回溯到最上面一层的时候，要使得其他数都是默认没有被选择过的

class Solution {
    List<List<Integer>> list;//结果
    List<Integer> path;//路径记录
    boolean [] isUse;//数字是否使用
    public List<List<Integer>> permute(int[] nums) {
        list = new ArrayList<>();
        path = new ArrayList<>();
        int length = nums.length;
        isUse = new boolean[length];
        searchPermutations(nums);
        return list;
    }

    private void searchPermutations(int [] nums){
        if(path.size() == nums.length){
            //递归出口，path始终变化，因此我们每次添加需要保留当前路径
            list.add(new ArrayList<>(path));
            return;
        }
        //遍历数组
        for(int i = 0;i < nums.length;i++){
            //没有出现过的数字才能加入顺序表中
            if(!isUse[i]){
                path.add(nums[i]);
                isUse[i] = true;//使用后记录
                searchPermutations(nums);
                isUse[i] = false;//重新设置为默认值
                path.remove(path.size()-1);//回溯剪枝
            }
        }
    }
}

八、子集

题目链接

1. 一般解法

我们先讲一个常见的解法，我们先绘制决策树

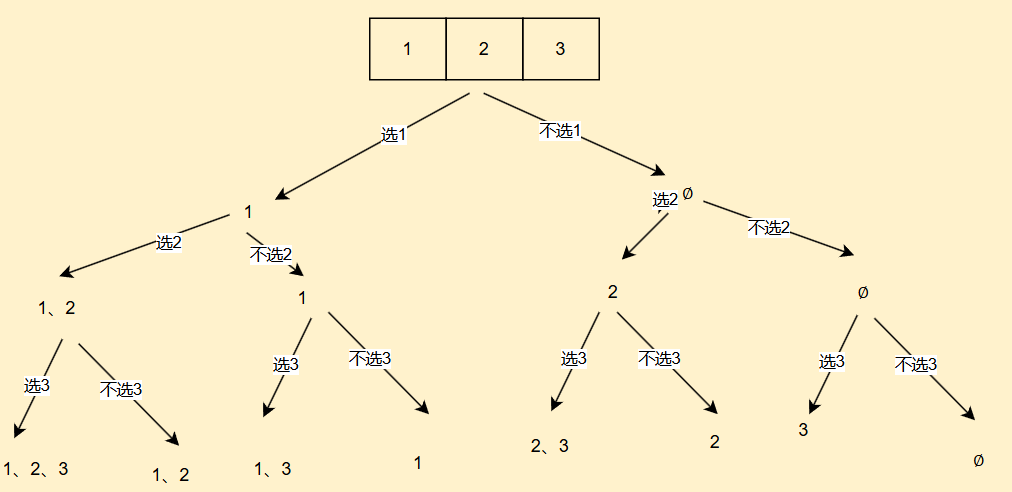
通过上面决策树，不难理解，最后的结果都在叶子节点
我们定义一个全局变量path去记录路径，再定义结果变量用于保存结果
对于函数参数，首先是数组本体，其次是下标
为什么是下标，因为我们每一次选择的时候，是根据下标位置选择值的
即如果我们这个数已经选择了，我们递归的时候下标就要往后走一位
否则就保持不变
递归出口就是当我们下标越界的时候，就是出口，此时我们添加结果
不要忘了，我们全局变量path在回溯的时候需要恢复现场，要把末尾元素去掉

class Solution {
    List<List<Integer>> list;
    List<Integer> path;
    public List<List<Integer>> subsets(int[] nums) {
        list = new ArrayList<>();
        path = new ArrayList<>();
        subsetsChild(nums,0);
        return list;
    }

    private void subsetsChild(int [] nums,int pos){
        if(pos == nums.length){
            list.add(new ArrayList(path));
            return;
        }
        //选择
        path.add(nums[pos]);
        subsetsChild(nums,pos+1);
        path.remove(path.size()-1);//回溯删除

        //不选择
        subsetsChild(nums,pos+1);
    }
}

2. 巧妙解法

我们刚刚是根据选不选择去决定每一棵子树的走向
那现在，我们可以根据元素个数决定我们的子树走向
每次选择都是选择当前下标之后的元素！！
老样子我还是绘制决策树进行演示

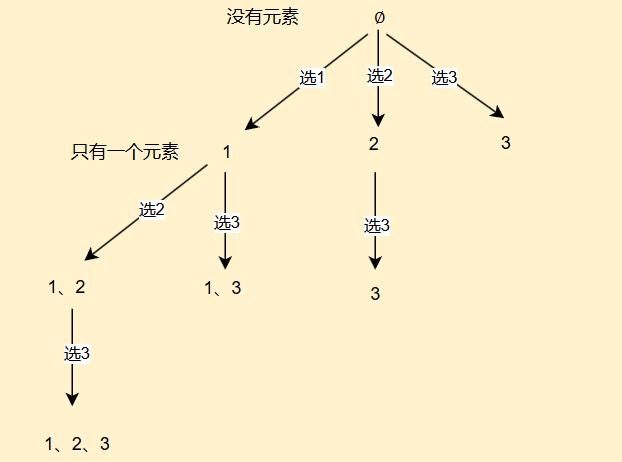
你会观察到这棵决策树非常简洁，而且自带剪枝，优化后效率极高
并且每一层每一个节点都是我们想要的结果

因此我们还是需要一个全局变量path，还是需要一个结果变量保存结果
再回溯的时候还是需要恢复现场，把最后一个元素去掉
但是每一次枚举都是从当前下标往后枚举

因为我们每一个节点都是结果，因此我们不需要出口，只需要一个循环限制一下下标的边界就好

class Solution {
    List<List<Integer>> list;
    List<Integer> path;
    public List<List<Integer>> subsets(int[] nums) {
        list = new ArrayList<>();
        path = new ArrayList<>();
        subsetsChild(nums,0);
        return list;
    }

    private void subsetsChild(int [] nums,int pos){
        list.add(new ArrayList(path));
        for(int i = pos;i < nums.length;i++){
            path.add(nums[i]);
            subsetsChild(nums,i+1);
            //回溯，即恢复现场
            path.remove(path.size()-1);
        }
    }
}