【IQA技术专题】梯度幅值IQA：GMSD

本文将围绕《GMSD: Gradient Magnitude Similarity Deviation: An Highly Efficient Perceptual Image Quality Index》展开完整解析。GMSD实现的是有参考的图像质量评价指标，可以有效地对图像的感知（Fidelity）质量进行评估。参考资料如下：
[1]. 论文地址
[2]. 代码地址

---

专题介绍

图像质量评价（Image Quality Assessment, IQA）是图像处理、计算机视觉和多媒体通信等领域的关键技术之一。IQA不仅被用于学术研究，更在影像相关行业内实现了完整的商业化应用，涉及影视、智能手机、专业相机、安防监控、工业质检、医疗影像等。IQA与图像如影随形，其重要程度可见一斑。

但随着算法侧的能力不断突破，AIGC技术发展火热，早期的IQA或已无法准确评估新技术的能力。另一方面，千行百业中各类应用对图像质量的需求也存在差异和变化，旧标准也面临着适应性不足的挑战。

本专题旨在梳理和跟进IQA技术发展内容和趋势，为读者分享有价值、有意思的IQA。希望能够为底层视觉领域内的研究者和从业者提供一些参考和思路。

系列文章如下：
【1】🔥IQA综述
【2】PSNR&SSIM
【3】Q-Insight
【4】VSI
【5】LPIPS
【6】DISTS
【7】Q-align

---

一、研究背景

IQA研究者在当时已经意识到PSNR等像素级别的指标，无法很好的在“感知”级别上对图像质量做有效的评估。现有 FR-IQA 模型（如 FSIM）虽精度高，但计算复杂；部分模型（如 SSIM）虽然计算简单，但精度不够。作者想要提出兼具高预测精度和高计算效率的 FR-IQA 模型。
总结该论文结构如下：

二、GMSD方法

2.1 实验发现

与VSI相似，作者针对不同的退化用自己提出的指标做了一个实验，如下所示，摘取了其中一个退化类型。

其中，r和d分别是参考图和退化图，${\text{m}}_{\text{r}}$与${\text{m}}_{\text{d}}$分别是作者提出的梯度幅值指标所计算的梯度幅值图，GMS是两幅梯度幅值图的相似度，灰度值越大代表着越相似。从中可以看到图像梯度对失真敏感，不同局部结构的失真程度不同，全局变化可反映整体质量。

2.2 方法总览

方案如下所示：

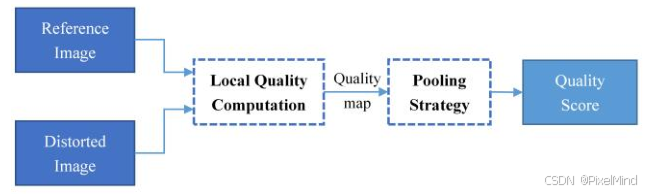
可以看到流程比较清晰，分为两个子部分：

1. Local Quality Computation：用于描述局部区域的质量，使用 3×3 Prewitt 滤波器来进行提取，公式如下所示。$${\mathbf{h}}_x=\left[\begin{array}{ccc}1/3& 0& -1/3\\ 1/3& 0& -1/3\\ 1/3& 0& -1/3\end{array}\right],{\mathbf{h}}_y=\left[\begin{array}{ccc}1/3& 1/3& 1/3\\ 0& 0& 0\\ -1/3& -1/3& -1/3\end{array}\right]$$提取完x和y方向的梯度后，使用以下公式，获取梯度幅值。$$\begin{gathered} {\mathbf{m}}_r(i)=\sqrt{(\mathbf{r}\otimes {\mathbf{h}}_x{)}^2(i)+(\mathbf{r}\otimes {\mathbf{h}}_y{)}^2(i)} \\ {\mathbf{m}}_d(i)=\sqrt{(\mathbf{d}\otimes {\mathbf{h}}_x{)}^2(i)+(\mathbf{d}\otimes {\mathbf{h}}_y{)}^2(i)} \end{gathered}$$${\text{m}}_{\text{r}}$与${\text{m}}_{\text{d}}$分别是参考图和退化图的梯度幅值。最后再计算相似度就可以得到局部的质量估计了。$$GMS(i)=\frac{2{\mathbf{m}}_r(i){\mathbf{m}}_d(i)+c}{{\mathbf{m}}_r^2(i)+{\mathbf{m}}_d^2(i)+c}$$其中$c$是一个用于稳定数值的常数。

2. Pooling Strategy：使用radient Magnitude Similarity Deviation (GMSD)方法来进行池化提取全局图像质量分数。计算过程中会使用到Gradient Magnitude Similarity Mean (GMSM)，两者的公式表示如下：$$GMSM=\frac{1}{N}\sum _{i=1}^{N}GMS(i)$$ $$GMSD=\sqrt{\frac{1}{N}\sum _{i=1}^N(GMS(i)-GMSM{)}^2}$$作者这里还给出了GMSD相较GMSM的优势，比如说下图：
   
   其中(a) 原始图像 “Fishing”、其受高斯噪声污染的版本（DMOS = 0.4403；GMSM = 0.8853；GMSD = 0.1420 ）以及它们的梯度相似图。(b) 原始图像 “Flower”、其模糊版本（DMOS = 0.7785；GMSM = 0.8745；GMSD = 0.1946 ）以及它们的梯度相似图。基于人类主观 DMOS，图像 “Fishing” 的质量比图像 “Flower” 高得多，然而二者的GMSM指标接近，而GMSD指标可以有明显差距，因此使用GMSD可以更有效的区分开一些质量分数不一样的数据。

三、实验

使用了以下几个数据集：LIVE（5 种失真）、CSIQ（6 种失真）、TID2008（17 种失真）。

消融实验：这里的消融实验不是针对GMSD来做的，而是其他方法，因为前面已经论述过平均池化没有优势。

这些方法原本的池化策略要么是平均池化，要么是加权池化。针对不同方法，SD（标准差） 池化的应用方式如下：

• 对于 MSE、SSIM、G-SSIM、GSD 和 FSIM，直接将 SD 池化应用于它们的局部质量图以生成预测质量分数。
• 对于 MS-SSIM，在每个尺度的局部质量图上应用 SD 池化，然后将所有尺度上的预测分数相乘作为最终分数。
  除 MSE 外，其他所有 IQA 方法在使用 SD 池化替代原始池化策略后，性能均未得到提升。原因可能在于：这些方法中，局部质量图是通过多种不同类型的特征生成的，特征之间的相互作用可能使图像局部质量的估计变得复杂，从而导致 SD 池化不适用。相比之下，MSE 仅使用原始亮度信息，GMSD 仅使用梯度幅度的亮度信息来计算局部质量图，这可能是 SD 池化对它们有效的原因。

定量实验，作者给出了多个方法的对比结果。

GMSD 在 CSIQ 和 TID2008 数据库上的 SRC（0.957、0.891）均排名第一，LIVE 数据库与 VIF、FSIM 相当。作者还绘制了一个排名图，这里更清晰的看出GMSD的效果优势。

对于特定失真类型实验：测试了每种类型失真的性能。

对于每个数据库和每个失真类型，前三个产生最高SROCC值的IQA指数以黑体高亮显示。GMSD表现非常均衡，除开某些特定的失真，例如CTC，这个失真在VSI中也有提到，是跟颜色相关的。

耗时：对IQA指标的运行速度进行了评价。

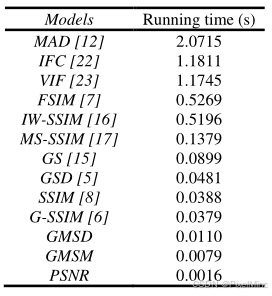
GMSD存在明显优势。

四、总结

本文提出了一种高效的全参考图像质量评估（FR-IQA）模型 ——梯度幅度相似性偏差（GMSD）。该模型通过计算参考图像与失真图像的像素级梯度幅度相似性（GMS） 生成局部质量图（LQM），并采用标准差池化策略（即 GMS 图的标准差）作为最终质量指标。实验表明，GMSD 在LIVE、CSIQ、TID2008三大数据库上的预测精度（如加权平均 SRC 达 0.924）优于多数现有模型，且计算效率极高（处理 512×512 图像仅需 0.0110 秒），兼具准确性与高效性，适用于实时图像质量评估场景。

代码部分将会单起一篇进行解读。（未完待续）

---

感谢阅读，欢迎留言或私信，一起探讨和交流，如果对你有帮助的话，也希望可以给博主点一个关注，谢谢。