[DFS] P1092 虫食算(提高+

Date：2019/10/19
Degree of difficulty：提高+
Original question：P1092 虫食算(提高+

Hi,又见面啦~


$$\to BeginHappily$$
首先看到这个题，还是被进制的外表吓到了，其实分析还是能得到一些东西的

1. 怎样输入
2. 搜索什么
3. 怎么剪枝

怎样输入

因为我对字符串这块还是不是很熟悉，所以这里需要强调一下

搜索什么

n 进制的加法就是在十进制的基础上满十进一改成满 n 进一
由于这道题只考虑加法，所以进位只可能是 1 ，证明小学生都会，略
搜索的大体思路就是从第 1 位的值开始搜，搜到最后一位，判断是否合法

怎样剪枝

原作：

作者: zzlzk 更新时间: 2017-08-22 15:37

1. 最高位不能有进位
2. 对于每一位，a数组加上b数组%n是等于c数组的（或a+b+1%n）

讲解

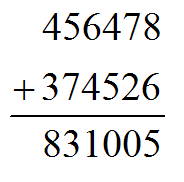
假设这是十进制下的加法，怎么判断这个竖式对不对？

显然这个竖式是错误的，因为个位上 $$(8+6)mod10=4\ne 5$$
由此推广到每一位，但是还要考虑进位，不慌，看另一张图

qwq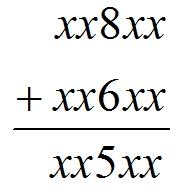

这个竖式是对的还是错的？
这并不好判断，虽然 $(8+6)mod10=4\ne 5$但是这是中间位，有可能有进位
如果有进位， 那么 $(8+6+1) mod 10=5 $，这一位就是合法的了。

玄学——Next数组

这里会用到一个next数组
要手动模拟一下

AC code

//Author:PhilFan;
#include<bits/stdc++.h>
#include<cstdlib>
#include<cstring>
using namespace std;
#define maxn 30
char 	s1[maxn],s2[maxn],s3[maxn];
int 	a[maxn],b[maxn],c[maxn];		//上面两行是用来存输入的字母的 
int 	next[maxn];						//玄学数组 
int 	n,cnt,num[maxn];				
bool 	used[maxn];						//存放用了的数 
//函数部分------------------------------------------------------------------ 
inline int change(char c){ 	//1.将字符转化为数字 
	return c-'A';
}
void print(){				//2.输出函数 
	for(int i = 0; i < n; i++){
		printf("%d ",num[i]);
	}
	exit(0);			//结束程序，在cstdlib库中 
} 
bool judge(){				//剪枝1 判断每一位是否都合法 
	for(int i = n-1,x=0; i >= 0;i--){
		int A = num[a[i]],B = num[b[i]],C = num[c[i]];
		if( ((A + B + x)%n) != C)	return false;
		x = (A+B+x)/n;
	} 
	return true;
}
bool prune(){				//剪枝2 判断当前位是否合法，%n和+1%n结果是不是此处得数 
	if(num[a[0]]+num[b[0]]>=n)	return true;
	for(int i = n-1; i >= 0; i--){
		int A = num[a[i]],B = num[b[i]],C = num[c[i]];
		if(A==-1||B==-1||C==-1)	continue;
		if( ((A + B + 1)%n) != C && ((A+B)%n)!=C ){
			return true;
		}
	}
	return false; 
}
void getnext(int x){		//3.生成用的
	if(!used[x]){
		used[x] = true;
		next[cnt++]=x;
	}
	return;
}
void dfs(int t){			//4. 搜索 产生1~n-1的全排列 
	if(prune()==true)	return;			//判断当前位，剪枝 
	if(t==n){
		if(judge()==true)	print();	//判断所有，输出 
		return;
	}
	for(int i = n-1; i >= 0; i--){		//递归循环部分 
		if(!used[i]){
			num[next[t]] = i;
			used[i] = 1;
			dfs(t+1);
			used[i] = 0;
			num[next[t]] = -1;
		}
	} 
	return;
}
//主函数部分------------------------------------------------------------------ 
int main()
{
	scanf("%d",&n);
	scanf("%s%s%s",s1,s2,s3);		//将输入的字母存到字符数组中去 
	for(int i = 0; i < n; i++){		//把字母变成数字 
		a[i]=change(s1[i]); 
		b[i]=change(s2[i]);
		c[i]=change(s3[i]);//把字符数组变成数字 
		num[i]=-1;//用于dfs里，是每个字母代表的值 
	}
	for(int i = n-1; i>=0;i--){		//Next 数组的应用，玄学东西，不是很懂 
		getnext(a[i]);
		getnext(b[i]);
		getnext(c[i]);
	}
	memset(used,0,sizeof(used));	//把getnext数组中的用过的used数组清零 
	dfs(0);							//开始搜索 
	return 0;
}

手动模拟过程

经过字母变数字和next玄学数组的处理后，我们的处理结果是这样的

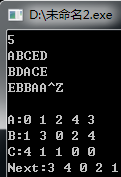
next是怎样出来的呢，

for(int i = n-1; i>=0;i--){		//Next 数组
		getnext(a[i]);
		getnext(b[i]);
		getnext(c[i]);
	}

这三行代码的过程是，我们来看

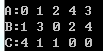
从右上角开始，把出现过的数字依次记录下来；

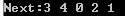
代表的字母分别是D E A C B

$$\to HappyEnding$$