[Exam]10.26 T104923 魔法部落

最新推荐文章于 2025-10-26 23:35:31 发布

原创最新推荐文章于 2025-10-26 23:35:31 发布 · 714 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#快速幂 #等比数列求和

基础算法同时被 2 个专栏收录

6 篇文章

订阅专栏

数学部分

1 篇文章

订阅专栏

本文深入解析了一道结合等比数列求和与快速幂算法的编程题，详细阐述了等比数列的基本公式及其在具体问题中的应用，并提供了完整的代码实现，适合初学者理解和掌握。

Date:2019/10/26

在这里插入图片描述
$→Perfect−Begining\to Perfect- Begining$
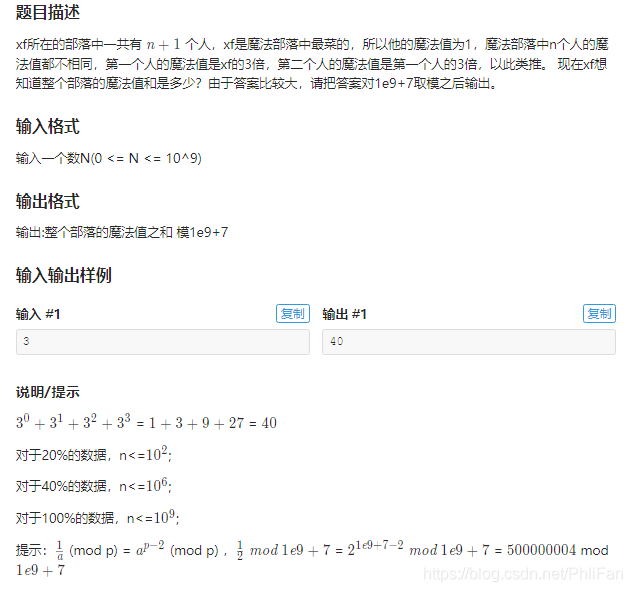
这道题是等比数列求和，再加上快速幂的板子；
其实挺简单的，就是当时做题的时候没有看懂最后一行

Math

先祭上等比数列求和的公式

定义式： $anan−1=q(n≥2,an−1≠0,q≠0\frac {a_n}{a_{n-1}} = q(n\geq 2, a_{n-1} \not = 0,q\not= 0$
通项公式： $an=a1×qn−1a_n = a_1\times q^{n-1}$
求和公式
$Sn=n∗a1(q≠1)S_n = n *a_1(q\not= 1)$
$Sn=a1(1−qn)1−qS_n= \frac {a_1(1-q^n)} { 1-q}$

而在这道题中， $a_1$ 是给定的，是1；
而 $q_n$ 也可以通过快速幂的板子来实现；

所以把已知条件带入求和公式，正好和题目给定的条件符合（~~我就说怎么原来不知道给定的是什么意思~~）

$1a(modp)=ap−2(modp)\frac {1}{a}(mod p) = a^{p-2}(mod p)$
$1e9+7)\frac {1}{2}(mod\:1e9+7) = a^{1e9+7-2}(mod\:1e9+7)$
$\;mod \; 1e9+7$

AC code

啥都不说了，我太菜了
水题都切不了，等比公式都不知道

//Author:PhilFan;
//等比数列求和公式+快速幂板子题 
#include<bits/stdc++.h>
using namespace std;
const long long mod = 1e9+7;
int n;
long long ans = 1,a;
void quick(){
	long long tmp = 3;
	while(n>0){
		if(n&1)	ans *= (ans*tmp) % mod;
		tmp = (tmp*tmp) % mod;
		n >>= 1;
	}
} 
int main()
{
	scanf("%d",&n);
	n+=1;
	quick();
	a = (500000004 % mod) * (ans-1) % mod;
	printf("%lld",a);
	return 0;
}

$Ending\to Perfect \:Ending$