【WebGPU学习杂记】数学基础拾遗（1）三角学基础

本文主要记录一些基础数学中的关键术语、公式、定义，方便查阅并基于此拓展和补充。部分内容需要有函数基础。
主要目的是熟悉这些公式即可，如果能够手推公式效果最理想（增加对公式的信任感）。

基础概念

• 内角、外角、补角、对边、临边
• 内角、外角和均为 $\pi$、任意两边长度加和 > 第三边
• 相似：
  • 三边对应成比例
  • 两边对应成比例且夹角相等
  • 两角对应角度相等
• 全等：三边相等、两边对应相等且夹角相等、双边角对应相等且夹边对应相等
• 单位圆、弧度制

几何直观

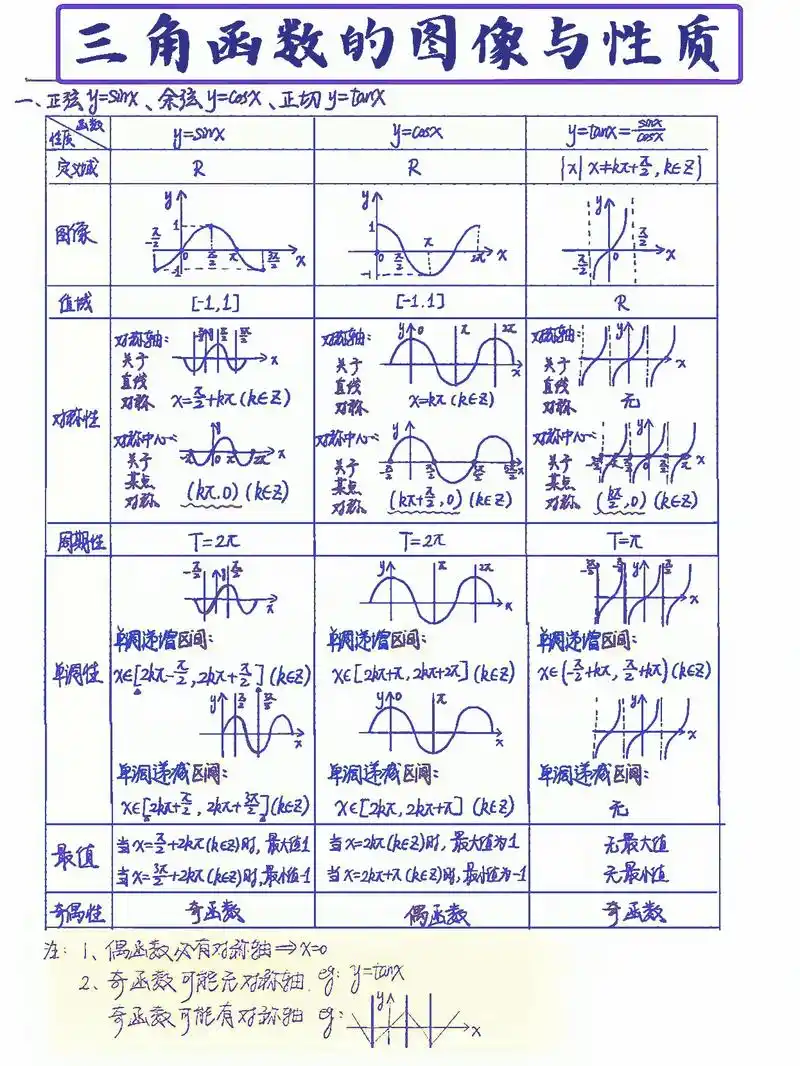
• 函数图像 $f(x)=\sin (x);f(x)=\cos (x);f(x)=\tan (x)$，了解奇偶特征、对称性、周期性、单调性、导数式
• 奇函数 $\sin (x)、\tan (x)$；偶函数 $\cos (x)$
• 对图像进行 平移、缩放、旋转、翻转 观察现象

基础公式

$${\sin }^{2}x+{\cos }^{2}x=1$$

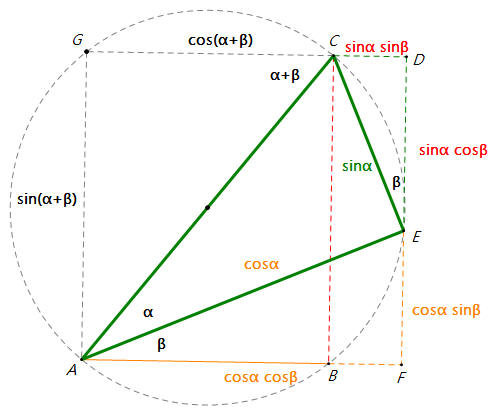
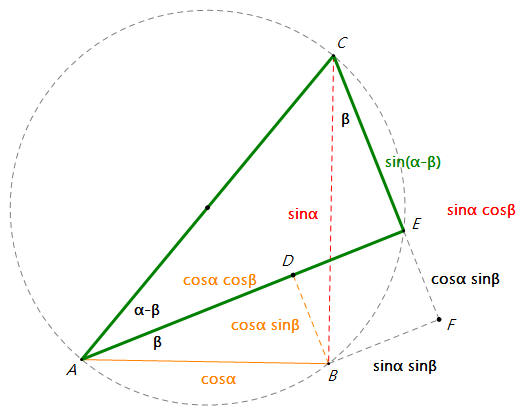
和差角公式（单位圆 + 向量点积、叉积定义方便推导）

sin⁡(α±β)=sin⁡αcos⁡β±cos⁡αsin⁡βcos⁡(α±β)=cos⁡αcos⁡β∓sin⁡αsin⁡βtan⁡(α±β)=tan⁡α±tan⁡β1∓tan⁡αtan⁡β \sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta \\ \cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta \\ \tan(\alpha \pm \beta) = \frac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta} sin(α±β)=sinαcosβ±cosαsinβcos(α±β)=<