Visual Object Tracking using Adaptive Correlation Filters(MOSSE)

Visual Object Tracking using Adaptive Correlation Filters[paper][code]

目标跟踪代码MOSSE出自2010年，此算法的最大贡献是使Frame Rate有了巨大的飞跃，论文中给出的Frame Rate为669fps，要知道达到realtime的条件是25fps，可见此算法速度之快。
摘要

• MOSSE对于光照、尺度、姿势和非刚性变化有很好的鲁棒性。
• MOSSE算法Frame Rate达到669fps，是当时最先进算法的20倍。
• 只从第一帧图像中提取特征
• 文中提到使用peak-to-sidelobe ratio(PSR)处理目标遮挡问题。
• MOSSE没有采样问题，其是使用当前帧目标的信息训练出一个过滤器，更新搜索区域使响应最大值位于搜索区域中心，然后在下一帧中，使用上一帧更新后的搜索区域在本帧截取相同位置，使用过滤器与截取区域执行相关操作，相关性最大的位置就是响应最大值位置，然后再更新过滤器，更新搜索区域。

预备知识

１．快速傅里叶变换(FFT):

• 快速傅里叶变换,将时域问题转为频域问题,得到数字信号的分析频谱.
• 傅里叶变换的基本思想是:任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加(带棱角的信号可以被无限接近).
• MATLAB中一维信号(如语音信号)用fft,二维信号(如图像信号)用fft2

2.需要注意两点

• 考虑图像的时候要用矩阵的思想去考虑图像,而不是单纯的图像形式.如mosse_amou版本代码有rand_warp函数中通过旋转图像从而提高模型鲁棒性,虽然在旋转过程时中心是不变,但是周围数值发生改变,而截取框大小位置不变,这时就会将背景截取进来。
• 进行高斯变换时，文中使用的是二维高斯变换 f(x,y)=A exp(-($\frac{(x-x_0{)}^2}{2{\sigma }_x^2}$+$\frac{(y-y_0{)}^2}{2{\sigma }_y^2}$)),其中A为幅值，($x_0$,$y_0$)为中心点坐标，${\sigma }_x$、${\sigma }_y$分别为x与y方差。
  在实际应用中，对于${\sigma }_x$、${\sigma }_y$我们取值一样,这样对于二维高斯模型在平面上投影就是一个圆形,意思是在与目标中心($x_0$,$y_0$)距离一样的点所获得的权重是一样的.若取不一样的值,那么投影为一个椭圆形,距离目标中心一样的点就会得到不一样的权重.

3.其他知识

• 傅里叶变换-解释的非常详细
• 频谱泄露-主要看频谱泄露问题，提到了采样频率问题(采样定理又称香农采样定理，奈奎斯特采样定理)
• 奈奎斯特采样定理-解释了采样频率问题和混叠问题
• 混叠-关于混叠的更详细解释
• 互相关与卷积问题-介绍了互相关和卷积数学上的不同
• 循环卷积-循环卷积与线性卷积和互相关都不同，这里先做简单了解
• 高斯函数分析-很详细
• 标准正态分布-由高斯函数我想到了标准正态分布，所以复习一下
• MATLAB窗函数-为什么加窗，MATLAB窗种类
• 汉宁窗-为什么加窗，介绍最常用的hann(汉宁窗)

MOSSE Filters理论

在傅里叶域内使用FFT计算图片相关性。
　　　　　　　　　　　　　　　　　　　　　　　　
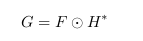
其中：Ｇ为目标跟踪区域图像，Ｆ为输入图像，${Ｈ}^{\ast }$为过滤器的共轭。
(这里滤波器使用共轭函数${Ｈ}^{\ast }$原因：在时域中ｇ = f⋆h,虽然文中一直说此为卷积操作，但是使用数学上的严格定义来说这里是互相关操作，但是在机器学习领域通常笼统的将互相关称为卷积，这种说法在Andrew Ng的深度学习课程中特地讲到过。)
则过滤器${Ｈ}^{\ast }$为：
　　　　　　　　　　　　　　　　　　　　　　　　　
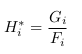
为了找到将训练输入映射到所需训练输出的滤波器，MOSSE找到一个滤波器H，它使实际卷积输出与期望卷积输出的平方误差之和最小。即：
　　　　　　　　　　　　　　　　　　　　　　　　　
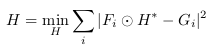
因为在傅里叶域内所有操作是相关元素乘法，所以滤波器H的每个元素都可以独立优化。因此优化问题可以从多变量优化问题转换为独立优化H的每个元素问题。
上式为凸函数，所以其只有一个最优解。因此在元素域内对H求偏导，使偏导为0的H即为最优解。
　　　　　　　　　　　　　　　　　　　　　　　　
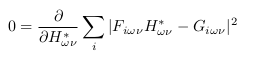
则：
　　　　　　　　　　　　　　　　
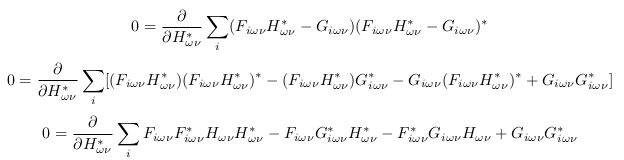
得：
　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　
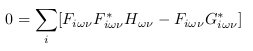
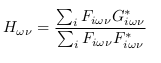
使用原始符号重写表达式：
　　　　　　　　　　　　　　　　　　　　　　　　
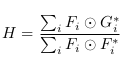
运算时要将分母加入小的噪音进行了正则化，适当的正则化可以使滤波器产生好的波形，同时避免了分母为零，也提高了系统鲁棒性：
　　　　　　　　　　　　　　　　　　　　　　　　
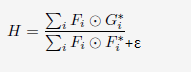
将上式求平均值，可以使滤波器快速跟踪对象，提高跟踪器速度：
　　　　　　　　　　　　　　　　　　　　　　　　

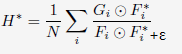
MOSSE Filters实际使用：Filter Initialization and Online Updates

上面我们完成了MOSSE滤波器在理论上的建模，在实际代码实现中我们定义MOSSE滤波器为：
　　　　　　　　　　　　　　　　　　　　　　　　
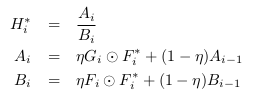
其中$\eta$为学习率。加入$\eta$可以使模型更加重视最近的帧，并使先前的帧的效果随时间呈指数衰减。文中给出的实验过程中得出的最优$\eta$=0.125，可以使滤波器快速适应目标外观的变化，同时仍保持好的稳健性。

Preprocessing

论文中提到,FFT卷积算法的一个问题是图像和滤波器被映射到环面的拓扑结构,人为的连接图像的边界引入影响相关输出的伪像,也就是造成了频谱泄露。为了解决上述问题,进行数据预处理：

• 使用对数函数变换图像像素值，有助于低对比度情况。
• 将像素值归一化为平均值为0，方差为1。
• 将图像进行加窗(文中直接提到加余弦窗)处理，从而可以将边缘像素值减小至0，有效防止频谱泄露。

注意的是:

• 要进行加窗操作一般在时域中进行,因为在时域中是点乘操作,在频域中是卷积操作.因此加窗操作是在傅里叶变换之前。
• 奇怪的是在 mosse_amou版本代码加窗后跟踪效果反而更差通过输出加窗前后特征图对比可以看到,加窗操作造成了许多特征信息丢失.
  解释:其实并不是加窗后跟踪效果变差,加窗操作就是突出裁剪图的中心位置,减弱边缘位置,因此加窗后跟踪器就将关注点放在了裁剪图的中心,而不是整个裁剪图,但是当我们裁剪整个物体时就会发现,跟踪器只跟踪物体中心位置,这就造成了误以为跟踪效果差的原因

MOSSE整体模型设计思路

1.基于第一帧中的对象为中心的跟踪窗口选择目标，获得目标在第一帧位置数据。
2.对第一帧截取目标区域进行二维高斯变换，得到目标输出$g_{desired}$,进行FFT得期望卷积输出$G_{desired}$。
3.preprocessing
4.更新过滤器参数，更新过滤器H。
5.读取第二帧图像，以第一帧目标位置信息截取输入图像，进行preprocessing处理。
6.将经过preprocessing处理过的第二帧截取图像f进行FFT得到F，将第二帧(第n帧)得到的F与第一帧(第n-1帧)得到的过滤器H点乘，得实际卷积输出$G_{actual}$,进行傅里叶反变换得实际输出$g_{actual}$
7.$g_{actual}$中最大值位置即为第二帧图像目标所在位置
8.以第二帧目标所在位置为中心重新对第二帧图像进行截图，然后进行preprocessing处理，得更新位置后第二帧截取图像F。
9.更新过滤器参数，更新过滤器H。
10.重复步骤5-9，直至程序结束。

Discussion

有许多简单的方法可以改进跟踪器：

• 如果目标相对稳定，则可以通过基于第一帧随机重定位来减轻漂移。
• 通过将更新之后的过滤跟踪窗口进行对数极坐标变换，可以使跟踪器应对目标尺度变化和旋转的问题。

Problem

通过运行各个数据集发现一个问题，当运行原代码时，会输出相关性大的位置作为响应最大值输出，但注意一点是，相关性大有时候会漂移不是目标中心点。
由于并未对新一帧图像做任何处理，当背景连续两帧出现在跟踪区域内，那在相关性上来说，这两帧在背景区域的相关性值也会很高，如果这个值超过目标中心点的值，那么就会造成漂移，这样就会造成以背景为主了，慢慢的会丢失目标。还有一种情况是如果背景中出现与目标上像素值一样的(如RedTeam数据集车上面有白色，而经过白色电线杆时就会误认为电线杆为目标)，认为电线杆正好也是白色，当与跟踪器相乘时，其相关性值也会很大，就会被误认为目标，这似乎是目标跟踪中另一个问题，就是目标与背景颜色相近的研究。
但是对图像加上高斯处理后，产生的新问题是，目标产生形变或旋转时，由于会造成目标中心移动，因此跟踪效果会不好。