齿轮模数：齿形设计的核心参数详解

模数的本质与重要性

模数(m)是齿轮设计中最基础的尺寸参数，它决定了齿轮齿形的绝对大小。模数可定义为：

m = 分度圆直径(d) / 齿数(z)

模数之所以是基础参数，是因为它：

• 直接决定了齿轮的齿距（p = π × m）
• 决定了齿轮的齿高（h = 2.25 × m）
• 影响齿轮的强度和承载能力
• 确保啮合齿轮的尺寸兼容性

模数对齿形的影响

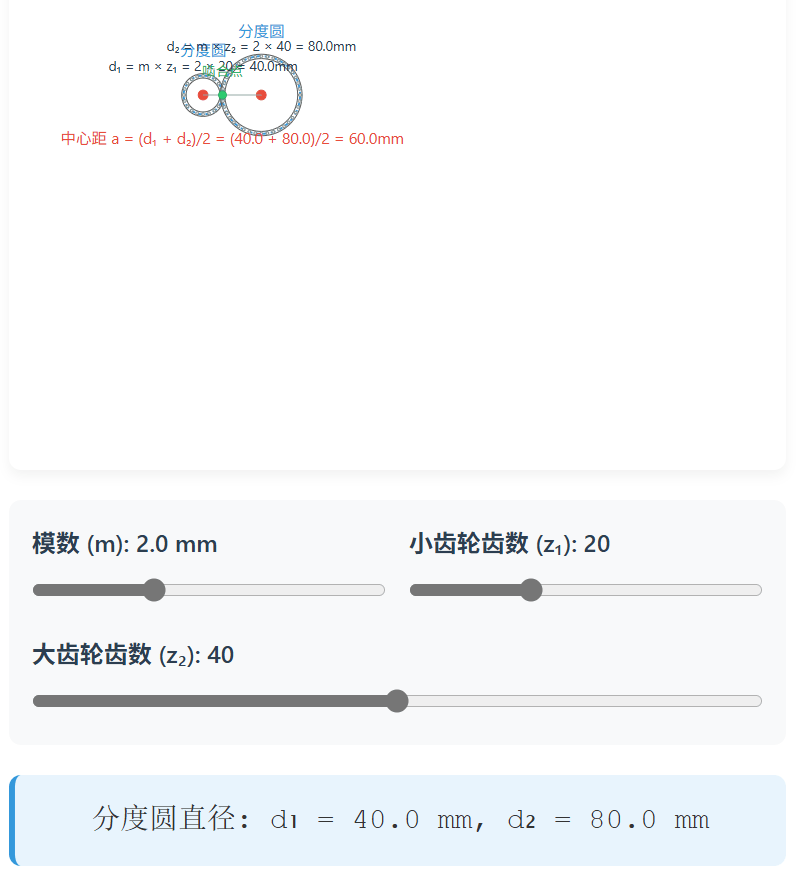
模数与关键齿轮参数的关系

1. 模数与齿距§

齿距是相邻两齿在分度圆上的弧长距离：

p = π × m

模数增大 → 齿距增大 → 齿槽变宽 → 可传递更大扭矩

2. 模数与齿高(h)

标准全齿高由模数决定：

全齿高(h) = 2.25 × m
齿顶高(ha) = 1 × m
齿根高(hf) = 1.25 × m

模数增大 → 齿高增大 → 接触面积增大 → 承载能力增强

3. 模数与分度圆直径(d)

分度圆是齿轮设计的基准圆：

d = m × z

相同齿数下 → 模数增大 → 分度圆直径增大 → 齿轮整体尺寸增大

4. 模数与强度

弯曲强度：

σ_b ∝ 1/m

模数增大 → 齿根厚度增加 → 抗弯强度提高

接触强度：

σ_h ∝ 1/√m

模数增大 → 接触面积增大 → 接触应力降低

模数选择工程实例

案例：输送机减速电机齿轮设计

要求：

• 输入功率：5.5kW
• 输入转速：1440rpm
• 输出转速：120rpm
• 工作寿命：20,000小时

设计步骤：

1. 计算总传动比：

   i = 1440/120 = 12
   

2. 初选模数（按经验公式）：

   m ≈ 10 × ∛(T/kz₁²)
   T = 9550 × P/n = 9550 × 5.5/1440 ≈ 36.5 N·m
   取k=10，z₁=20 → m ≈ 10 × ∛(36.5/(10×400)) ≈ 2.1
   

   选择标准模数 m=2.5mm

3. 齿数分配：

   第一级：i₁=4 → z₁=20, z₂=80
   第二级：i₂=3 → z₃=25, z₄=75
   

4. 齿轮尺寸计算：

   参数	第一级小齿轮	第一级大齿轮	第二级小齿轮	第二级大齿轮
   齿数(z)	20	80	25	75
   分度圆直径(d)	50mm	200mm	62.5mm	187.5mm
   齿顶圆直径(da)	55mm	205mm	67.5mm	192.5mm
   齿根圆直径(df)	43.75mm	193.75mm	56.25mm	181.25mm

5. 强度校核：

   • 弯曲强度校核：最大应力发生在第二级小齿轮

     σ_F = (2KT₁Y_F)/(b·m·d₁) ≤ [σ_F]
     

   • 接触强度校核：最大应力发生在第一级啮合点

     σ_H = Z_H·Z_E·√[(2KT₁)/(b·d₁²)·(u+1)/u] ≤ [σ_H]
     

模数选择设计准则

1. 优先选用标准模数系列：

   第一系列：1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10...
   第二系列：1.75, 2.25, 2.75, 3.5, 4.5, 5.5, 7, 9...
   

2. 考虑因素优先级：

   强度要求 > 空间限制 > 传动平稳性 > 制造成本
   

3. 不同应用场景推荐：

   应用场景	推荐模数范围	选择理由
   精密仪器	0.3-1.0mm	小尺寸，高精度
   通用机械	1.0-4.0mm	平衡强度与尺寸
   重型机械	4.0-10mm	高承载能力
   风电齿轮箱	10-30mm	超高扭矩传递需求

4. 避免常见错误：

   • 小模数齿轮用于重载场合导致断齿
   • 大模数齿轮用于高速场合引起振动噪声
   • 配对齿轮模数不一致导致啮合失败

结论

模数是齿轮设计的基石参数，它通过数学关系决定了齿轮的所有关键尺寸。合理选择模数需要：

1. 计算基本传动需求（功率、转速、扭矩）
2. 进行初步强度估算
3. 考虑安装空间限制
4. 选择最接近的标准模数值
5. 完成详细强度校核

掌握模数与其他参数的关联关系，是设计高效、可靠齿轮系统的关键第一步。实际设计中应借助专业软件（如Kisssoft、Romax）进行精确计算和优化。

公众号 | FunIO
微信搜一搜 “funio”，发现更多精彩内容。
个人博客 | blog.boringhex.top