本文详细介绍了驻定相位原理，用于求解复杂高频信号的近似积分，以线性调频（LFM）信号为例，通过推导和仿真验证，展示了LFM信号频域近似解的计算过程，揭示了B·τ与频谱差异的关系。
此文章讲解了驻定相位原理，并以线性调频信号为例，求解了LFM信号的频域近似解
引用请注明出处：https://blog.youkuaiyun.com/Panda123_/article/details/104513627
1 驻定相位原理的作用
是一种求解复杂高频扰动信号的近似积分方法。
2 原理简述
在驻相点附近，信号的相位变化非常小，对积分的贡献能够得以显现；而其他位置，相位变化非常大，积分近似等于零。
3 一般式推导
以通用信号(高频扰动信号) x ( t ) = A ( t ) e j θ ( t ) x(t)=A(t)e^{j\theta(t)} x(t)=A(t)ejθ(t)的傅里叶变换为例，推导驻定相位原理。
3.1 根据傅里叶变换定义
X
(
ω
)
=
∫
−
∞
+
∞
A
(
t
)
e
j
θ
(
t
)
e
−
j
ω
t
d
t
X(\omega)=\int_{-\infty}^{+\infty} A(t) e^{j \theta (t)}e^{-j \omega t}dt
X(ω)=∫−∞+∞A(t)ejθ(t)e−jωtdt
=
∫
−
∞
+
∞
A
(
t
)
e
j
[
θ
(
t
)
−
ω
t
]
d
t
=\int_{-\infty}^{+\infty} A(t)e^{j[\theta(t)-\omega t]}dt
=∫−∞+∞A(t)ej[θ(t)−ωt]dt
=
∫
−
∞
+
∞
A
(
t
)
e
j
ϕ
(
t
,
ω
)
d
t
= \int_{-\infty}^{+\infty} A(t)e^{j\phi(t,\omega)}dt
=∫−∞+∞A(t)ejϕ(t,ω)dt
其中，令
ϕ
(
t
,
ω
)
=
θ
(
t
)
−
ω
(
t
)
\phi(t,\omega) = \theta(t) - \omega(t)
ϕ(t,ω)=θ(t)−ω(t).
3.2 求驻定相位点 t 0 t_0 t0
令
ϕ
′
(
t
,
ω
)
∣
t
=
t
0
=
0
\phi^{' }(t,\omega)|_{t=t_0}=0
ϕ′(t,ω)∣t=t0=0
所得的
t
0
t_0
t0即为驻相点。
3.3 积分解析解
上述傅里叶变换的积分解析解为
X
(
ω
)
≈
−
π
2
ϕ
′
′
(
t
0
,
ω
)
⋅
e
−
j
π
/
4
⋅
A
(
t
0
)
⋅
e
j
ϕ
(
t
0
,
ω
)
X(\omega)\approx \sqrt{\frac{-\pi}{2\phi^{''}(t_0,\omega)}} \cdot e^{-j\pi/4} \cdot A(t_0) \cdot e^{j \phi (t_0,\omega)}
X(ω)≈2ϕ′′(t0,ω)−π⋅e−jπ/4⋅A(t0)⋅ejϕ(t0,ω)
该结果与二阶泰勒展开近似式一致。
4 线性调频信号频域表达式近似解
4.1 LFM信号时域表示式
x
(
t
)
=
r
e
c
t
(
−
τ
/
2
,
τ
/
2
)
⋅
e
j
π
k
t
2
x(t)=rect(- \tau/2,\tau/2 )\cdot e^{j \pi k t^2}
x(t)=rect(−τ/2,τ/2)⋅ejπkt2
其中，
k
k
k为调频斜率
k
=
B
τ
k=\frac {B}{\tau}
k=τB
B
B
B为信号带宽，
τ
\tau
τ为脉冲宽度。
4.2 推导结果
套用3.3节中解析解表达式，可得LFM信号频谱表达式为
X
(
f
)
=
j
1
4
k
⋅
e
−
j
π
/
4
⋅
e
j
π
f
2
k
X(f)=j \sqrt {\frac{1}{4k}} \cdot e^{-j \pi/4} \cdot e^{j \pi \frac{f^2}{k}}
X(f)=j4k1⋅e−jπ/4⋅ejπkf2
5 仿真验证
下面通过Matlab仿真，观察比较一下用该方法所得频域表达式和直接对时域信号
x
(
t
)
x(t)
x(t)作傅里叶变换所得频谱的差异。
仿真代码：link
5.1 B = 10 M H z , τ = 10 u s B=10MHz, \tau=10us B=10MHz,τ=10us
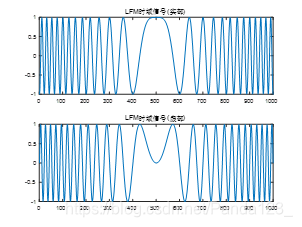
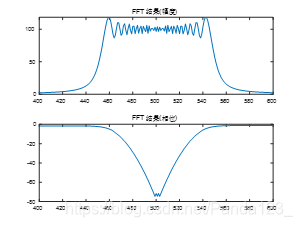
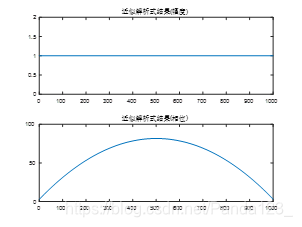
5.2 B = 50 M H z , τ = 10 u s B=50MHz, \tau=10us B=50MHz,τ=10us
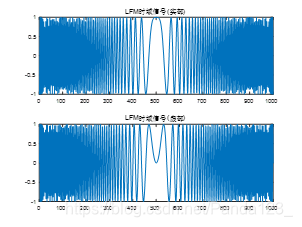
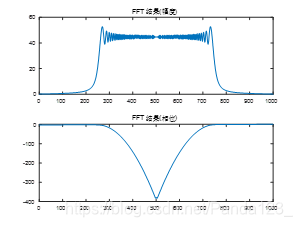
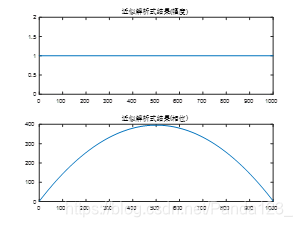
5.3 结论
可见，该差异与脉宽带宽积的大小有关， B ⋅ τ B \cdot \tau B⋅τ越大，则此差异越小，4.2节中所得解析表达式越接近真实频谱。
6 参考文献
需要此文中相应LFM时域频域仿真及驻定相位法结果仿真的朋友请参考下文：
https://download.youkuaiyun.com/download/Panda123_/12193759
扫一扫
1万+
到【灌水乐园】发言
