LeetCode刷题Day4--爬楼梯

LeetCode70. 爬楼梯（简单）

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

算法思想

动态规划思想

第一次选了1，则求后面n-1阶的方法数，第一次选了2阶，则求后面n-2阶的方法数
构造递归函数f(n) = f(n-1)+f(n-2)

代码实现

int climbStairs(int n){
    if(n==1)
       return 1;  
    else if(n==2)
       return 2;
    else
       return climbStairs(n-1)+climbStairs(n-2);
}

改正

错误分析：超时了

对动态规划理解有误，动态规划是省去重复子问题
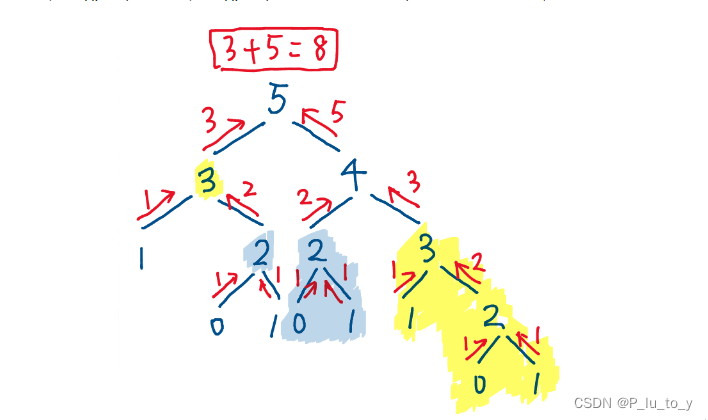如图，递归时，黄色阴影的3和蓝色阴影的2都是重复子问题；随着n增大，重复的子问题会更多，此时的时间复杂度为O(2^n),每个节点都遍历到。

正确解答

动态规划–自底向上的分析

要爬到第n阶要先n-1或者n-2阶楼梯，也就是dp[i] = dp[i-2] + dp[i-1]
相当于求n阶，只需要知道这三个数据，用一个数组，滚动得存放三个数据，即可降低到O(n)

代码实现

int climbStairs(int n){
    int  p=0, q=1, r=2;
    if(n==1) return 1;
    if(n==2) return 2;
    for(int i=3; i<=n; i++){
        p = q ;
        q = r ;
        r = p+q;
    }
    return r;
}