三种大数相乘算法

在研究Java的BigInteger乘法操作的源码时，在JDK的实现里看到了三种算法，调用multiply会根据两个乘数的大小进入不同的算法进行进一步的计算，他们分别是：

• 小学生算法（Grade-School Algorithm）
• Karatsuba算法（Karatsuba Algorithm | Brilliant Math & Science Wiki)
• Toom Cook-3算法

下面分别讲解各个算法，前面两种算法是比较好理解和实现的，而最后一种算法是比较复杂的。当然，本篇文章重点讲解三种算法的原理，实现部分参考JDK源码（BigInteger.java）即可。根据我的计划，之后的会有自己实现大数乘法的文章（也许会直接在此篇文章上增添）。

小学生算法

小学生算法，见名知意，就是小学数学课上学过的列竖式的方法，相比于下面两种算法，这个算法的思想和理论上的效果都显得很low。

那为什么JDK里还会采用这种算法而不是一股脑的用高级算法？这是因为下面这些甚至还有更高级的算法虽然在渐进意义上优势满满，但是时间复杂度前面的常数可不小，这样就导致在乘数比较小的时候，此算法还是具有优势的（比如JDK中，当两个乘数的二进制位数都大于$80\times 32$时才会采用下面的算法，否则的就直接利用小学生算法计算）。

算法思路

两个乘数$X$和$Y$，分别用$X$的每一位和$Y$的每一位相乘，将结果保存到对应的位置并且同时保留进位，每次相乘时将上次的进位加上同时也要将当前结果的对应位置的位加上。

令设$X,Y,Z$为三个整数，其中$Z$的位数等于$X$和$Y$的位数之和, 要求计算$X\times Y$并将结果存至$Z$中；

$X$，$Y$的位数分别为$4$，$2$；

设$N_i$表示整数$N$的第$i$位数，第$i$位是从低位到高位的从$0$开始计数的第$i$位；

算法过程如下图 :

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传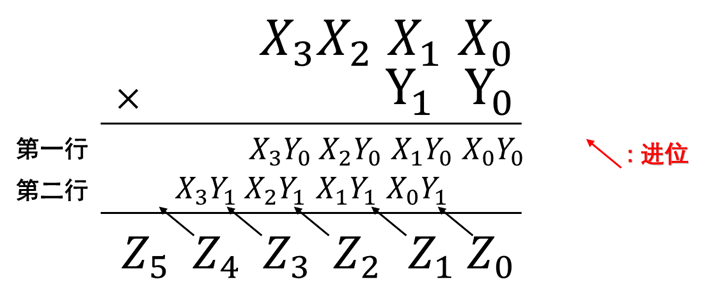

上图是通常的手算算法, 编程实现时, 还需要变换一下思路。手列竖式时，算完所有的行再算出$Z$的所有的位；编程时，每算一行时就算出此时的$Z$的对应的某一位，基本算法和手算相同（也需加上上一位的进位），不同的是还需加上$Z$的这一位之前的值。

JDK源码分析

@HotSpotIntrinsicCandidate // 该注解说明HotSpot内有本地的实现, 调用算法时会用本地实现替之
private static int[] implMultiplyToLen(int[] x, int xlen, int[] y, int ylen, int[] z) {
    int xstart = xlen - 1;
    int ystart = ylen - 1;

    if (z == null || z.length < (xlen + ylen))
        z = new int[xlen + ylen]; // 开辟z数组以存放结果

    long carry = 0;
    // 计算第一行
    // 第一行能算出Z的第0位到第xstart - 1位
    for (int j = ystart, k = ystart + 1 + xstart; j >= 0; j--, k--) {
        long product = (y[j] & LONG_MASK) *   // 相乘加上上次的进位
            (x[xstart] & LONG_MASK) + carry;
        z[k] = (int)product;
        carry = product >>> 32;
    }
    z[xstart] = (int)carry;

    for (int i = xstart - 1; i >= 0; i--) { // 计算其余行
        carry = 0;
        for (int j = ystart, k = ystart + 1 + i; j >= 0; j--, k--) {
            long product = (y[j] & LONG_MASK) *   // 相乘加上上次的进位, 同
                (x[i] & LONG_MASK) +              // 时还要加上该位之前的值
                (z[k] & LONG_MASK) + carry;
            z[k] = (int)product;
            carry = product >>> 32;
        }
        z[i] = (int)carry;
    }
    return z;
}

易得此算法的时间复杂度为平方级

Karatsuba算法

Karatsuba算法的思想是分而治之。

算法思路

该算法的思路是比较简单的，将两个乘数二分(设每一半位数为$h$)，

即令$X=X_h\cdot 2^h+X_l,Y=Y_h\cdot 2^h+Y_l$

则
$XY$
$=(X_h\cdot 2^h+X_l)(Y_h\cdot 2^h+Y_l)$
$=X_h{Y}_h\cdot 2^{2h}+X_h{Y}_l\cdot 2^h+X_l{Y}_h\cdot 2^h+X_l{Y}_l$

$=X_h{Y}_h\cdot 2^{2h}+(X_h{Y}_l+X_l{Y}_h)\cdot 2^h+X_l{Y}_l$

这样，效率就能高于小学生算法吗？

设算法的时间复杂度为$T(n)$，n代表乘数的位数
$$T(n)=\{\begin{array}{l}O(1),n\le n_0\\ 4T(n/2)+O(1),others\end{array}\text{\hspace{1em}(1)}$$
根据主定理，算得$T(n)=O(n^2)$，可见，算法效率并没有提高，

优化：

设$p1=X_h{Y}_h,p2=X_l{Y}_l,p3=(X_l+X_h)(Y_l+Y_h)=p1+p2+X_h{Y}_l+X_l{Y}_h$

易知$p3-p2-p1=X_h{Y}_l+X_l{Y}_h$正好是上面推得公式中$2^h$的系数。

所以：$XY=p1\cdot 2^{2h}+(p3-p1-p2)\cdot 2^h+p2$

利用这个公式进行计算，计算$XY$的所需的乘法次数减为了3次
$$T(n)=\{\begin{array}{l}O(1),n\le n_0\\ 3T(n/2)+O(1),others\end{array}\text{\hspace{1em}(1)}$$

根据主定理，算得$T(n)=O(n^{lo{g}_{2}3})=O(n^{1.585})$，可见，算法效率提高了一些，但是这产生了递归调用和加法的开销，这也是导致大数乘法不能无脑选择高级算法的原因。

JDK源码分析

private static BigInteger multiplyKaratsuba(BigInteger x, BigInteger y) {
    int xlen = x.mag.length;
    int ylen = y.mag.length;

    // The number of ints in each half of the number.
    int half = (Math.max(xlen, ylen)+1) / 2; // 二分

    // xl and yl are the lower halves of x and y respectively,
    // xh and yh are the upper halves.
    // 分别获取x, y的高低一半
    BigInteger xl = x.getLower(half);
    BigInteger xh = x.getUpper(half);
    BigInteger yl = y.getLower(half);
    BigInteger yh = y.getUpper(half);

    // 根据公式计算结果, 下面的multiply调用都可能再调用multiplyKaratsuba, 即递归
    
    BigInteger p1 = xh.multiply(yh);  // p1 = xh*yh
    BigInteger p2 = xl.multiply(yl);  // p2 = xl*yl

    // p3=(xh+xl)*(yh+yl)
    BigInteger p3 = xh.add(xl).multiply(yh.add(yl));

    // result = p1 * 2^(32*2*half) + (p3 - p1 - p2) * 2^(32*half) + p2
    //        = (p1 * 2^(32*half) + (p3 - p1 - p2)) * 2^(32*half) + p2
    //        = (p1 * 2^(32*half) +
    //           (p3 - p1 - p2)) *
    //           2^(32*half) +
    //           p2
    BigInteger result = p1.shiftLeft(32*half).
        				add(p3.subtract(p1).subtract(p2)).
                        shiftLeft(32*half).
        				add(p2);

    if (x.signum != y.signum) { // 异号还需要取个相反数
        return result.negate();
    } else {
        return result;
    }
}

**思考：**如果长度不够怎么分组？很简单，假设足够长就行（高位用0补），所以分组的大小取两个乘数中较大的那个的位数的一半，JDK里的getLower/getUpper的确是这么实现的，后面Toom Cook算法的分组也是这种思路。

Toom Cook-3算法

Toom Cook也是基于分而治之的算法，Toom Cook-k算法就是指将乘数分别分为固定大小的k组进行计算的算法。Toom Cook算法可以当做Karatsuba算法的泛化版本，会使用并不难，但是想要理解为什么要这么操作是有难度的。此文章仅对于Toom Cook-3算法进行具体操作层面的讲解。Toom Cook算法的介绍、起源、原理等内容将会单独出一篇文章进行详细讲解。

算法思路

同样设两个乘数$X$和$Y$

将它们分别等分为3份，即,
$$X=X_2\cdot t^2+X_1\cdot t+X_0$$

$$Y=Y_2\cdot t^2+Y_1\cdot t+Y_0$$
其中 t = 2 m a x { b i t N u m ( X ) , b i t N u m ( Y ) } / 3 t=2^{max\{bitNum(X),bitNum(Y)\}/3} t=2max{bitNum(X),bitNum(Y)}/3

那么，

$XY=(X_2\cdot t^2+X_1\cdot t+X_0)(Y_2\cdot t^2+Y_1\cdot t+Y_0)$

$$\begin{gathered} =X_0{Y}_0{t}^0+X_0{Y}_1{t}^1+X_0{Y}_2{t}^2+ \\ {X}_1{Y}_0{t}^1+X_1{Y}_1{t}^2+X_1{Y}_2{t}^3+ \\ {X}_2{Y}_0{t}^2+X_2{Y}_1{t}^3+X_2{Y}_2{t}^4 \end{gathered}$$

$$\begin{gathered} =X_0{Y}_0+ \\ (X_0{Y}_1+X_1{Y}_0)t+ \\ (X_0{Y}_2+X_1{Y}_1+X_2{Y}_0)t^2+ \\ (X_1{Y}_2+X_2{Y}_1)t^3+ \\ {X}_2{Y}_2{t}^4 \end{gathered}$$

$=w_0+w_{1}t+w_2{t}^2+w_3{t}^3+w_4{t}^4$

如果直接按照这个式子算，时间复杂度递推式：
$$T(n)=\{\begin{array}{l}O(1),n\le n_0\\ 9T(n/3)+O(1),others\end{array}\text{\hspace{1em}(1)}$$
根据主定理时间复杂度$T(n)=O(n^2)$没有优势，接下来就是老办法，用一系列骚操作将乘法次数减少，带来的代价是其他操作次数增多和算法更加麻烦（不用复杂这个词，防止歧义）。

之所以说是老办法，是因为这种办法挺常见的，Karatsuba算法、Strassen算法（矩阵乘法）都是这种思路，这些算法除了应用还有的意义是证明了有胜于普通解法的可能。由于这些算法复杂度的常数很大，要求输入达到某个规模以上才有优势，甚至可能只有理论意义而没有很大的实践意义，大数乘法最佳的算法甚至能达到无限接近常数，但是这些算法自带的缺点使得没有很大的实践意义。

好了，不扯了😂，上骚操作，不予证明、不予推导，这些将会单独在前文提到的另一篇文章中详细说明。

“易设”🤣$a,b,c,d,e$分别为：
$a=X_0{Y}_0$
$b=(X_0+X_1+X_2)(Y_0+Y_1+Y_2)$
$c=(X_0-X_1+X_2)(Y_0-Y_1+Y_2)$
$d=(X_0+2X_1+4X_2)(Y_0+2Y_1+4Y_2)$
$e=(X_0-2X_1+4X_2)(Y_0-2Y_1+4Y_2)$

“易知” 🤣：
$w_0=a$
$w_1=(8b-8c-d+e)/12$
$w_2=(-30a+16b+16c-d-e)/24$
$w_3=(-2b+2c+d-e)/24$
$w_4=(6a-4b-4c+d+e)/24$

乘积$XY=w_0+w_{1}t+w_2{t}^2+w_3{t}^3+w_4{t}^4$将$w_i$带入即可得出乘积结果。

这样计算，时间复杂度递推式：
$$T(n)=\{\begin{array}{l}O(1),n\le n_0\\ 5T(n/3)+O(1),others\end{array}\text{\hspace{1em}(1)}$$
根据主定理时间复杂度$T(n)=O(n^{lo{g}_{3}5})=O(n^{1.465})<O(n^2)$，理论上好于小学生算法和Karatsuba算法。

JDK源码分析

JDK的实现为了尽力的提高速度，用了一些数学上的等价变换（比如用移位代替乘除），所以可读性比较差，不过沉下心来读还是可以读懂的。

• 乘除尽量用移位实现
• 为了尽可能减少计算次数，可能利用了一些中间结果，比如假设需要$2a$和$4a$这两个数字，会先算出$2a$（利用移位）并用了它（$2a$），再用$2a$算出$4a$并也用了它（$4a$）
• $x/12、x/24$的操作被装换成了先除以3再利用移位，比如$x/12=(x/3)>>2$
• 多项式的计算被稍加转换，比如$a{x}^2+bx+c\to (ax+b)x+c$

private static BigInteger multiplyToomCook3(BigInteger a, BigInteger b) {
    int alen = a.mag.length;
    int blen = b.mag.length;

    int largest = Math.max(alen, blen); // largest/3即每组的大小

    // k is the size (in ints) of the lower-order slices.
    int k = (largest+2)/3;   // Equal to ceil(largest/3)

    // r is the size (in ints) of the highest-order slice.
    int r = largest - 2*k;

    // Obtain slices of the numbers. a2 and b2 are the most significant
    // bits of the numbers a and b, and a0 and b0 the least significant.
    BigInteger a0, a1, a2, b0, b1, b2;
    
    // 分组，a和b都被分为三组
    a2 = a.getToomSlice(k, r, 0, largest);
    a1 = a.getToomSlice(k, r, 1, largest);
    a0 = a.getToomSlice(k, r, 2, largest);
    b2 = b.getToomSlice(k, r, 0, largest);
    b1 = b.getToomSlice(k, r, 1, largest);
    b0 = b.getToomSlice(k, r, 2, largest);

    BigInteger v0, v1, v2, vm1, vinf, t1, t2, tm1, da1, db1;

    // 算系数
    
    v0 = a0.multiply(b0, true);
    da1 = a2.add(a0);
    db1 = b2.add(b0);
    vm1 = da1.subtract(a1).multiply(db1.subtract(b1), true);
    da1 = da1.add(a1);
    db1 = db1.add(b1);
    v1 = da1.multiply(db1, true);
    v2 = da1.add(a2).shiftLeft(1).subtract(a0).multiply(
        db1.add(b2).shiftLeft(1).subtract(b0), true);
    vinf = a2.multiply(b2, true);

    t2 = v2.subtract(vm1).exactDivideBy3(); // exactDivideBy3是专门除以三的操作, 为了快
    tm1 = v1.subtract(vm1).shiftRight(1);
    t1 = v1.subtract(v0);
    t2 = t2.subtract(t1).shiftRight(1);
    t1 = t1.subtract(tm1).subtract(vinf);
    t2 = t2.subtract(vinf.shiftLeft(1));
    tm1 = tm1.subtract(t2);

    // Number of bits to shift left.
    int ss = k * 32;

    // 算xy
    BigInteger result = 
        vinf.shiftLeft(ss).
        add(t2).shiftLeft(ss).
        add(t1).shiftLeft(ss).
        add(tm1).shiftLeft(ss).
        add(v0);

    if (a.signum != b.signum) { // 异号还需要取个相反数
        return result.negate();
    } else {
        return result;
    }
}

分析下来，应该可以理解什么小学生算法还有应用价值了。

小学生，yyds！(≥◇≤)

该文章首次被发布在我的个人博客上,
文章链接 三种大数相乘算法