算法补完计划(三) 最短路-优快云博客

本文介绍了基础图论算法Floyd-Warshall用于求最短路径，Dijkstra算法的模板及其限制，以及SPFA算法的扩展，探讨了如何在有向图中检测连通性和寻找最小环。重点讲解了负权边处理和单源最短路径的实现，并提到了SPFA在检测负环的应用。

比较基础的图论算法，直接放板子了。。

Floyd

可爱的 $O(n^{3})$ 算法

代码

for(int k = 1;k <= n;k ++)
		for(int i = 1;i <= n;i ++)
			for(int j = 1;j <= n;j ++)
				dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);

求最短路

n<=500可以一试

判断图的连通性（有向 and 无向皆可）

稍微一改，dis[i][j] == 1说明联通，反正说明不连通

若u，v之间存在一条有向边，则dis[u][v] = 1

for(int k = 1;k <= n;k ++)
		for(int i = 1;i <= n;i ++)
			for(int j = 1;j <= n;j ++)
				dis[i][j] = dis[i][j] || (dis[i][k] && dis[k][j]);

找最小环

首先求最短路时dis[i][j]其实是已经减过一维的了（第一维对结果无影响），对于dis[k][i][j]，表示(i d到 j的路径中，所有结点都小于等于 k 的最短路径长度）

正在学。。。改天再补

来补力

for(int k = 1;k <=n; k++){
    for(int i = 1;i <= k-1; i++)
        for(int j = i+1; j <= k-1; j++)
            ans = min(ans, dis[i][j] + val[i][k] + val[k][j]);
    for(int i = 1;i <= n; i++)
        for(int j = 1; j <= n; j++)
            dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}

我们val[i][j]记录 i 到 j 的边权，遍历到k时说明 k - 1及之前的点都处理完了，来个图

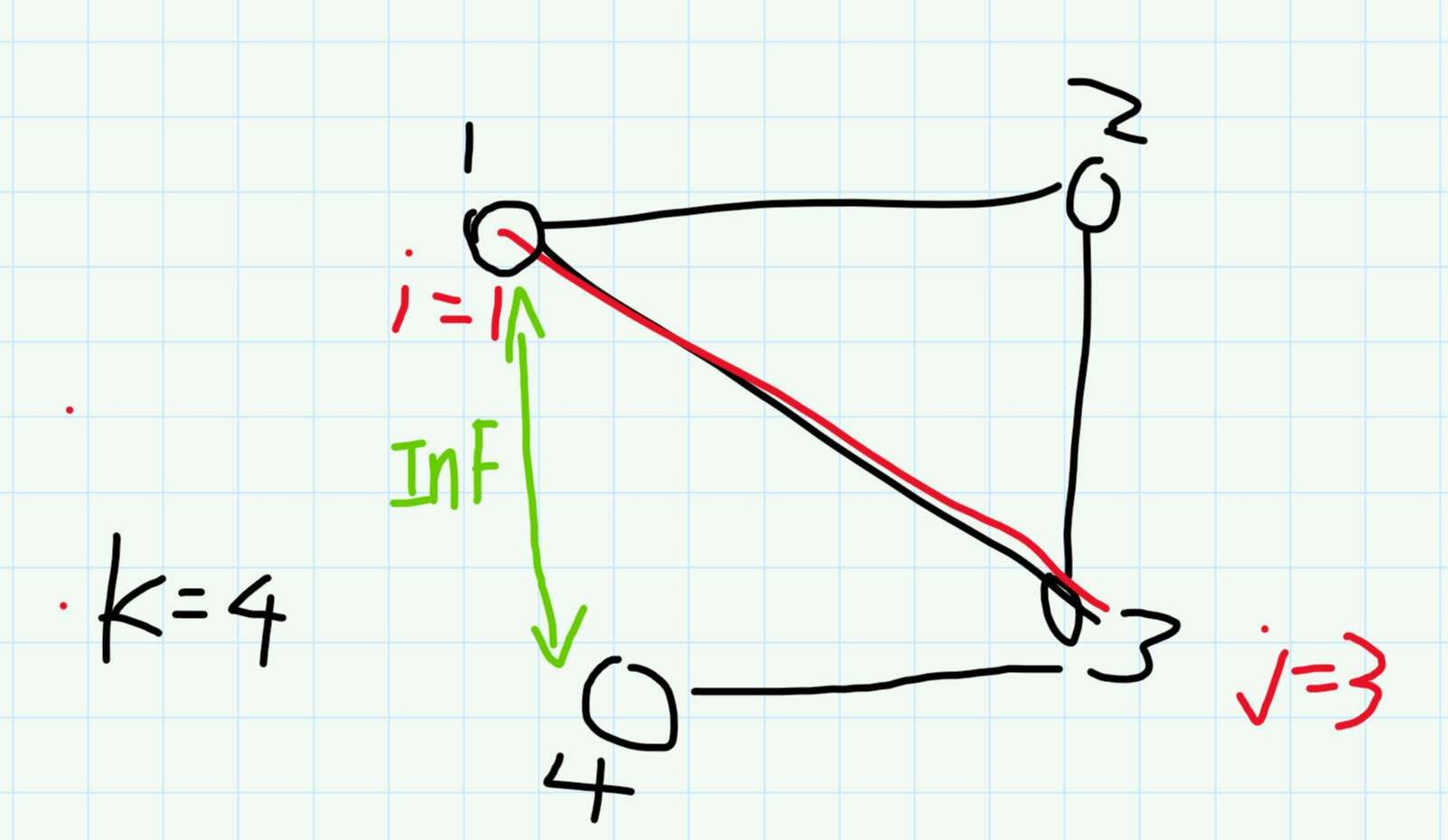
k = 4时，dis[][]（i = 1 ... 3，j = 1 ...3 ）已经处理好，其实这里的4就相当于新加进来的点，然后判断能不能与之前的点构成环，然后进行更新，使用带权并查集的话我们基本就是这个思路。

在floyd中，边权的初始值是INF，我们这里可以不判断直接更新，因为构不成环的话更新也不会改变ans，更新的话就是ans = min ( ans ，dis[i][j] + val[i][k] + val[k][j] ）

在上图，k = 3 时会产生dis[1][2] + val[1][3] + val[3][2] 的成功更新，而k = 4 时则不会

add：在网上找到的好像都是无向图，不知道存在单向边的图能不能用。。希望找个题练练

Dijkstra

典

P4779 【模板】单源最短路径（标准版）

	#include<bits/stdc++.h>
	using namespace std;
	struct Node{
		int u, v, val, next;
	}edge[210000];
	struct node{
		int u, dis;
	};
	struct cmp{
		bool operator ()(node a, node b){
			return a.dis > b.dis;
		}
	};
	int n, m, s, cnt;
	int head[110000], vis[110000], dis[110000];
	void add(int u, int v, int val){
		edge[++cnt].u = u;
		edge[cnt].v = v;
		edge[cnt].val = val;
		edge[cnt].next = head[u];
		head[u] = cnt;
	}
	void dij(int x){
		priority_queue < node, vector<node>, cmp> q;
		dis[x] = 0;
		q.push((node){x, 0});
		while(!q.empty()){	
			node now = q.top();
			q.pop();
			int u = now.u;
			if(vis[u]) continue;
			vis[u] = 1;
			for(int i = head[u];i;i = edge[i].next){
				int v = edge[i].v;
				if(dis[v] > dis[u] + edge[i].val){
					dis[v] = dis[u] + edge[i].val;
					q.push((node){v, dis[v]});
				}
			}
		}
	}
	int main(){
		cin >> n >> m >> s;
		//for(int i = 1;i <= n;i ++)dis[i] = 1e9;
		memset(dis, 0x7f, sizeof(dis));
		for(int i = 1;i <= m;i ++){
			int u, v, val;
			cin >> u >> v >> val;
			add(u ,v, val);
		}
		dij(s);
		for(int i = 1;i <= n;i ++)
			cout << dis[i] <<" ";
			
		return 0;
	}

需要注意的是，dij不能处理存在负权边的图

SPFA

典+1，就是说dij的板子改改就成spfa了。。。

P3371 【模板】单源最短路径（弱化版）

#include<bits/stdc++.h>
using namespace std;
struct node{
	int u, v, val, next;
}edge[510000];
int n, m, s, cnt;
int head[110000], in[110000];
long long dis[110000];
void add(int u, int v, int val){
	edge[++cnt].u = u;
	edge[cnt].v = v;
	edge[cnt].val = val;
	edge[cnt].next = head[u];
	head[u] = cnt;
}
void spfa(int x){
	queue<int> q;
	q.push(x);
	dis[x] = 0;
	in[x] = 1;//in[]数组表示当前元素是否在队列中
	while(!q.empty()){	
		int u = q.front();
		q.pop();
		in[u] = 0;
		for(int i = head[u];i;i = edge[i].next){
			int v = edge[i].v;
			if(dis[v] > dis[u] + edge[i].val){
				dis[v] = dis[u] + edge[i].val;
				if(!in[v]){
					q.push(v);
					in[v] = 1;
				}			
			}
		}
	}
}
int main(){
	cin >> n >> m >> s;
	for(int i = 1;i <= n;i ++)dis[i] = 1e18;
	//memset(dis, 0x7f, sizeof(dis));
	for(int i = 1;i <= m;i ++){
		int u, v, val;
		cin >> u >> v >> val;
		add(u ,v, val);
	}
	spfa(s);
	for(int i = 1;i <= n;i ++)
	if(dis[i] != 1e18)
		cout << dis[i] <<" ";
	else cout << "2147483647"<<" ";
	return 0;
}