数据结构补完计划(一) 线段树

原创已于 2022-07-06 23:00:47 修改 · 1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #数据结构 #图论

于 2022-04-11 16:25:31 首次发布

算法专栏收录该内容

15 篇文章

订阅专栏

本文详细讲解了如何使用线段树数据结构进行区间加法、乘法操作，并介绍了lazy标记和mul标记的应用，包括递归构建、pushdown操作和区间查询的更新过程。通过实例展示了在给定[1,8]区间内对[3,7]区间元素进行修改的操作步骤。

P3372 【模板】线段树 1

建树：

void build(int o, int l, int r){
    t[o].l = l;t[o].r = r;
    if(l == r){
        t[o].val = a[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(l, mid, o<<1);
    build(mid+1, r, o<<1|1);
    t[o].val = t[o<<1].val + t[o<<1|1].val;
}

区间加：

void add(int o, int l, int r, int w){
    if(l <= t[o].l&&t[o].r <= r){//当前区间被包含
        t[o].add += w;
        t[o].val += (t[o].r - t[o].l + 1) * w;
        return ;
    }
    pushdown(o);
    int mid = (t[o].l + t[o].r) >> 1;
    if(l <= mid) add(o<<1, l, r, w);
	if(mid+1 <= r) add(o<<1|1, l, r, w);
	t[o].val = t[o<<1].val + t[o<<1|1].val;
}

画个图，假设[1,8]区间，让[3,7]区间每个元素加2，最后会递归到以下结点。

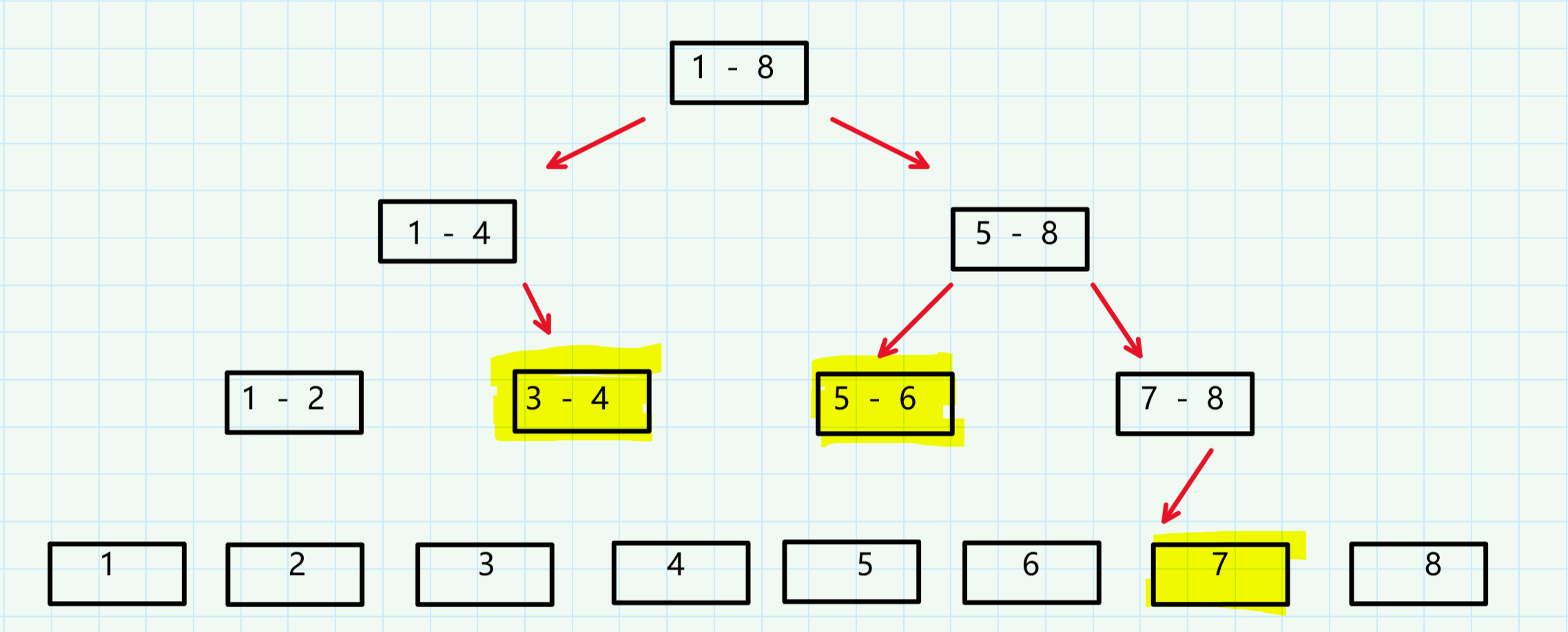
对于满足 l <= t[o].l && t[o].r <= r 即当前结点的范围被操作区间[3, 7]覆盖时，就无需继续递归下去。令当前结点的懒标记为 2 ，sum += 所含点数 * 2。

若不满足则继续往左右两个子树递归，注意需要先pushdown()，即把懒标记下放。

懒标记(lazytag)：给符合范围的结点进行标记，表示这段区间所加过的值，从而不用递归到最底层。

当我们进行查询或者区间加值的时候，在递归下去时需要下放懒标记。

：能看出来的是，lazy标记是表示该节点的儿子累计加的值，该结点本身的sum已经加上了。

void pushdown(int o){
	t[o<<1].val += t[o].add * (t[o<<1].r - t[o<<1].l + 1);
	t[o<<1|1].val += t[o].add * (t[o<<1|1].r - t[o<<1|1].l + 1);
	t[o<<1].add += t[o].add;
    t[o<<1|1].add += t[o].add;
    t[o].add = 0;
	return ;
}

区间和查询：

ll ask(int o, int l, int r){
    if(t[o].l >= l && t[o].r <= r){
        return t[o].val ;
    }
    pushdown(o);
    ll sum = 0;
    int mid = (t[o].l + t[o].r) >> 1;
    if(l <= mid) sum += ask(o<<1, l, r) ;
    if(mid+1 <= r) sum += ask(o<<1|1, l, r) ;
    return sum%mod;
}

和区间加差不多

区间乘法：

现在增加一个操作，令[l,r]区间里的数 * k ，引入乘法操作后，加一个新标记 mul 记录乘法操作。

先把 mul 和 sum 乘上 k

对于之前已经有的 add ，把它乘上 k 即可。

void mul(int o, int l, int r, int k) { //区间乘法
	if (l <= t[o].l && t[o].r <= r) {
		t[o].add = (t[o].add%mod * k%mod) % mod;
		t[o].mul = (t[o].mul%mod * k%mod) % mod;
		t[o].val = (t[o].val%mod * k%mod) % mod;
		return;
	}
	pushdown(o);
	int mid = (t[o].l + t[o].r) >> 1;
	if (l <= mid) mul(o << 1, l, r, k);
	if (r >= mid+1) mul(o << 1|1, l, r, k);
    t[o].val = (t[o<<1].val%mod + t[o<<1|1].val%mod ) % mod;
	return;
}

下面的问题是pushdown操作，我们给父节点的mul 和 add都乘上了k，按照先乘后加的顺序，因为乘法会对之前的加法产生影响，所以分别乘完之后再加。

比方说区间的val先加2再乘3，父节点的sum每次加，乘完已经算好了，假设这里的子结点的值为5，正常顺序是(5 + 2) * 3，我们让add = 2 * 3 = 6，mul = 3，所以下传时 5 * mul + add = 5*3 + 2*3 = （5 + 2）* 3。（其实就是结合率。。。

简单的细节处理后，pushdown的代码如下

引入mul后的pushdown操作：

void pushdown(int o){
    t[o<<1].val = (t[o<<1].val%mod * t[o].mul%mod) % mod +  (t[o].add%mod * (t[o<<1].r - t[o<<1].l + 1)%mod)%mod;
    t[o<<1|1].val = (t[o<<1|1].val%mod * t[o].mul%mod) % mod +  (t[o].add%mod * (t[o<<1|1].r - t[o<<1|1].l + 1)%mod)%mod;
    t[o<<1].mul = (t[o<<1].mul%mod * t[o].mul%mod) % mod;
    t[o<<1|1].mul = (t[o<<1|1].mul%mod * t[o].mul%mod) % mod;
	t[o<<1].add = (t[o<<1].add%mod * t[o].mul%mod + t[o].add%mod) % mod;
    t[o<<1|1].add = (t[o<<1|1].add%mod * t[o].mul%mod + t[o].add%mod) % mod;
    t[o].mul = 1;
    t[o].add = 0;
	return ;
}

大板子：

P3373 【模板】线段树 2

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n, m, mod;
int a[400000];
struct node{
    int l, r;
    ll val, mul, add;
}t[400000];
void pushdown(int o){
    t[o<<1].val = (t[o<<1].val%mod * t[o].mul%mod) % mod +  (t[o].add%mod * (t[o<<1].r - t[o<<1].l + 1)%mod)%mod;
    t[o<<1|1].val = (t[o<<1|1].val%mod * t[o].mul%mod) % mod +  (t[o].add%mod * (t[o<<1|1].r - t[o<<1|1].l + 1)%mod)%mod;
    t[o<<1].mul = (t[o<<1].mul%mod * t[o].mul%mod) % mod;
    t[o<<1|1].mul = (t[o<<1|1].mul%mod * t[o].mul%mod) % mod;
	t[o<<1].add = (t[o<<1].add%mod * t[o].mul%mod + t[o].add%mod) % mod;
    t[o<<1|1].add = (t[o<<1|1].add%mod * t[o].mul%mod + t[o].add%mod) % mod;
    t[o].mul = 1;
    t[o].add = 0;
	return ;
}
void add(int o, int l, int r, int w){
    if(l <= t[o].l&&t[o].r <= r){//当前区间被包含
        t[o].add += w;
        t[o].val += (t[o].r - t[o].l + 1) * w % mod;
        return ;
    }
    pushdown(o);
    int mid = (t[o].l + t[o].r) >> 1;
    if(l <= mid) add(o<<1, l, r, w);
	if(mid+1 <= r) add(o<<1|1, l, r, w);
	t[o].val = (t[o<<1].val%mod + t[o<<1|1].val%mod) % mod;
}
void mul(int o, int l, int r, int k) { //区间乘法
	if (l <= t[o].l && t[o].r <= r) {
		t[o].add = (t[o].add%mod * k%mod) % mod;
		t[o].mul = (t[o].mul%mod * k%mod) % mod;
		t[o].val = (t[o].val%mod * k%mod) % mod;
		return;
	}
	pushdown(o);
	int mid = (t[o].l + t[o].r) >> 1;
	if (l <= mid) mul(o << 1, l, r, k);
	if (r >= mid+1) mul(o << 1|1, l, r, k);
    t[o].val = (t[o<<1].val%mod + t[o<<1|1].val%mod ) % mod;
	return;
}
ll ask(int o, int l, int r){
    if(t[o].l >= l && t[o].r <= r){
        return t[o].val % mod;
    }
    pushdown(o);
    ll sum = 0;
    int mid = (t[o].l + t[o].r) >> 1;
    if(l <= mid) sum += ask(o<<1, l, r) % mod;
    if(mid+1 <= r) sum += ask(o<<1|1, l, r) % mod;
    return sum%mod;
}
void build(int o, int l, int r){
    t[o].l = l;t[o].r = r;t[o].mul = 1;
    if(l == r){
        t[o].val = a[l] % mod;
        return ;
    }
    int mid = (l + r) >> 1;
    build(o<<1, l, mid);
    build(o<<1|1, mid+1, r);
    t[o].val = (t[o<<1].val%mod + t[o<<1|1].val%mod) % mod;
}
int main(){
    cin >> n >> m >> mod;
    for(int i = 1;i <= n;i ++)
        scanf("%d",&a[i]);
    build(1, 1, n);
    while(m --){
        int num;
        scanf("%d",&num);
        if(num == 1){
            int x, y, k;
            scanf("%d %d %d",&x,&y,&k);
            mul(1, x, y, k);
        }
        if(num == 2){
            int x, y, k;
            scanf("%d %d %d",&x,&y,&k);
            add(1, x, y, k);
        }
        if(num == 3){
            int x, y;
            scanf("%d %d",&x,&y);
            cout << ask(1, x, y)%mod << endl;
        }
    }
    return 0;
}