数据结构补完计划(二) 权值线段树

基本原理

权值线段树基于普通线段树，不同点是，权值线段树某区间内的数的出现次数。

比如一段序列1，1，2，2，2，3，4， 那么结点值如下

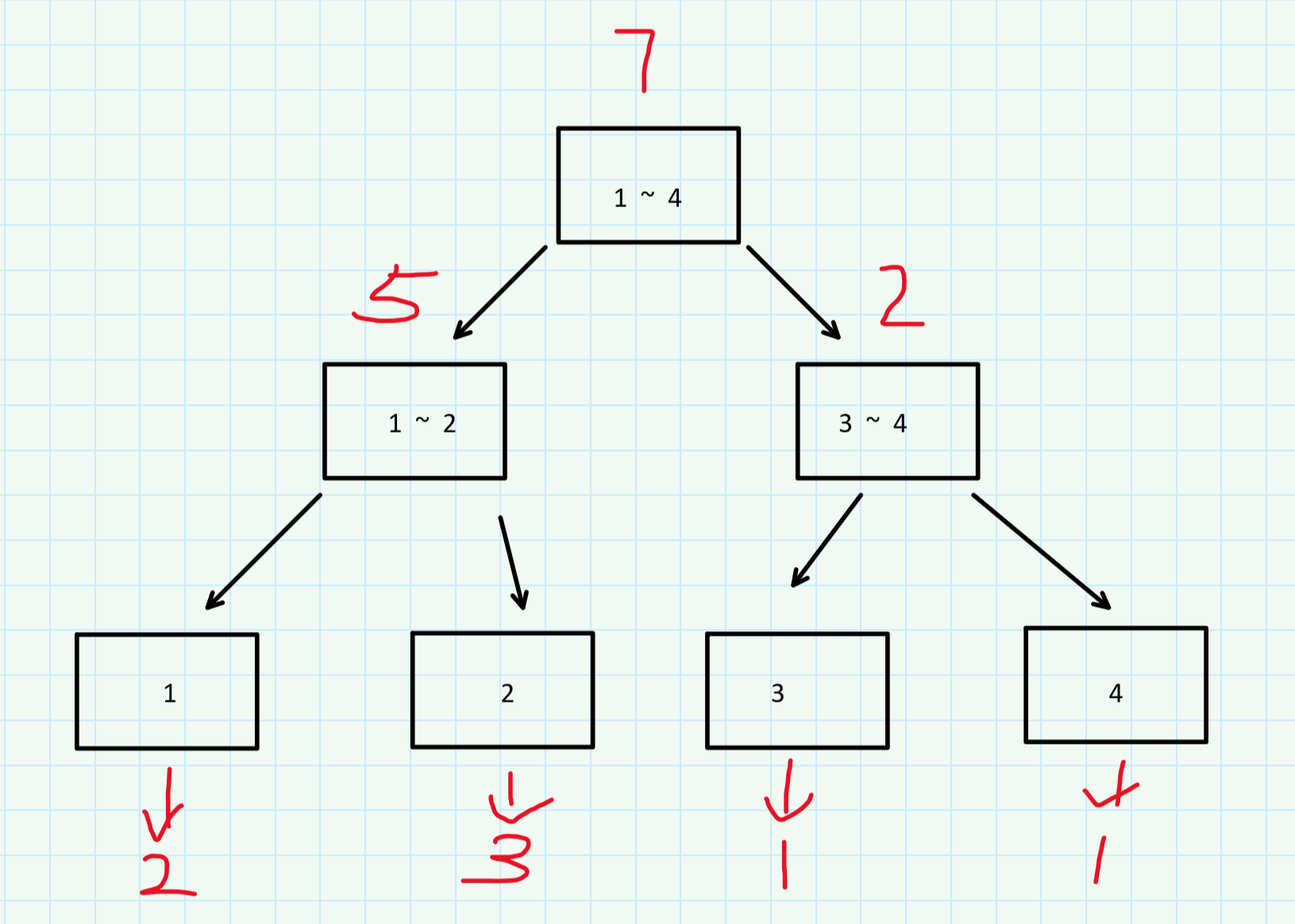
基本原理就这样（很好理解。。

需要注意的是，因为数据的范围会很大，需要动态开点以及离散化

基本操作

离散化

可以用STL库中的unique函数

void init(){
    int r = -1;
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
        b[i] = a[i];
    } 
    sort(b + 1, b + n + 1);
    int m = unique(b + 1, b + n + 1) - b - 1;//去重,unique返回的是尾地址+1
    for(int i = 1; i <= n; i++){
        a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
        r = max(r, a[i]);
    }
}

添加新元素

void add(int o,int l, int r, int x){
	if(l == r){
        t[o]++; 
        return;
    } 
    int mid = (l + r) >> 1;
	if(x <= mid) add(o << 1, l, mid, x);
    else add(o << 1 | 1, mid + 1, r, x);
    t[o] = t[o << 1] + t[o << 1 | 1];
}

查询某数出现的次数

void find(int o, int l, int r, int x){
	if(l == r) return t[o]; 
    int mid = (l + r) >> 1;
	if(x <= mid) return find(o << 1, l, mid, x);
    else return find(o << 1 | 1, mid + 1, r, x);
}

查询一段区间内的数出现的次数

int find(int l, int r, int o, int x, int y){//x,y为查询区间
    if (l == x && r == y) return t[o];
    int mid = (l + r) >> 1;
    if (y <= mid) return find(l, mid, o << 1, x, y);
    else if (x > mid) return find(mid + 1, r, o << 1 | 1, x, y);
    else return find(l, mid, o << 1, x, mid) + find(mid + 1, r, o << 1 | 1, mid + 1, y);//这里要把查询区间分开
}

*查询第K大/小的元素

假如找第K小的数，从结点开始，若K > 左子树值，说明在右子树中，这时在右子树寻找第（k - 左子树值）的数（因为已经包含了左子树

int query(int o, int l, int r, int k){//求区间第k小的数
	if(l == r) return l;
	int mid = (l + r) >> 1;
	if(k > t[o << 1]) return query(o << 1 | 1, mid + 1, r, k - t[o << 1]);
    else return query(o << 1, l, mid, k);
}

int query(int o, int l, int r, int k){//第k大
    if(l == r) return l;
    int mid = (l + r) >> 1;
    if(k > t[o << 1 | 1]) return query(o << 1, l, mid, k - t[o << 1 | 1]);
    else return query(o << 1, mid + 1, r, k);
}

---

P1637 三元上升子序列

 权值线段树正反动态加点两次，记录small[i]，big[i]，即第i个数之前有几个比它小，有几个比他大，统计答案ans += small[i] * big[i]

#include<bits/stdc++.h>
using namespace std;
int n,t[600000],a[600000],b[600000], r=-1 ;
int small[600000], big[600000];
long long ans;
void init(){
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
        b[i] = a[i];
    } 
    sort(b + 1, b + n + 1);
    int m = unique(b + 1, b + n + 1) - b - 1;//去重,unique返回的是尾地址+1
    for(int i = 1; i <= n; i++){
        a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
        r = max(a[i], r);
    }
}
void add(int o, int l, int r, int x){
	if(l == r){
        t[o]++; 
        return;
    } 
    int mid = (l + r) >> 1;
	if(x <= mid) add(o << 1, l, mid, x);
    else add(o << 1 | 1, mid + 1, r, x);
    t[o] = t[o << 1] + t[o << 1 | 1];
}
int find(int l, int r, int o, int x, int y){
    if (l == x && r == y) return t[o];
    int mid = (l + r) >> 1;
    if (y <= mid) return find(l, mid, o << 1, x, y);
    else if (x > mid) return find(mid + 1, r, o << 1 | 1, x, y);
    else return find(l, mid, o << 1, x, mid) + find(mid + 1, r, o << 1 | 1, mid + 1, y);
}

int main(){
    init();
    for(int i = 1;i <= n;i++){
        if(a[i] > 1) small[i] +=find(1, r, 1, 1, a[i]-1);
        //cout << small[i] << " ";
        add(1, 1, r, a[i]);
    }
    memset(t, 0, sizeof(t));
    for(int i = n;i >= 1;i--){
        if(a[i] < r) big[i] += find(1, r, 1, a[i]+1, r);
        //cout << big[i] << " ";
        add(1, 1, r, a[i]);
    }
    for(int i = 1;i <= n;i ++)
        ans += small[i] * big[i];
    cout << ans;
	return 0;
}