4 张 GIF 图帮助你理解二叉查找树

（给程序员的那些事加星标）

二叉查找树（Binary Search Tree），也称二叉搜索树，是指一棵空树或者具有下列性质的二叉树：

• 任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

• 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

• 任意节点的左、右子树也分别为二叉查找树；

• 没有键值相等的节点。

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等。（摘自维基百科）

下面 4 张 GIF 动图，是 penjee 官博制作分享，正好伯小乐最近看到，分享给大家。

图1：查找 BST 中的某个元素

在二叉搜索树b中查找x的过程为：

1. 若b是空树，则搜索失败，否则：

2. 若x等于b的根节点的数据域之值，则查找成功；否则：

3. 若x小于b的根节点的数据域之值，则搜索左子树；否则：

4. 查找右子树。

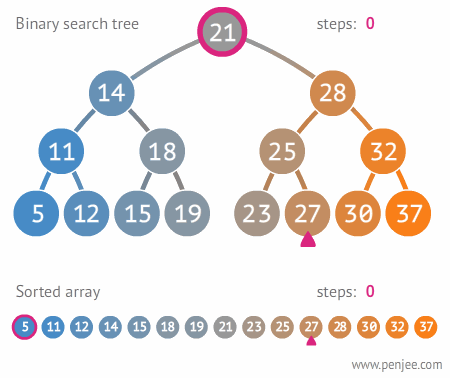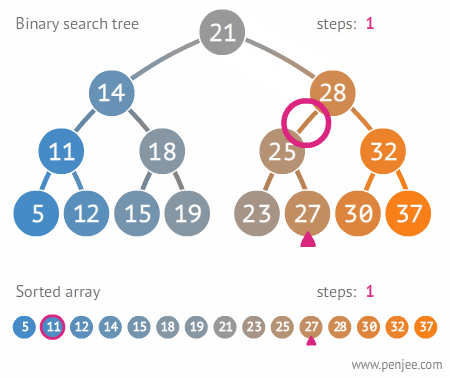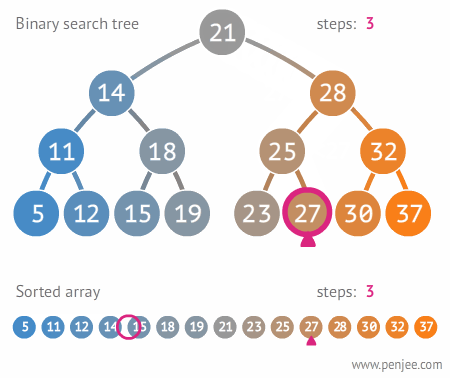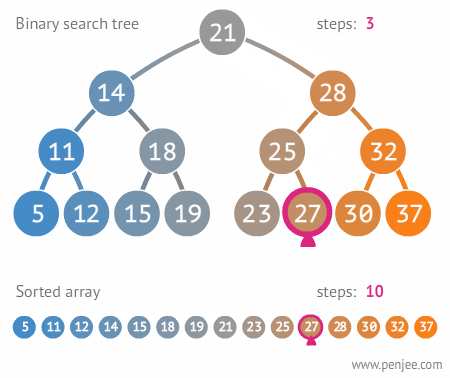
图2 ↓ ：从有序数组构造一个二叉查找树

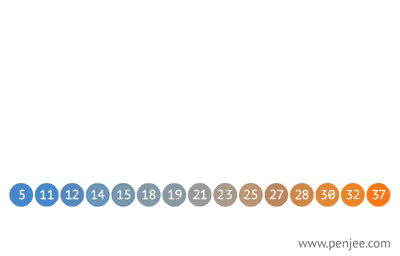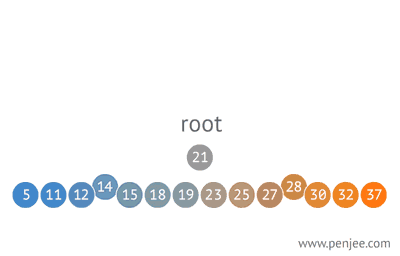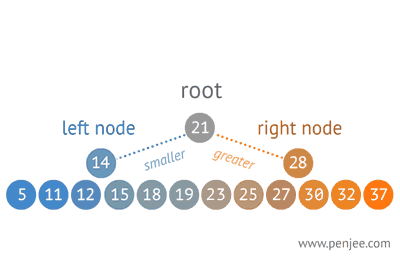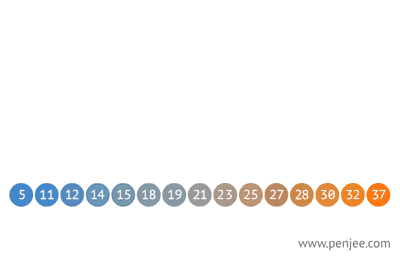
图3 ↓：往 BST 中插入元素

向一个二叉搜索树b中插入一个节点s的算法，过程为：

1. 若b是空树，则将s所指结点作为根节点插入，否则：

2. 若s->data等于b的根节点的数据域之值，则返回，否则：

3. 若s->data小于b的根节点的数据域之值，则把s所指节点插入到左子树中，否则：

4. 把s所指节点插入到右子树中。（新插入节点总是叶子节点）

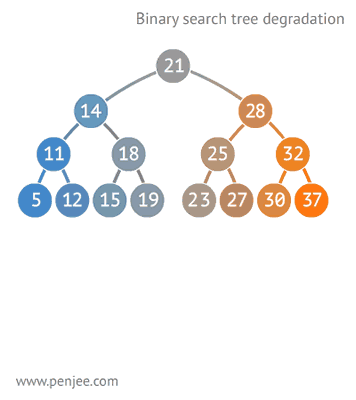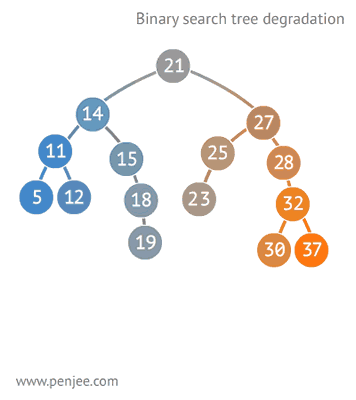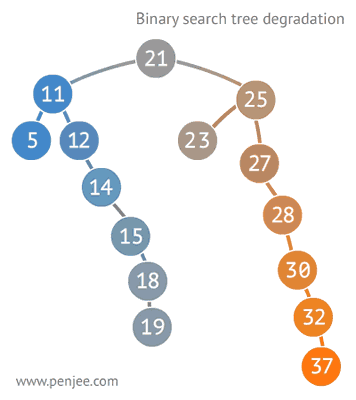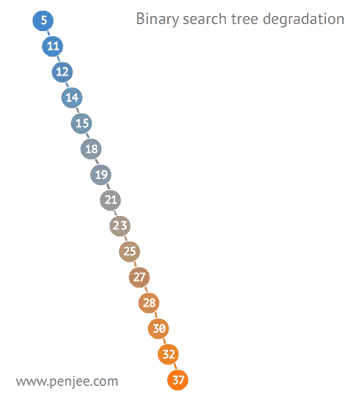
图4 ↓：BST 转成有序数组

往期热文（点击图片即可阅读）

关注「程序员的那些事」加星标，不错过圈内事

好文章，我在看❤️