主成分分析系列（一）概览及为什么数据要中心化

一、概览

主成分分析（Principle Component Analysis，PCA）算法属于数据降维算法里面的一种。数据降维算法的主要想法是从高维度数据中找到一种结构，这种结构蕴含了数据中的大部分信息，从而将高维数据降维到低维数据，方便观察、可视化与后续处理。准确地说，PCA算法是在较低维空间中寻求原始数据最准确的数据表示。

二、PCA算法在2维上的一个例子

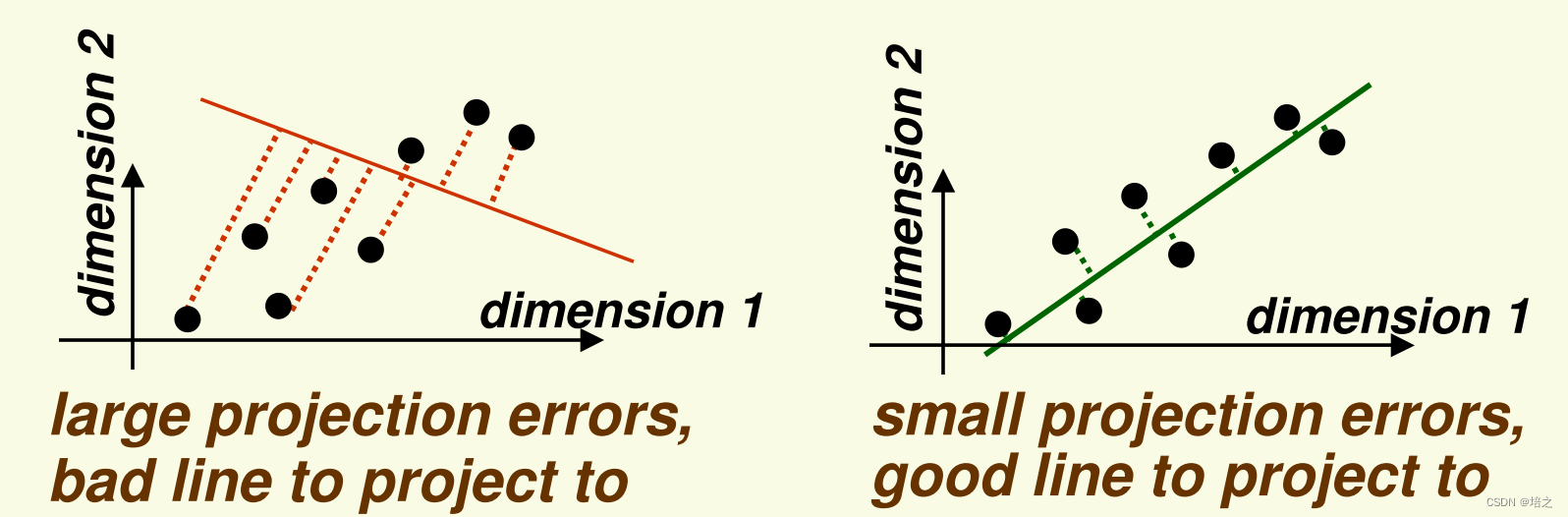
图一展示将数据 $\mathbf{x}$ 投影到一维子空间（一条直线，但其实这里说一维子空间有些不严谨，但是不影响理解，后文有说明），以最小化投影误差。投影误差是点到直线的距离（左图是红色虚线，右图是绿色虚线）。
请注意，从图一上观察到，用于投影的直线，右图中的比左图中的好，因为数据 $\mathbf{x}$ 在后者上投影误差更小。
直观上看，用于投影的最小化数据 $\mathbf{x}$投影误差的方向同时就是使得数据 $\mathbf{x}$方差最大的方向。这个在后面的文章会有数学推导证明。

图 1:

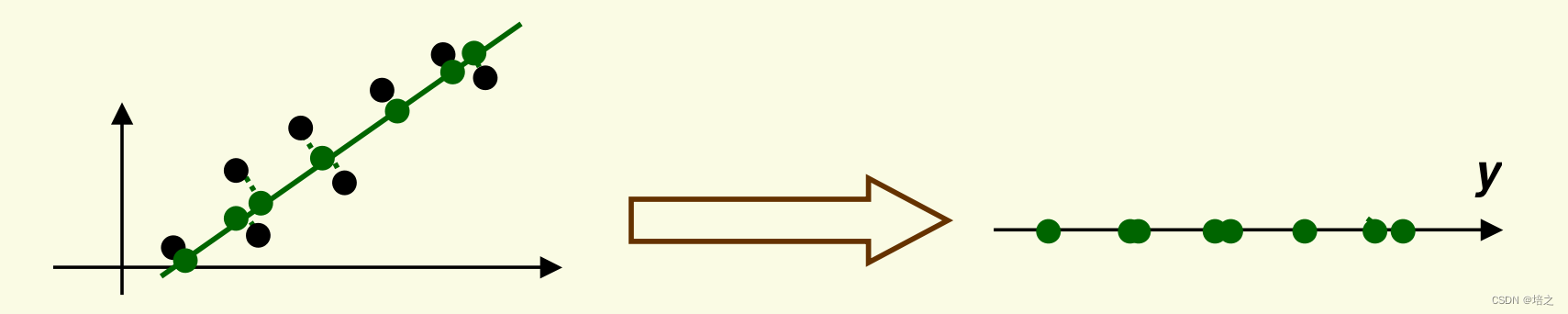
选取图一右侧的直线作为投影直线。数据投影到投影线上后的结果如图2右侧所示。

• 请注意，投影得到的新数据 $\mathbf{y}$ 与旧数据 $\mathbf{x}$ 在投影方向(绿色直线)方向上具有相同的方差。
• PCA 保留数据中最大的方差。 我们将证明这个结论，目前这只是 PCA 将做什么的直觉。

图 2:

为推导PCA算法需要的线性代数知识准备

设 $\mathbf{V}$ 为 $d$ 维 线性空间，$\mathbf{W}$ 为 $\mathbf{V}$ 的 $k$ 维线性子空间。
我们总能找到一组 $d$ 维向量 { e1,e2,…,ek}\{\mathbf {e_1,e_2,…,e_k}\}{ e1​,e2​,…,ek​}，它形成 $\mathbf{W}$的一组正交基 。