大模型技术在全球范围内持续演进,各大科技公司纷纷推出新一代模型,重点强化智能体方向的核心能力,包括编程、工具使用和深度信息检索等,无一不在提升实际问题解决能力。伴随着技术升级,越来越多能够解决实际问题的智能体正在涌现——它们能够自主规划任务、协同执行指令,在科研、编程、商业分析等领域展现出切实价值。与此同时,中国大模型在全球持续引人注目,在海外社区引发广泛讨论,展示出中国在大模型研发与应用方面的强劲实力。
司南持续关注大模型的发展动态,近期针对国内外主流大语言模型进行了全面评测,现公布司南最新(即10月)大语言模型评测榜单!本次榜单囊括了国内外共27个大语言模型,包含国内外主流闭源模型和社区开源模型。
最新榜单解读
-
GPT-5-2025-08-07保持领先优势
在本次榜单评测中,来自OpenAI、深度求索、字节豆包、通义千问、腾讯混元等多个厂商发布的模型在各个评测维度展开激烈的竞争。最终由OpenAI发布的GPT-5-2025-08-07以其在多个维度上表现出的强大能力,成功卫冕榜首,在上次榜单和本次榜单中的综合得分均位列第一。
-
国产模型能力进步显著,发展趋势向好
在本次榜单评测中,GLM-4.6、Qwen3-235B-A22B-Thinking-2507、iFlytek-Spark-X1preview-Think-1025、Doubao-Seed-1.6-251015 (Thinking)、DeepSeek-R1-0528等国内各大厂商发布的模型均凭借其过硬的综合能力跻身前列,与国外主流闭源模型不相上下;其他国产模型亦紧随其后,数学、推理、工具调用等多维能力相较过往进步显著。
-
全球科技企业竞逐工具调用能力,开闭源模型齐头并进
工具调用能力是衡量大模型智能体(Agent)能力的关键基石。从全球竞争格局来看,国内外头部科技企业、研究机构在该领域呈现出白热化的角逐态势。值得注意的是,这一技术赛道的竞争已突破传统"开源vs闭源"的二元框架——无论是以闭源模式保持技术闭环的商业巨头,还是依托开源社区实现快速迭代的创新力量,均在工具调用能力上展现出强劲的技术实力。最新榜单测试数据显示,部分顶尖开源模型在标准化工具调用任务中的成功率已与头部闭源模型持平,甚至在特定场景中展现出独特优势,这种"势均力敌"的格局正推动整个行业向更开放、多元的技术生态演进。
榜单更新说明
相较于2025年7月榜单,本次榜单的主要更新包括:
-
新增模型:Claude Sonnet 4.5 (Thinking)、Claude Haiku 4.5 (Thinking)、Doubao-Seed-1.6-251015 (Thinking)、Hunyuan-T1-20250822、iFlytek-Spark-X1preview-Think-1025、Nanbeige3.5-Pro-Thinking等闭源模型,以及gpt-oss-120b (high)、DeepSeek-V3.2-Exp、MiniMax-M2、Ring-1T-preview、GLM-4.6、Qwen3-Next-80B-A3B-Thinking等开源模型。
-
评测内容迭代:持续优化评测流程,确保评测稳定性,加强评测客观程度。针对代码评测集和推理评测集的内容做出调整,并根据社区对大模型不同能力维度的关注度变化,修正模型综合得分的计算公式。
月度榜单评测基准
司南大语言模型官方自建评测榜单,综合评估商业API模型和开源模型在 语言、推理、知识、代码、数学、工具调用六大能力维度,这些维度进一步细化为包括自然语言处理、理工科知识、学科推理、数学竞赛,多轮工具调用等十余项细分任务,以实现对行业开源模型和商业API模型进行全面评测分析。
*不同能力维度会根据任务形式选用主观或客观评测方案。总分基于各能力维度加权获得: 语言(1/9)、推理(2/9)、知识(1/9)、代码(1/9)、数学(2/9)、工具调用(2/9)。
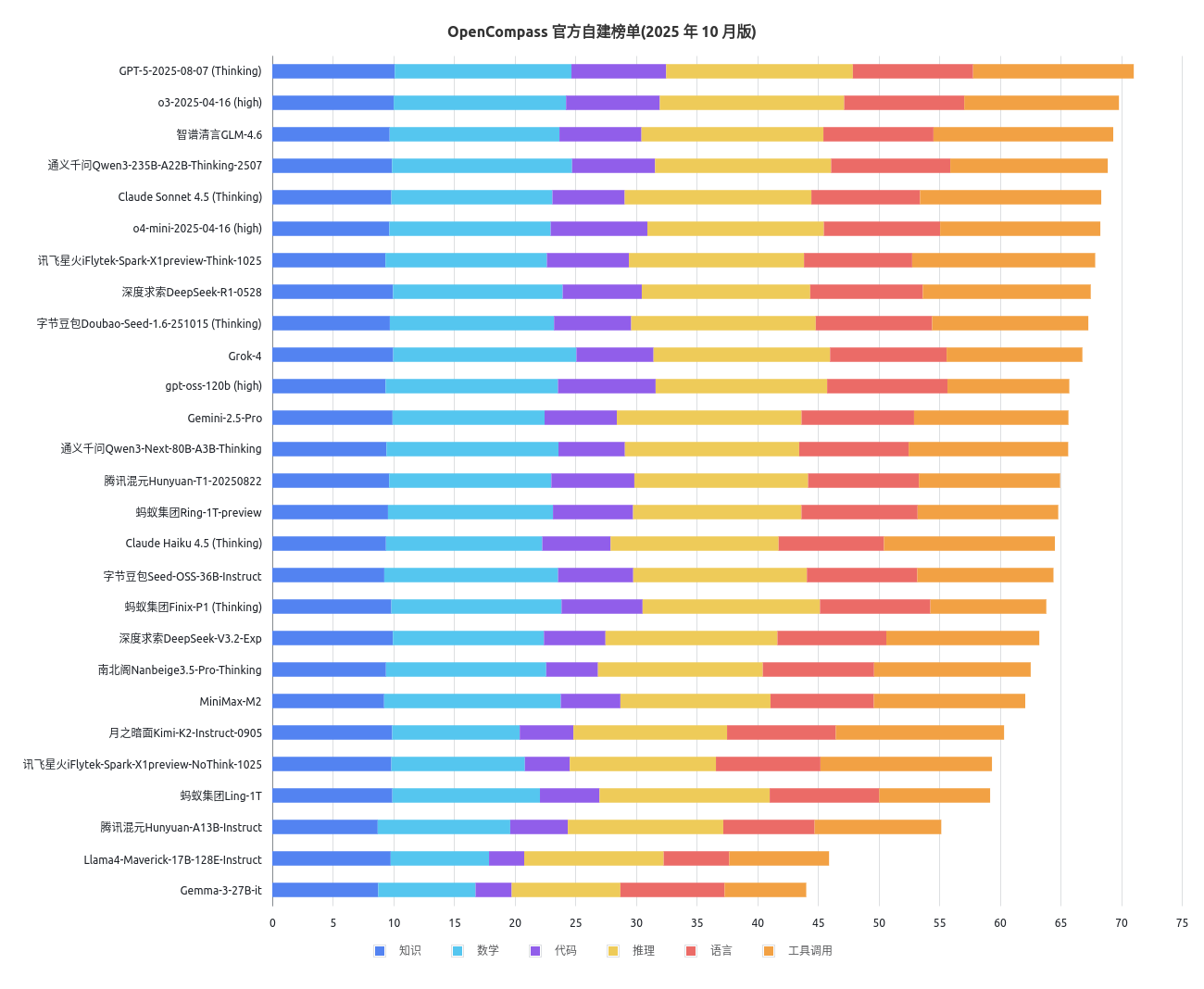
最新榜单概览
综合榜单
子维度榜单
-
语言
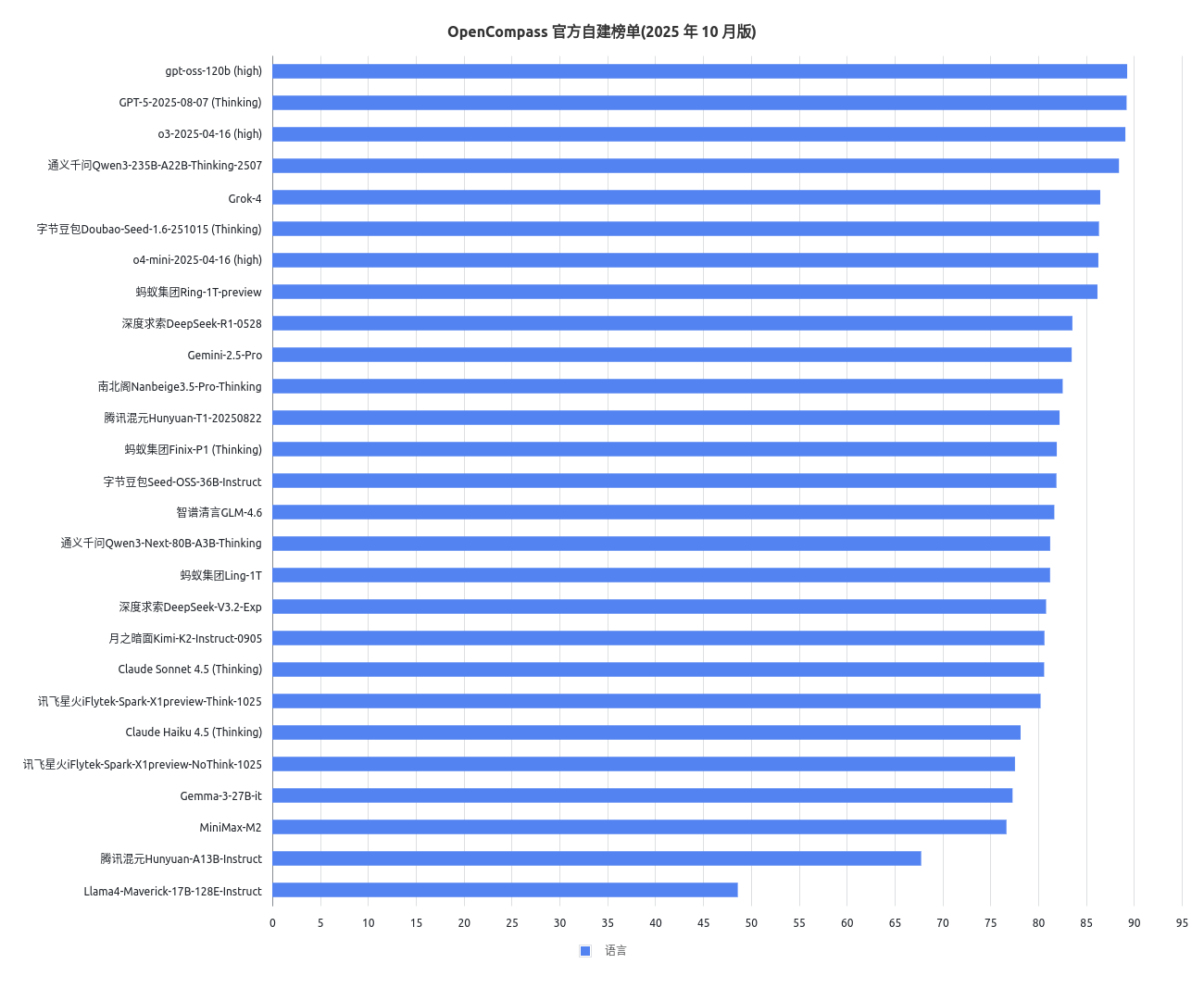
-
推理
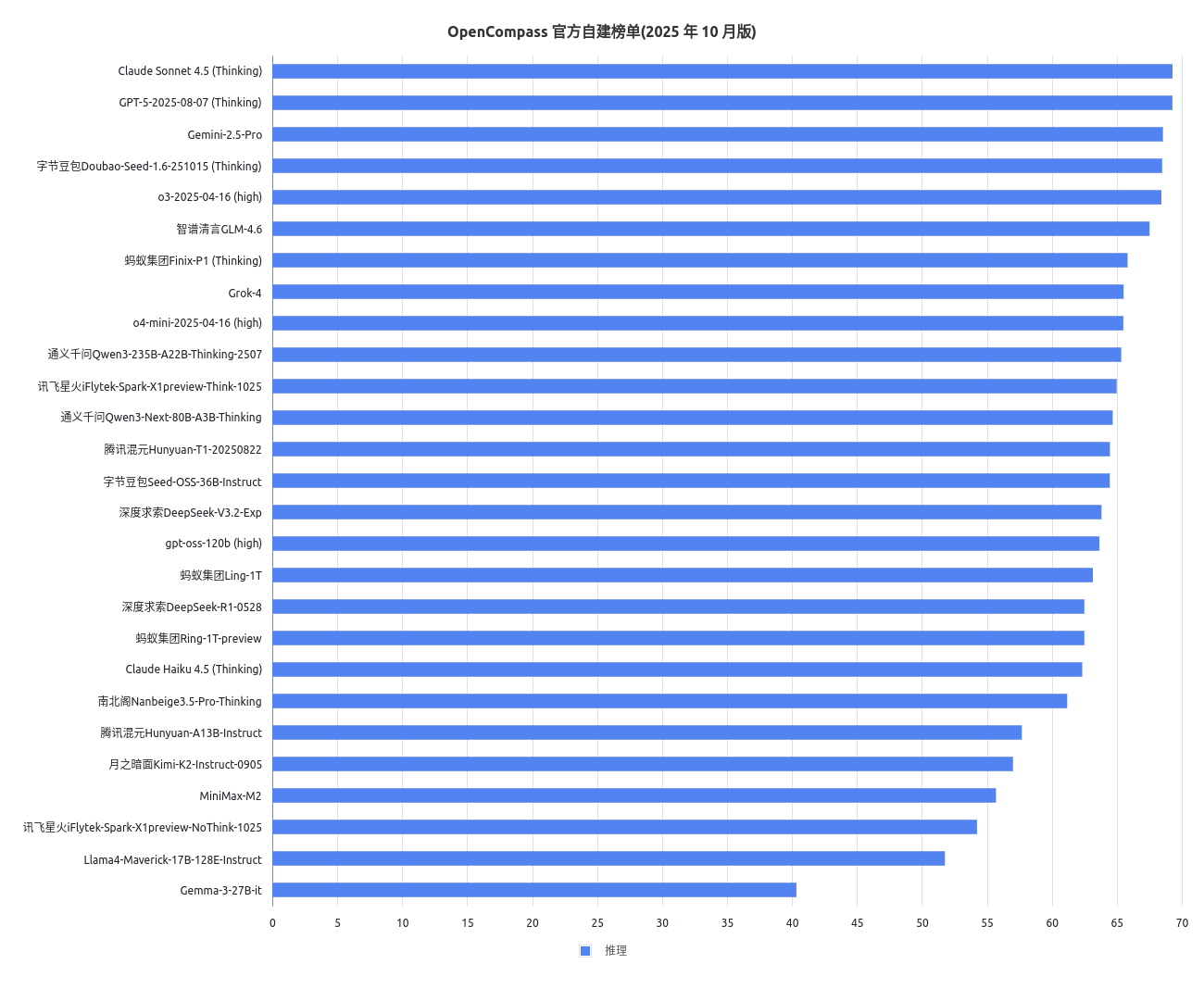
-
知识
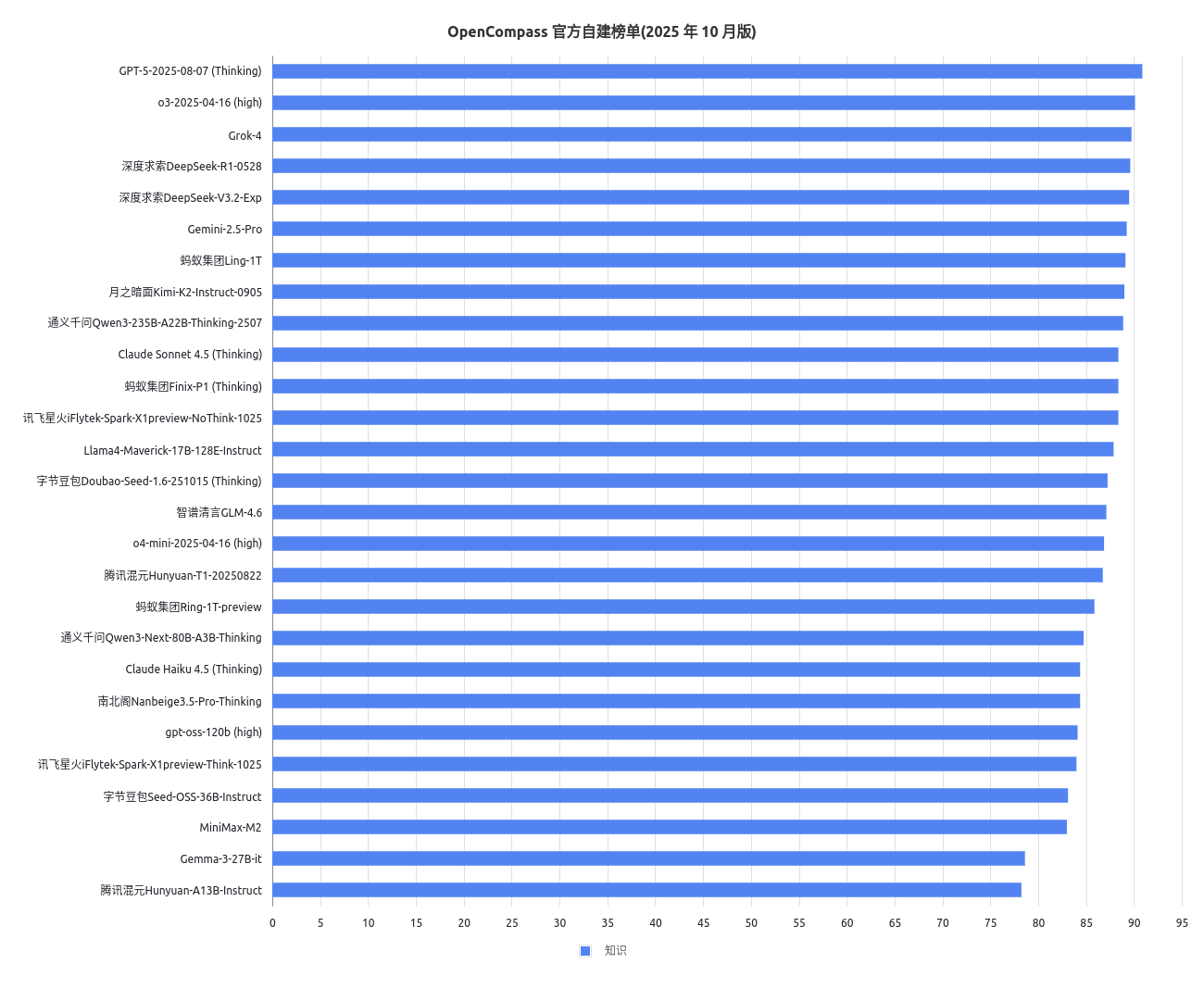
-
代码
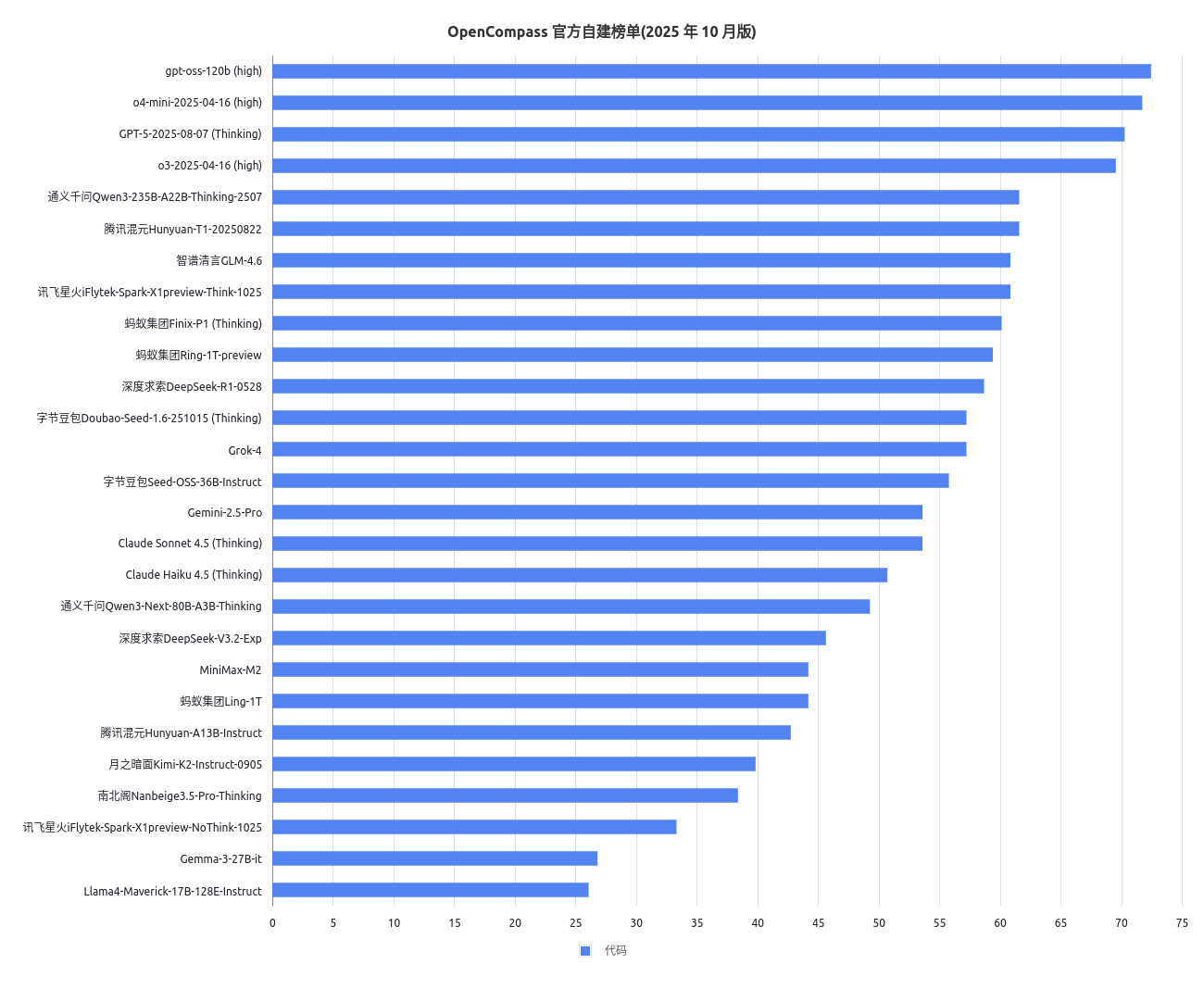
-
数学
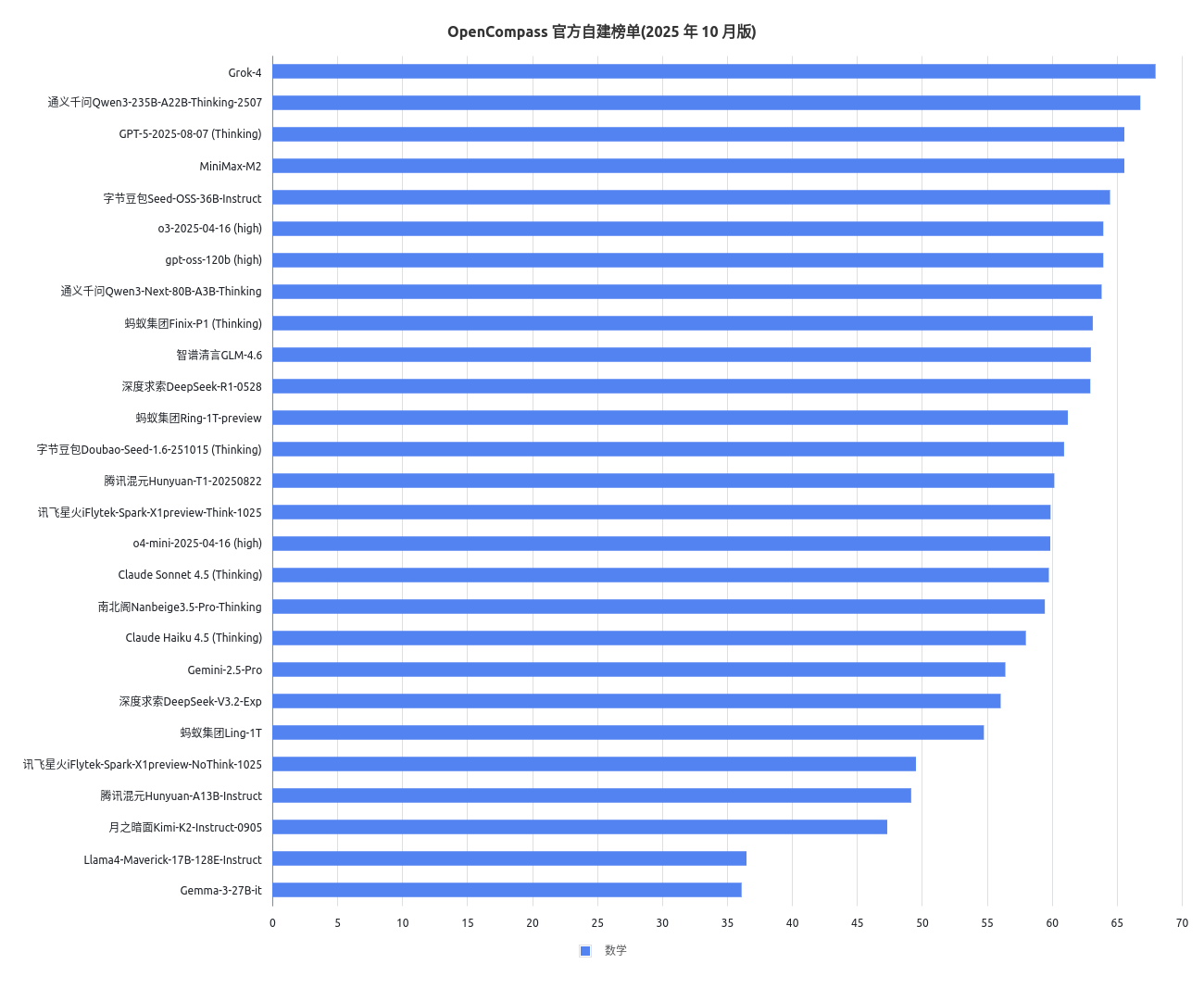
-
工具调用
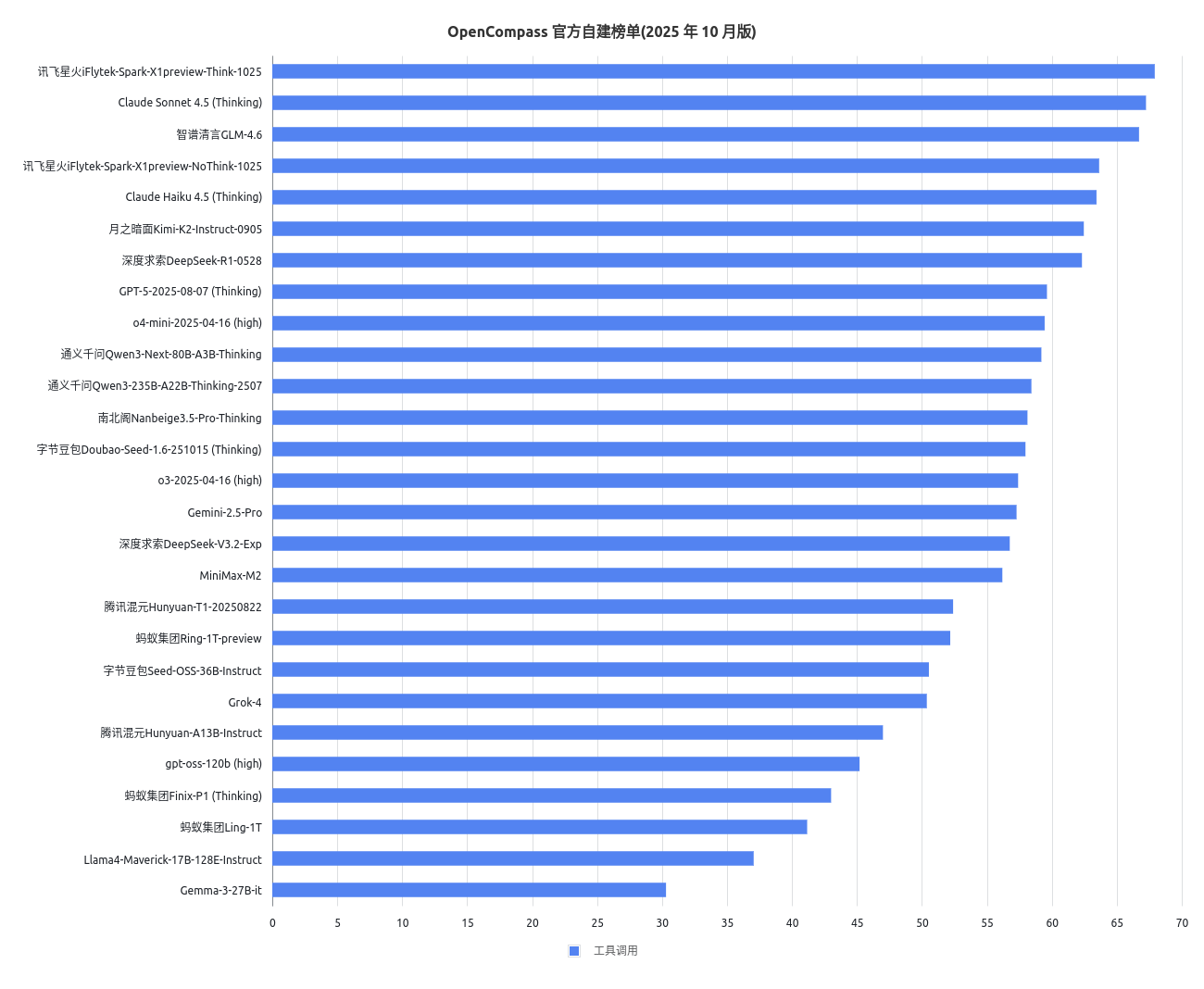
评测题目示例
数学计算
问题:
假设 $a, b, c, d$ 是正实数,满足 $ab^2 + ac^2 \\geq 5bcd$。确定 $\\left(a^2 + b^2 + c^2 + d^2\\right)\\left(\\frac{1}{a^2} + \\frac{1}{b^2} + \\frac{1}{c^2} + \\frac{1}{d^2}\\right)$ 的最小可能值。
标准答案:24GPT-5-2025-08-07 (Thinking) 回复:
\boxed{24}
解法略述:
- 由于目标表达式与约束同为齐次的,令 bc=1,不影响取最小值。设
R = b^2 + c^2 ≥ 2, 以及 t = a/d。由约束 ab^2 + ac^2 ≥ 5bcd 得到 aR ≥ 5d,即 t ≥ 5/R。
- 此时
S = (a^2 + b^2 + c^2 + d^2)(1/a^2 + 1/b^2 + 1/c^2 + 1/d^2)
= (R + a^2 + d^2)(R + 1/a^2 + 1/d^2)
= (R + d^2(t^2+1))(R + (1/d^2)(1+1/t^2)).
- 对固定的 R,t,用 AM-GM 在 d^2 上取最小可得
S ≥ (R + t + 1/t)^2,
且等号当且仅当 d^2 = 1/t(等价于 ad = 1)。
- 现最小化 (R + t + 1/t) 在 R ≥ 2, t ≥ 5/R 上的下界:
- 若 R ≥ 5,则 t+1/t 在 t ≥ 5/R ≤ 1 上的最小值为 2(取 t=1),故 S ≥ (R+2)^2 ≥ 49。
- 若 2 ≤ R ≤ 5,则最小值取在 t = 5/R,得
S ≥ (R + 5/R + R/5)^2。
令 f(R) = (R + 5/R + R/5),在 [2,5] 上最小值由 f'(R)=0 给出 R = 5/√6,此时
f(R) = 2√6,故 S_min = (2√6)^2 = 24。
- 构造取等:取(在 bc=1 归一化下)
a^2 = √6, d^2 = 1/√6, 且令 b,c>0 满足 b^2 + c^2 = 5/√6(例如令 b^2,c^2 为 t^2 - (5/√6)t + 1 = 0 的两根),
则 a(b^2 + c^2) = 5d,且 ad=1,从而 S = 24。Claude Haiku 4.5 (Thinking) 回复(Thinking过程略):
看到这道题,我需要在约束条件 $ab^2 + ac^2 \geq 5bcd$ 下最小化 $(a^2 + b^2 + c^2 + d^2)\left(\frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} + \frac{1}{d^2}\right)$。
## 确定最小值在约束边界上
由Cauchy-Schwarz不等式:
$$(a^2 + b^2 + c^2 + d^2)\left(\frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} + \frac{1}{d^2}\right) \geq 16$$
等号成立当且仅当 $a=b=c=d$。
检验 $a=b=c=d$ 是否满足约束:
- $ab^2 + ac^2 = 2a^3$
- $5bcd = 5a^3$
需要 $2a^3 \geq 5a^3$,即 $2 \geq 5$,矛盾!
所以 $a=b=c=d$ 不在可行域内。设 $\nabla f = 0$ 在无约束情况下会给出 $a=b=c=d$,这在有约束时不可行。
因此最小值必在约束边界上达到:$ab^2 + ac^2 = 5bcd$
## 利用拉格朗日乘数法
记 $S = a^2 + b^2 + c^2 + d^2$ 和 $T = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} + \frac{1}{d^2}$
在边界上建立拉格朗日条件。注意到约束条件中 $b$ 和 $c$ 的对称性,我猜测最优点满足 $b=c$。
## 情况:$b=c$
当 $b=c$ 时,约束变为:
$$2ab^2 = 5b^2d \implies d = \frac{2a}{5}$$
由于目标函数在缩放下为0次齐次,而约束为3次齐次,可设 $a=1$。则 $d = \frac{2}{5}$。
此时:
- $S = 1 + 2b^2 + \frac{4}{25} = \frac{29}{25} + 2b^2$
- $T = 1 + \frac{2}{b^2} + \frac{25}{4} = \frac{29}{4} + \frac{2}{b^2}$
从拉格朗日条件 $2bT - \frac{2S}{b^3} = 0$(这源于约束中 $2ab - 5cd = 0$),得:
$$b^4 T = S$$
代入得:
$$b^4\left(\frac{29}{4} + \frac{2}{b^2}\right) = \frac{29}{25} + 2b^2$$
$$\frac{29b^4}{4} + 2b^2 = \frac{29}{25} + 2b^2$$
$$\frac{29b^4}{4} = \frac{29}{25}$$
$$b^4 = \frac{4}{25} \implies b^2 = \frac{2}{5}$$
## 计算目标函数值
当 $a=1, b=c=\sqrt{\frac{2}{5}}, d=\frac{2}{5}$ 时:
$$S = 1 + \frac{2}{5} + \frac{2}{5} + \frac{4}{25} = 1 + \frac{4}{5} + \frac{4}{25} = \frac{25+20+4}{25} = \frac{49}{25}$$
$$T = 1 + \frac{5}{2} + \frac{5}{2} + \frac{25}{4} = 1 + 5 + \frac{25}{4} = \frac{49}{4}$$
$$f = S \cdot T = \frac{49}{25} \cdot \frac{49}{4} = \frac{2401}{100}$$
## 验证这是最小值
可以验证其他情况(如 $b=c=d$)给出更大的值:
- 当 $b=c=d$ 时:$f = \frac{37}{25} \cdot \frac{79}{4} = \frac{2923}{100} > \frac{2401}{100}$ ✓
因此,最小可能值为 $\boxed{\frac{2401}{100}}-
在该问题的解答过程中,GPT-5-2025-08-07 (Thinking) 模型基于简洁、严密的推理计算正确地解答了问题;而Claude Haiku 4.5 (Thinking) 引入了错误的对称型假设,导致搜索空间被限制,从而找到了一个局部最小值而非全局最优解。
学科推理
问题:
(答案可能不唯一)一定温度下,分别将两种亚硫酸氢盐加热分解,达平衡时的压强分别为 p₁、p₂。
i. NH₄HSO₃(s) ⇌ NH₃(g) + H₂O(g) + SO₂(g) p₁ = a Pa
ii. 2NaHSO₃(s) ⇌ Na₂SO₃(s) + H₂O(g) + SO₂(g) p₂ = b Pa
在该温度下,将一定质量的 NH₄HSO₃与 NaHSO₃加入某密闭容器中,平衡时,三种固体均存在。下列说法不正确的是
A. 平衡时,K₁ = a³/27 Pa³,K₂ = b²/4 Pa²
B. 保持恒温将容器体积压缩,再次平衡时各气体的浓度均减小
C. 保持恒温、恒压,若再通入少量 NH₃,再次平衡时容器内 H₂O 的物质的量不变
D. 保持恒温、恒容,若再通入少量 NH₃,再次平衡时体系的总压强不变
标准答案:BCGLM-4.6回复:
We need to find the incorrect statement(s). The question says "下列说法不正确的是" which likely expects one answer (the incorrect statement). However, it says "答案可能不唯一", meaning there may be multiple correct answers (or multiple incorrect statements). Actually they said "答案可能不唯一", implying that more than one statement could be correct/incorrect? The phrase "不正确的是" could be multiple, but typical Chinese multiple choice single answer: "下列说法不正确的是" (choose the incorrect one). However, they add "答案可能不唯一", so maybe multiple options may be correct (i.e., there are multiple incorrect statements). Let's interpret: The statements A-D; choose those that are incorrect (maybe multiple). Could be a multi-select question where you must select all that are false. So we need to identify which statements are false. The final answer may be something like "B, C" etc. But they require "answers" in a list of strings. But the problem is singular: "Solve the problem step by step. If the problem contains multiple sub-questions, make sure to solve each one individually." This seems to treat each statement as a sub-question perhaps? However "output only the final answers in the following format: {"answers": ["answer to sub-question 1", "answer to sub-question 2", ...]}" The instructions are ambiguous. Usually for a multi-select question, we may provide the list of incorrect statements (maybe a list of letters). So final answer could be like ["B","C"] if B and C are incorrect.
But we need to analyze each statement thoroughly.
First, we need to compute equilibrium constants K1, K2 from the given pressures for each reaction.
......(Thinking过程省略)
But verify that A is correct, D is correct. Let's also double-check D for any nuance: Keep T constant, constant V, add NH3. At equilibrium, the partial pressures are fixed. So total pressure is sum fixed. So indeed after equilibrium total pressure returns to original. So D correct.
Thus answer: B and C are incorrect.
Now confirm that there's no nuance about K1 K2 expression: Are they asking about "平衡时" i.e., at equilibrium when only one solid is present (the separate experiments) the equilibrium constants are K1 = a^3/27 Pa^3, K2 = b^2/4 Pa^2. That is correct.
Now check the sign: Kp has units: For reaction i, Kp has units (Pa)^3, but often we use dimensionless with standard pressure. However they give unit Pa^3. So fine.
Now B: "保持恒温将容器体积压缩,再次平衡时各气体的浓度均减小". Actually concentration is mol per volume. At constant T, after compressing volume, the equilibrium partial pressures remain same (since solids buffer). So concentration = p_i / RT remains same, not decreased. So B false.
Now C: "保持恒温、恒压,若再通入少量 NH₃,再次平衡时容器内 H₂O 的物质的量不变". As argued, not necessarily true, may change. So C false.
Now D: "保持恒温、恒容,若再通入少量 NH₃,再次平衡时体系的总压强不变". True.
Thus answer: B and C are incorrect.
Now we need to output just final answer. Use JSON.
Thus final answer:
```json
{
"answers": [
"B",
"C"
]
}
```Gemini-2.5-Pro回复(Thinking过程略):
Here is a step-by-step solution to the problem.
**Step 1: Analyze the individual equilibria and calculate the equilibrium constants.**
* **Reaction i:** NH₄HSO₃(s) ⇌ NH₃(g) + H₂O(g) + SO₂(g)
* The equilibrium constant in terms of partial pressures is K₁ = p(NH₃) * p(H₂O) * p(SO₂).
* The solid NH₄HSO₃ does not appear in the expression.
* According to the stoichiometry, the moles of the gaseous products are in a 1:1:1 ratio. Therefore, their partial pressures are equal: p(NH₃) = p(H₂O) = p(SO₂).
* The total pressure is p₁ = p(NH₃) + p(H₂O) + p(SO₂).
* Given p₁ = a Pa, we have p(NH₃) = p(H₂O) = p(SO₂) = a/3 Pa.
* Substituting these into the K₁ expression: K₁ = (a/3) * (a/3) * (a/3) = a³/27 Pa³.
* **Reaction ii:** 2NaHSO₃(s) ⇌ Na₂SO₃(s) + H₂O(g) + SO₂(g)
* The equilibrium constant is K₂ = p(H₂O) * p(SO₂).
* The solids NaHSO₃ and Na₂SO₃ do not appear in the expression.
* According to the stoichiometry, the moles of the gaseous products are in a 1:1 ratio. Therefore, their partial pressures are equal: p(H₂O) = p(SO₂).
* The total pressure is p₂ = p(H₂O) + p(SO₂).
* Given p₂ = b Pa, we have p(H₂O) = p(SO₂) = b/2 Pa.
* Substituting these into the K₂ expression: K₂ = (b/2) * (b/2) = b²/4 Pa².
* **Conclusion for Statement A:** The statement "平衡时,K₁ = a³/27 Pa³,K₂ = b²/4 Pa²" is correct.
**Step 2: Analyze the combined equilibrium system.**
When both reactions occur in the same container and reach equilibrium with all three solids (NH₄HSO₃, NaHSO₃, Na₂SO₃) present, both equilibrium conditions must be satisfied simultaneously. Let the partial pressures at this new equilibrium be p'(NH₃), p'(H₂O), and p'(SO₂).
1. K₁ = p'(NH₃) * p'(H₂O) * p'(SO₂) = a³/27
2. K₂ = p'(H₂O) * p'(SO₂) = b²/4
From these two equations, we can determine the partial pressures of each gas at equilibrium.
From equation (2), we have p'(H₂O) * p'(SO₂) = b²/4.
The H₂O and SO₂ gases are produced by both reactions. Let's consider the relationship between their molar amounts.
Moles of H₂O produced = (moles from reaction i) + (moles from reaction ii).
Moles of SO₂ produced = (moles from reaction i) + (moles from reaction ii).
From the stoichiometry of reaction i, moles of H₂O = moles of SO₂ = moles of NH₃.
From the stoichiometry of reaction ii, moles of H₂O = moles of SO₂.
Therefore, the total moles of H₂O must equal the total moles of SO₂ in the gas phase. This means their partial pressures are equal: p'(H₂O) = p'(SO₂).
Substituting this into the K₂ expression: (p'(H₂O))² = b²/4, which gives p'(H₂O) = b/2.
Thus, p'(H₂O) = p'(SO₂) = b/2 Pa.
Now, we can find p'(NH₃) using the K₁ expression:
p'(NH₃) * (b/2) * (b/2) = a³/27
p'(NH₃) * (b²/4) = a³/27
p'(NH₃) = (a³/27) / (b²/4) = 4a³ / (27b²) Pa.
So, at any equilibrium point at this temperature, as long as all three solids are present, the partial pressures of the gases are fixed at these values.
**Step 3: Evaluate the remaining statements.**
* **Statement B:** 保持恒温将容器体积压缩,再次平衡时各气体的浓度均减小 (Keeping T constant, compress the volume. At the new equilibrium, the concentration of each gas decreases).
* When the volume is compressed, the partial pressures of all gases increase instantaneously. This causes the reaction quotients (Q₁ and Q₂) to become greater than the equilibrium constants (K₁ and K₂).
* According to Le Chatelier's principle, both equilibria will shift to the left (the side with fewer moles of gas) to counteract the increase in pressure.
* The system will reach a new equilibrium. Since the temperature is constant and we assume all three solid phases are still present, the equilibrium partial pressures must return to their original, fixed values determined in Step 2.
* p_final(gas) = p_initial(gas).
* Gas concentration is given by the ideal gas law: c = n/V = p/(RT).
* Since the final partial pressure (p), gas constant (R), and temperature (T) are the same as in the initial equilibrium, the final concentration (c) must also be the same as the initial concentration.
* The statement claims the concentrations decrease. This is incorrect; they remain constant. Therefore, statement B is incorrect.
* **Statement C:** 保持恒温、恒压,若再通入少量 NH₃,再次平衡时容器内 H₂O 的物质的量不变 (Keeping T and P constant, if a small amount of NH₃ is added, at the new equilibrium, the amount of substance of H₂O in the container does not change).
* Adding NH₃ increases p(NH₃), causing Q₁ > K₁. Equilibrium (i) shifts left: NH₃(g) + H₂O(g) + SO₂(g) → NH₄HSO₃(s).
* This consumes H₂O and SO₂, causing p(H₂O) and p(SO₂) to drop. This makes Q₂ < K₂. Equilibrium (ii) shifts right: 2NaHSO₃(s) → Na₂SO₃(s) + H₂O(g) + SO₂(g).
* The net effect is that for every mole of added NH₃ consumed by reaction (i), one mole of H₂O and SO₂ are also consumed. To replenish them and restore the partial pressures, reaction (ii) produces one mole of H₂O and SO₂. The shifts are coupled.
* The overall net reaction is: NH₃(g, added) + 2NaHSO₃(s) → NH₄HSO₃(s) + Na₂SO₃(s).
* This net reaction shows that the added NH₃ is consumed by reacting with the solids. The amounts of H₂O(g) and SO₂(g) in the equilibrium gas phase act as intermediaries and their net amounts do not change. The amount of NH₃(g) at equilibrium also returns to its original value.
* Since the number of moles of H₂O gas is unchanged, the statement is correct.
* **Statement D:** 保持恒温、恒容,若再通入少量 NH₃,再次平衡时体系的总压强不变 (Keeping T and V constant, if a small amount of NH₃ is added, at the new equilibrium, the total pressure of the system is unchanged).
* As explained for statement C, when NH₃ is added, the system shifts to consume the added NH₃ and restore the original equilibrium partial pressures of all gases (NH₃, H₂O, SO₂).
* Since the partial pressure of each gas returns to its initial equilibrium value, the total pressure, which is the sum of the partial pressures, must also return to its initial value.
* Therefore, the statement is correct.
**Step 4: Identify the incorrect statement.**
Based on the analysis:
* Statement A is correct.
* Statement B is incorrect.
* Statement C is correct.
* Statement D is correct.
The problem asks for the incorrect statement.
```json
{
"answers": [
"B"
]
}
```-
在该问题的解答过程中,GLM-4.6通过对每个选项的严密分析得出了正确的判断;而Gemini-2.5-Pro对选项C的分析中错误地假设了体积不变或未充分考虑净反应对气体总量的影响,导致分析不全面,得出了错误的结论。
指令跟随
问题:
为一款即将上市的健康管理应用起名,名字需简洁易记,恰好三个字,其中必须包含“健”字。请提出3个具有创意的名字,并围绕名字,为每个名字创作出10个例句。请确保你的例句既能展示出该应用的创新之处,也能反映其对用户的实际价值。
Checklist:
- 名字是否简洁易记并符合三个字的要求?
- 名字是否包含了“健”字,并能与健康管理应用的主题相关联?
- 提出的名字是否具有创意,能吸引目标用户的兴趣和共鸣?
- 例句是否有效展示了应用的创新功能和与用户健康管理需求的契合点?
- 例句是否语言表达流畅,能够清晰传递出应用的实际价值和场景化使用体验?Doubao-Seed-1.6-251015 (Thinking) 回复(Thinking过程略):
### 健康管理应用名称及例句方案
#### 一、应用名称:健伴行
**核心定位**:陪伴式智能健康同行者,以“温暖陪伴+场景化干预”为创新点,让健康管理不再冰冷孤独。
1. 当你加班久坐超过1小时,健伴行会悄悄弹出**AR动画版“3分钟肩颈放松操”**,虚拟教练会实时纠正你的动作角度,僵硬的肌肉瞬间得到舒缓——创新是AR实时交互,价值是碎片化时间高效放松。
2. 健伴行能联动智能体脂秤,自动生成**“周度身体成分彩虹曲线”**,还用拟人化语音提醒:“本周肌肉量涨了0.2kg,比上周多消耗20大卡,继续加油呀!”——创新是智能硬件联动+拟人化反馈,价值是直观感知身体进步。
3. 针对糖尿病前期用户,健伴行设计了**“碳水摄入可视化”功能**:拍照识别食物后,用不同颜色标注升糖指数(GI),红色代表“高GI雷区”,绿色代表“友好选择”,帮你轻松避开“隐形糖坑”——创新是AI食物识别+GI彩虹标注,价值是精准控糖。
4. 当你深夜emo想吃炸鸡时,健伴行会弹出**“健康替代方案”**:推荐“空气炸锅版红薯条”,附上1分钟教程视频,还能一键跳转外卖平台下单低卡食材——创新是即时需求匹配+场景化解决方案,价值是满足口腹之欲不踩坑。
5. 健伴行的**“家庭健康档案”**支持绑定3位家人,爸妈的血压超标时,你会收到“亲情预警”,还能直接预约社区医生上门随访——创新是家庭联动+医疗资源对接,价值是远程守护家人健康。
6. 健伴行的**“运动路线智能规划”**会结合实时天气和附近公园的“负氧离子浓度”,推荐“晨跑最优路线”,还能显示沿途的厕所、饮水点位置——创新是环境数据联动+路线优化,价值是安全舒适运动。
7. 当你连续3天睡眠不足6小时,健伴行会推送**“睡眠修复微课程”**:用“渐进式呼吸法”动画引导,配合白噪音,帮你10分钟快速入睡——创新是睡眠数据驱动的精准干预,价值是改善睡眠质量。
8. 健伴行的**“慢病用药提醒”**不是简单响铃,而是关联“刷牙后”“早餐时”等日常场景,比如:“刚刷完牙?别忘了吃降压药哦~”——创新是场景化记忆锚点,价值是避免漏服药物。
9. 健身新手用健伴行,会获得**“渐进式训练计划”**:从“10分钟入门有氧”到“30分钟力量训练”,每完成一个阶段解锁“健身小勋章”,还能兑换线下瑜伽垫——创新是游戏化成长体系,价值是新手友好型坚持。
10. 每月底健伴行会生成**“我的健康成长手账”**:用漫画形式记录你从“久坐族”到“每日走1万步”的变化,还能分享到朋友圈“晒成就”——创新是个性化内容生成,价值是正向激励。
#### 二、应用名称:健知行
**核心定位**:知识驱动的行动型健康管家,以“科学认知+可落地行动”为创新点,让健康管理告别盲目。
1. 健知行的**“健康知识库”**不是枯燥文章,而是“场景化微课程”:搜索“失眠怎么办”,会推送5分钟动画,教你“睡前10分钟呼吸法”,还能设置每日练习提醒——创新是知识场景化+行动闭环,价值是知识不闲置。
2. 健知行的**“代谢计算器”**通过7天追踪你的饮食、运动、睡眠数据,生成“个性化代谢率曲线”,帮你找到“不饿肚子也能瘦”的 calorie gap——创新是动态数据建模,价值是科学减肥不反弹。
3. 针对高血压用户,健知行会分析**“血压波动与生活习惯的热力图”**:比如“熬夜后血压升高15mmHg”“吃咸食后波动明显”,让你清晰看到“哪些习惯在偷偷升压”——创新是数据关联分析,价值是找到致病根源。
4. 健知行的**“健康知识卡片”**支持“一键生成行动清单”:收藏“春季养生”后,自动提取“每天3杯温水”“每周2次菠菜”等任务,设置每日提醒——创新是知识转行动的自动化,价值是简单可执行。
5. 当你想提高免疫力时,健知行先让你完成**“免疫力风险测试”**(15道题),然后推荐“维生素C+锌”组合,还附上《自然》杂志的相关研究文献——创新是循证医学支撑,价值是避免盲目补营养。
6. 健知行联动智能手环,实时监测**“运动心率区间”**,进入燃脂区间时会提醒:“当前燃脂效率90%,保持这个节奏再跑5分钟!”——创新是实时生理数据指导,价值是运动高效化。
7. 健知行的**“睡眠问题树”**会根据你的数据,画出“入睡困难→睡前刷手机→蓝光刺激”的因果链,推荐“睡前1小时电子设备隔离计划”——创新是问题根源追溯,价值是从本质解决失眠。
8. 职场人士用健知行,能学到**“办公室核心训练”**:用办公椅做臀桥、用键盘托做手腕拉伸,每个动作配1分钟短视频,午休就能学会——创新是职场场景化知识,价值是碎片时间健身。
9. 健知行的**“饮食日记”**会分析你“汉堡餐”的营养比例:“蛋白质15%、脂肪40%、碳水45%,脂肪超标20%”,还会推荐“替换方案”——创新是营养成分动态分析,价值是理性选择食物。
10. 健知行的**“专家问答”**不是文字回复,而是“1对1语音+图文讲解”:问“膝盖疼能跑步吗”,骨科专家会用3分钟语音解释,附上康复训练图——创新是专业内容可视化,价值是易懂的科学指导。
#### 三、应用名称:健悦活
**核心定位**:愉悦导向的健康生活平台,以“游戏化+情绪价值”为创新点,让健康管理不再有压力。
1. 健悦活的**“快乐运动挑战”**是“好友组队种健康树”:每天一起走3000步,树就长高10cm,累计10天兑换线下有机蔬菜礼盒——创新是社交游戏化+实物奖励,价值是快乐坚持运动。
2. 当你情绪低落时,健悦活的**“情绪树洞”**会推送“用户匿名快乐小事”:“今天收到陌生人的微笑”“猫主子主动蹭我啦”,还能生成“快乐语录卡片”保存——创新是情绪共鸣设计,价值是快速治愈坏心情。
3. 健悦活的**“轻食食谱库”**是“地域特色低卡餐”:川味冒菜(用魔芋代替粉条)、粤式清蒸鱼(配柠檬酱汁),每个食谱标注“热量+烹饪时间”——创新是地域口味适配,价值是吃得开心不单调。
4. 健悦活联动智能体重秤,生成**“体重变化趣味动画”**:瘦1kg会出现“小胖子变苗条”的卡通,配上欢快音乐——创新是趣味数据反馈,价值是正向激励减肥。
5. 亲子家庭用健悦活,能玩**“健康知识抢答”**:比如“哪种蔬菜含维生素C最多?”,答对得“家庭健康积分”,兑换亲子绘本——创新是亲子互动设计,价值是全家养成健康习惯。
6. 健悦活的**“睡眠奖励计划”**:连续7天23点前入睡,解锁“睡眠达人”称号,兑换免费冥想课程——创新是目标激励体系,价值是养成早睡习惯。
7. 想尝试新运动?健悦活的**“兴趣匹配”**会根据你的性格(独处/社交)推荐瑜伽或篮球,还能找到附近的“新手社群”——创新是性格适配+社交链接,价值是找到适合的运动。
8. 健悦活的**“健康日记”**支持“照片+贴纸”:拍早餐贴“元气满满”,拍运动贴“燃烧卡路里”,生成月度“健康生活相册”——创新是个性化记录,价值是留存美好瞬间。
9. 压力大时,健悦活的**“5分钟快乐呼吸法”**用“渐变色呼吸动画”(红→蓝)引导,配合海浪声,压力值下降30%——创新是视觉化呼吸引导,价值是快速减压。
10. 健悦活的**“线上健康派对”**每月组织“春日徒步直播”“低卡烘焙大赛”,和同好一起分享快乐,健康不再孤单——创新是主题化社交活动,价值是营造愉悦健康氛围。
三个名字分别从“陪伴温度”“科学知行”“愉悦体验”切入,覆盖不同用户需求,例句既展示了AI、AR、智能硬件联动等创新点,也突出了“碎片化放松”“精准控糖”“快乐坚持”等实际价值,符合健康管理应用的核心诉求。Kimi-K2-Instruct-0905回复:
1. 名字:健刻
例句:
1. 健刻同步手环,刚跑完3公里就把心率曲线推送到手机。
2. 熬夜到两点,健刻弹出“晚睡风险提示”,一键预约明早的补觉计划。
3. 健刻AI营养师扫描午餐,10秒把卡路里拆成红黄绿三色。
4. 爸妈的血压数据实时跳进健刻家庭圈,我立刻收到“异常波动”红点。
5. 健刻把久坐时间折成“生命币”,攒够500枚可兑换线下私教课。
6. 打开健刻“健刻一下”语音按钮,说“肩颈放松”,5分钟跟做GIF动作。
7. 健刻根据睡眠债自动调暗智能家居灯光,帮你提前进入深睡模式。
8. 健刻社区挑战“连续早睡7天”,完成者瓜分品牌方提供的万元奖池。
9. 健刻把医保码、体检报告、跑步记录缝成一张“健康身份证”,就诊时一键亮码。
10. 用健刻“未来10年”预测引擎,减掉2公斤体重可延长预期寿命38天,目标感瞬间拉满。
2. 名字:健伴
例句:
1. 健伴把血糖仪变成聊天小伙伴,超标时它会撒娇:“今天少吃半碗饭,好吗?”
2. 深夜加班,健伴亮起柔光屏保:“起身喝200ml温水,我陪你走2分钟。”
3. 健伴为孕妇定制“周周不同”运动清单,并同步到老公手机,一起完成胎教散步。
4. 健伴AI心理师识别语音低落,3秒内推送呼吸训练并匹配在线志愿者陪聊。
5. 健伴“药盒识别”功能拍下药品,自动拆分量、设闹钟,漏服时弹窗+震动。
6. 健伴用步数生成公益基金,你每走6000步,企业就向山区捐1元营养包。
7. 健伴“健康剧本杀”把每日任务变闯关,连续完成7关可解锁明星语音彩蛋。
8. 健伴接入企业HR系统,员工达成团队运动目标,公司保费次年下调3%。
9. 健伴为慢病患者生成“可视化年报”,让医生在60秒内看懂全年趋势。
10. 健伴支持离线模式,出差到无网络海岛,本地算法依旧能预警心律不齐。
3. 名字:健光
例句:
1. 健光用摄像头测脸血色,30秒给出“今日气色分”,并推荐对应食疗。
2. 健光AR眼镜在超市货架上打绿标,告诉你哪包薯片对血脂最友好。
3. 健光把睡眠深浅绘成“极光”屏保,一眼看懂昨晚哪段被邻居装修声打断。
4. 健光“阳光债”功能追踪每日日照量,不足时推送附近 rooftop 步行路线。
5. 健光为近视儿童设计“20-20-20”护眼游戏,抬头望远即可捕捉AR小精灵。
6. 健光根据城市空气质量,实时生成“户外跑步光感指数”,帮你挑最佳时段。
7. 健光把体检异常项做成“光束”,长度越短代表改善越快,成就感肉眼可见。
8. 健光联动智能戒指,熬夜时屏幕自动切换暖光,降低褪黑素抑制。
9. 健光“光束打卡”让公司同事比拼每日健康积分,排行榜冠军头像自带光环特效。
10. 健光预测模型显示:若每天多喝1杯水,3个月后皮肤光泽度可提升7%,让你直观看见“健光”带来的改变。-
其中,Doubao-Seed-1.6-251015 (Thinking) 的回复表现出清晰的逻辑结构和具有足够深度的内容,整体围绕“健”字展开,具有较强的主题关联性;各例句表达流畅、展示价值明确,十分贴合Checklist中的具体要求。
-
相比之下,Kimi-K2-Instruct-0905的回复较为精简,虽然内容中同样具有创意丰富、表达清晰、主题明确等优点,但未能满足Checklist中的所有要求,例如问题要求名字必须是三个字,但是模型输出的回答中所有的起名均为两个字。
注意事项
-
大语言模型官方自建榜评测榜单每三月更新一次;
-
新模型厂商若想参与该月榜单评测,可在当月25日前发送邮件至opencompass@pjlab.org.cn申请评测申请加入司南OpenCompass月度评测榜单;
-
加入司南OpenCompass评测的结果默认公开;
-
仅支持开源或对外提供API服务商业化模型(内部迭代研发模型暂不支持评测);
-
为了确保公平性,司南通过公开采购的方式获取了商业API服务,其中包括使用硅基流动等服务商API。然而,由于部分API的稳定性问题或敏感词过滤机制,可能会导致某些问题无法获得答案,特此进行说明。
了解更多
最新大语言模型评测榜单已同步上线至司南官网,欢迎大家访问查看更详细的评测数据!
https://rank.opencompass.org.cn/
同时,司南评测体系中大模型评测过程中所用到的工具链均在GitHub开源,诚挚邀请您在学术研究或产品研发过程中使用我们的工具~






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








